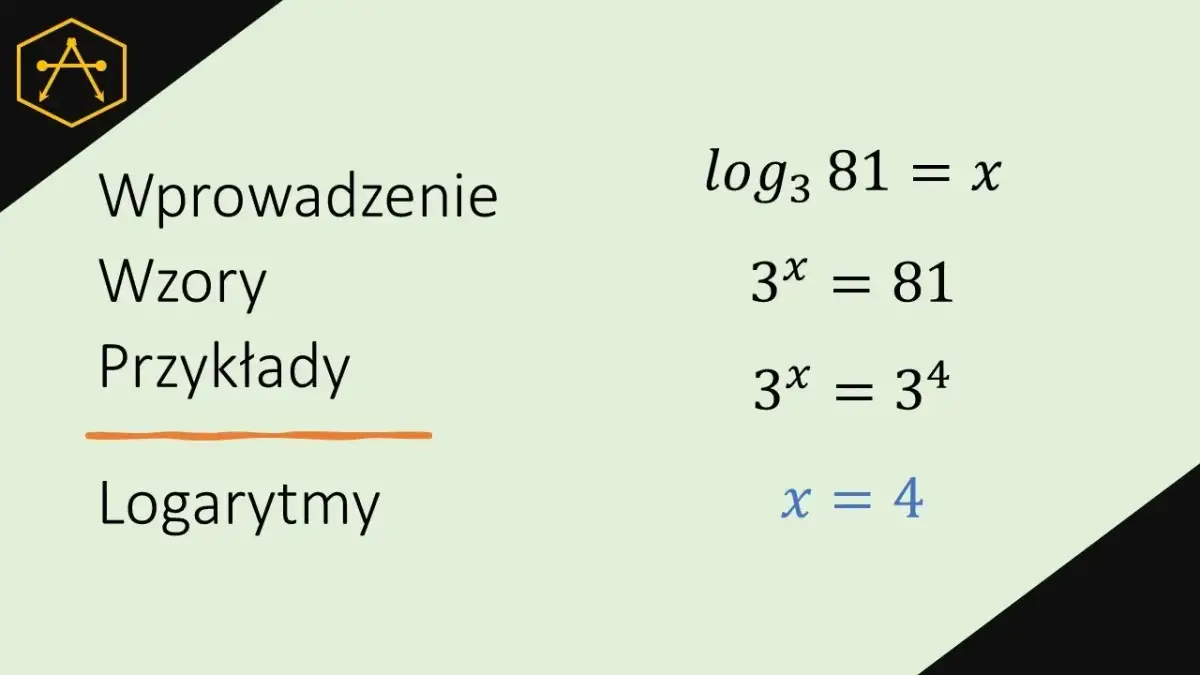Logarytm: Zrozum raz na zawsze! Definicja, wzory, zastosowania w życiu

Ten artykuł w prosty i przystępny sposób wyjaśnia, czym jest logarytm, jak działa i dlaczego jest tak ważny w matematyce i codziennym życiu. Dowiesz się, jak bez trudu rozumieć i obliczać logarytmy, nawet jeśli nie jesteś ekspertem od liczb.

Dlaczego logarytmy są ważne, nawet jeśli nie lubisz matematyki?

Zapewne zastanawiasz się, po co Ci logarytmy, skoro nie planujesz kariery naukowca czy inżyniera. Moje doświadczenie pokazuje, że logarytmy, choć na pierwszy rzut oka wydają się abstrakcyjne, są niezwykle użytecznym narzędziem do opisywania świata. Pomagają nam zrozumieć i mierzyć zjawiska, które nie rosną ani nie maleją w sposób liniowy, ale w postępie geometrycznym.

Pomyśl o tym jak o specjalnym języku, który pozwala nam wyrazić ogromne zakresy wartości w prostszy sposób. Dzięki nim możemy porównywać trzęsienia ziemi o różnej sile, oceniać głośność muzyki czy określać kwasowość roztworów. Bez logarytmów wiele dziedzin nauki i techniki byłoby znacznie trudniejszych do zrozumienia i rozwoju. To właśnie dlatego warto poświęcić chwilę, by je poznać otwierają one oczy na wiele procesów zachodzących wokół nas.

Czym jest logarytm i jak go poprawnie czytać?

Zanim zagłębimy się w szczegóły, spójrzmy na logarytm z szerszej perspektywy. W gruncie rzeczy, logarytm to nic innego jak odwrócenie operacji potęgowania. Jeśli potęgowanie pyta "ile to jest a do potęgi c?", to logarytm pyta "do jakiej potęgi należy podnieść a, żeby otrzymać b?". To klucz do zrozumienia, a kiedy już to "kliknie", reszta staje się znacznie prostsza.

Definicja, która wszystko wyjaśnia: Nierozerwalny związek logarytmu z potęgowaniem

Matematyczna definicja logarytmu jest bardzo precyzyjna i stanowi fundament całej wiedzy na jego temat. Mówimy, że logarytm liczby b przy podstawie a jest równy c (zapisujemy to jako logₐ(b) = c) wtedy i tylko wtedy, gdy a podniesione do potęgi c daje nam liczbę b (czyli aᶜ = b). Ta równoważność jest absolutnie kluczowa. Zauważ, że logarytm jest po prostu wykładnikiem potęgi. Kiedy masz problem z logarytmem, zawsze wracaj do tej definicji, a zobaczysz, że wiele rzeczy się rozjaśni.

Anatomia logarytmu: Kto jest kim w zapisie logₐ(b) = c?

Aby poprawnie operować logarytmami, musimy wiedzieć, co oznaczają poszczególne elementy w zapisie logₐ(b) = c. Każdy z nich ma swoją rolę i spełnia określone warunki:

• a (podstawa logarytmu): To liczba, którą podnosimy do potęgi. Jest to bardzo ważny element, ponieważ od niego zależy wartość logarytmu. Podstawa 'a' musi spełniać dwa warunki: musi być liczbą dodatnią (a > 0) i różną od 1 (a ≠ 1). Dlaczego? Gdyby podstawa była ujemna, mielibyśmy problemy z potęgami (np. (-2) do potęgi 1/2 to pierwiastek z -2, co nie jest liczbą rzeczywistą). Gdyby była równa 1, 1 do dowolnej potęgi zawsze daje 1, więc logarytm byłby niejednoznaczny (np. log₁(5) nie ma sensu).
• b (liczba logarytmowana): To liczba, którą chcemy otrzymać po podniesieniu podstawy 'a' do pewnej potęgi. Liczba logarytmowana 'b' musi być liczbą dodatnią (b > 0). Nie możemy logarytmować liczb ujemnych ani zera, ponieważ nie ma takiej potęgi, do której podniesiona dodatnia podstawa dałaby wynik ujemny lub zero.
• c (wynik logarytmu / wykładnik potęgi): To właśnie ten wykładnik, którego szukamy. Jest to liczba rzeczywista, która może być dodatnia, ujemna lub równa zero.

Pierwsze kroki: Proste przykłady, które pomogą Ci "poczuć" logarytmy

Teoria to jedno, ale nic tak nie pomaga w zrozumieniu, jak praktyka. Przyjrzyjmy się kilku prostym przykładom, które pokażą, jak działa logarytm, odwołując się do definicji:

1. log₂(8) = ? Pytamy: do jakiej potęgi należy podnieść 2, żeby otrzymać 8?

   Wiemy, że 2¹ = 2, 2² = 4, 2³ = 8. Zatem log₂(8) = 3.

2. log₃(9) = ? Pytamy: do jakiej potęgi należy podnieść 3, żeby otrzymać 9?

   Wiemy, że 3¹ = 3, 3² = 9. Zatem log₃(9) = 2.

3. log₅(25) = ? Pytamy: do jakiej potęgi należy podnieść 5, żeby otrzymać 25?

   Wiemy, że 5¹ = 5, 5² = 25. Zatem log₅(25) = 2.

4. log₁₀(100) = ? Pytamy: do jakiej potęgi należy podnieść 10, żeby otrzymać 100?

   Wiemy, że 10¹ = 10, 10² = 100. Zatem log₁₀(100) = 2.

Mam nadzieję, że te przykłady pomogły Ci zobaczyć, że logarytm to po prostu inne spojrzenie na potęgowanie. To naprawdę nie jest takie straszne, prawda?

Poznaj najważniejsze wzory i własności logarytmów

Zrozumienie definicji to pierwszy krok. Kolejnym jest opanowanie podstawowych wzorów i własności logarytmów. To one pozwalają nam upraszczać skomplikowane wyrażenia, rozwiązywać równania i efektywnie pracować z logarytmami. Bez nich, obliczenia byłyby znacznie trudniejsze, a czasem wręcz niemożliwe. Potraktuj je jako swoje matematyczne "skróty", które oszczędzają czas i wysiłek.

Logarytm z iloczynu i ilorazu: Jak sprytnie upraszczać skomplikowane działania?

Jednymi z najbardziej użytecznych wzorów są te dotyczące logarytmu iloczynu i ilorazu. Pozwalają one rozbijać skomplikowane logarytmy na prostsze sumy lub różnice. Logarytm iloczynu mówi, że logₐ(x * y) = logₐ(x) + logₐ(y). Oznacza to, że logarytm z iloczynu dwóch liczb jest równy sumie logarytmów tych liczb. Na przykład, jeśli chcemy obliczyć log₂(16 * 4), możemy to zapisać jako log₂(16) + log₂(4). Wiemy, że log₂(16) = 4 (bo 2⁴ = 16) i log₂(4) = 2 (bo 2² = 4). Zatem log₂(16 * 4) = 4 + 2 = 6. Sprawdźmy: log₂(64) = 6 (bo 2⁶ = 64). Działa!

Podobnie, logarytm ilorazu pozwala nam upraszczać dzielenie. Wzór to logₐ(x / y) = logₐ(x) - logₐ(y). Czyli logarytm z ilorazu dwóch liczb jest równy różnicy logarytmów tych liczb. Weźmy przykład: log₃(81 / 3). Możemy to zapisać jako log₃(81) - log₃(3). Wiemy, że log₃(81) = 4 (bo 3⁴ = 81) i log₃(3) = 1 (bo 3¹ = 3). Zatem log₃(81 / 3) = 4 - 1 = 3. Sprawdźmy: log₃(27) = 3 (bo 3³ = 27). To również się zgadza.

Potęga w logarytmie: Super-moc, która radykalnie ułatwia obliczenia

Kolejny wzór to prawdziwa "super-moc" w obliczeniach logarytmicznych: logₐ(xⁿ) = n * logₐ(x). Mówi on, że jeśli liczba logarytmowana jest podniesiona do potęgi, to ten wykładnik możemy "przenieść" przed logarytm i pomnożyć przez niego. To niezwykle przydatne, gdy mamy do czynienia z dużymi potęgami. Na przykład, zamiast obliczać log₂(64), co już wiemy, że jest 6, możemy to zapisać jako log₂(2⁶). Zgodnie ze wzorem, jest to 6 * log₂(2). A ponieważ log₂(2) = 1, to wynik to 6 * 1 = 6. Widzisz, jak to upraszcza sprawę?

Zmiana podstawy logarytmu: Niezbędne narzędzie w Twoim matematycznym arsenale

Czasami natrafiamy na logarytm o podstawie, której nie potrafimy łatwo obliczyć, albo potrzebujemy przeliczyć logarytm na inną, bardziej dogodną podstawę (np. taką, którą obsługuje nasz kalkulator). Wtedy z pomocą przychodzi wzór na zmianę podstawy logarytmu: logₐ(b) = logₓ(b) / logₓ(a). Ten wzór pozwala nam zmienić podstawę 'a' na dowolną inną podstawę 'x' (oczywiście spełniającą warunki istnienia logarytmu). Na przykład, jeśli chcemy obliczyć log₂(5) za pomocą kalkulatora, który ma tylko logarytmy dziesiętne (log) lub naturalne (ln), możemy to zrobić tak: log₂(5) = log(5) / log(2) lub log₂(5) = ln(5) / ln(2). To naprawdę uniwersalne narzędzie!

Szczególne przypadki, które warto znać na pamięć: logₐ(1) i logₐ(a)

Są dwa szczególne przypadki logarytmów, które warto zapamiętać, ponieważ bardzo często pojawiają się w zadaniach i ułatwiają szybkie obliczenia:

• logₐ(1) = 0: Logarytm z jedynki, niezależnie od podstawy (o ile spełnia warunki a > 0 i a ≠ 1), zawsze wynosi zero. Dlaczego? Ponieważ każda liczba (różna od zera) podniesiona do potęgi zerowej daje 1 (a⁰ = 1). To prosta konsekwencja definicji potęgowania.
• logₐ(a) = 1: Logarytm, w którym liczba logarytmowana jest równa podstawie, zawsze wynosi jeden. To również wynika bezpośrednio z definicji potęgowania: każda liczba podniesiona do potęgi pierwszej daje tę samą liczbę (a¹ = a).

Gdzie logarytmy spotykasz w realnym świecie?

Logarytmy to nie tylko abstrakcyjne równania z podręcznika. Są one głęboko zakorzenione w otaczającym nas świecie i pomagają naukowcom, inżynierom i ekonomistom opisywać i mierzyć różnorodne zjawiska. Od dźwięku, przez światło, po wzrost populacji logarytmy są wszędzie tam, gdzie mamy do czynienia z bardzo szerokim zakresem wartości lub wzrostem wykładniczym.

Od trzęsień ziemi po głośność muzyki: Skala Richtera i decybele

Jednym z najbardziej znanych zastosowań logarytmów jest skala Richtera, używana do mierzenia siły trzęsień ziemi. Jest to skala logarytmiczna, co oznacza, że wzrost o jeden stopień na skali Richtera odpowiada dziesięciokrotnemu wzrostowi amplitudy fal sejsmicznych. Dzięki temu możemy porównywać zarówno słabe wstrząsy, jak i katastrofalne trzęsienia ziemi na jednej, stosunkowo krótkiej skali. Podobnie jest z decybelami (dB), jednostką służącą do pomiaru natężenia dźwięku. Ludzkie ucho reaguje na dźwięk w sposób logarytmiczny to, co dla nas brzmi jak dwukrotnie głośniejszy dźwięk, w rzeczywistości może być dziesięciokrotnie silniejsze. Skala decybelowa pozwala nam wygodnie wyrażać ogromne różnice w natężeniu dźwięku, od szeptu po huk silnika odrzutowego.

Chemia dla ciekawskich: Co logarytm ma wspólnego z kwaśnym smakiem cytryny (skala pH)?

Jeśli kiedykolwiek zastanawiałeś się, dlaczego cytryna jest kwaśna, a mydło zasadowe, to właśnie logarytmy pomagają to opisać! Skala pH, którą chemicy wykorzystują do określania kwasowości lub zasadowości roztworów, jest skalą logarytmiczną. pH to ujemny logarytm dziesiętny ze stężenia jonów wodorowych [H⁺]. Dzięki temu, niewielkie zmiany stężenia jonów wodorowych przekładają się na łatwo mierzalne zmiany na skali pH od 0 do 14. To kolejny przykład, jak logarytmy pozwalają nam radzić sobie z bardzo małymi liczbami w praktyczny sposób.

Niewidzialny silnik postępu: Logarytmy w informatyce, finansach i biologii

Zastosowania logarytmów wykraczają daleko poza chemię czy fizykę. Są one niewidzialnym silnikiem postępu w wielu innych dziedzinach:

• Informatyka: Logarytmy są fundamentalne w analizie złożoności obliczeniowej algorytmów. Mówimy o algorytmach o złożoności O(log n), co oznacza, że czas ich działania rośnie bardzo wolno wraz ze wzrostem danych, co jest kluczowe dla efektywności programów.
• Finanse: W finansach logarytmy są używane do obliczania procentu składanego, stóp zwrotu z inwestycji czy modelowania wzrostu kapitału. Pomagają zrozumieć, jak pieniądze rosną w czasie.
• Biologia: Logarytmy znajdują zastosowanie w modelowaniu wzrostu populacji, rozprzestrzeniania się chorób, a także w analizie danych genetycznych, gdzie często mamy do czynienia z wykładniczymi procesami.

Logarytm dziesiętny (log) a naturalny (ln): kluczowe różnice

Wśród wszystkich możliwych podstaw logarytmów, dwie z nich są szczególnie ważne i spotykamy je najczęściej: podstawa 10 i podstawa 'e'. Mają one swoje specjalne oznaczenia i są wykorzystywane w różnych kontekstach, choć ich fundamentalna zasada działania pozostaje taka sama.

Logarytm dziesiętny: Dlaczego podstawa 10 jest tak uniwersalna?

Logarytm dziesiętny, oznaczany jako log(x) (bez jawnie zapisanej podstawy, co domyślnie oznacza podstawę 10), jest najbardziej intuicyjny dla nas, ponieważ na co dzień posługujemy się systemem dziesiętnym. Jest on powszechnie stosowany w inżynierii, fizyce, chemii (np. w skali pH) i wielu innych dziedzinach, gdzie potrzebujemy pracować z wielkościami rzędu dziesiątek, setek, tysięcy itd. Kalkulatory często domyślnie obliczają logarytm dziesiętny, co świadczy o jego uniwersalności i praktyczności.

Tajemnicza liczba 'e' i logarytm naturalny: Dlaczego jest tak ważny w nauce i przyrodzie?

Obok logarytmu dziesiętnego, równie ważny, a w niektórych dziedzinach nawet ważniejszy, jest logarytm naturalny, oznaczany jako ln(x). Jego podstawą jest tajemnicza liczba Eulera 'e', której przybliżona wartość to e ≈ 2,718. Liczba 'e' jest niezwykle ważną stałą matematyczną, pojawiającą się naturalnie w procesach wzrostu i rozpadu, a także w analizie matematycznej. Logarytm naturalny ma fundamentalne znaczenie w fizyce, ekonomii, biologii i wszędzie tam, gdzie modelujemy procesy ciągłe, takie jak wzrost populacji, rozpad promieniotwórczy czy oprocentowanie ciągłe. Jest to "naturalna" podstawa dla wielu zjawisk w przyrodzie.

Jak unikać najczęstszych błędów przy obliczaniu logarytmów?

Podczas nauki logarytmów, jak w każdej dziedzinie matematyki, łatwo o pomyłki. Z mojego doświadczenia wiem, że pewne błędy powtarzają się częściej niż inne. Świadomość tych pułapek to już połowa sukcesu, dlatego warto im się przyjrzeć, by móc ich skutecznie unikać.

Zapominanie o dziedzinie: Dlaczego nie można logarytmować liczb ujemnych i zera?

To jeden z najczęstszych i najbardziej fundamentalnych błędów. Wielokrotnie podkreślałem, że logarytm ma sens tylko wtedy, gdy podstawa 'a' jest dodatnia i różna od 1 (a > 0, a ≠ 1), a liczba logarytmowana 'b' jest dodatnia (b > 0). Dlaczego to takie ważne? Przypomnij sobie definicję: aᶜ = b. Jeśli 'a' jest dodatnie, to niezależnie od tego, czy 'c' jest dodatnie, ujemne czy zero, wynik 'b' zawsze będzie dodatni. Nigdy nie otrzymamy zera ani liczby ujemnej. Dlatego też, jeśli w zadaniu pojawi się logarytm z liczby ujemnej lub zera, wiedz, że nie ma on rozwiązania w zbiorze liczb rzeczywistych. Zawsze sprawdzaj warunki istnienia logarytmu na początku każdego zadania!

Mylenie wzorów: Kiedy logarytmy dodajemy, a kiedy mnożymy liczby?

Innym powszechnym błędem jest mylenie wzorów, zwłaszcza tych dotyczących iloczynu i sumy. Pamiętaj, że logarytm iloczynu to suma logarytmów (logₐ(x * y) = logₐ(x) + logₐ(y)), a logarytm ilorazu to różnica logarytmów (logₐ(x / y) = logₐ(x) - logₐ(y)). Często widzę, jak uczniowie próbują mnożyć logarytmy, gdy powinni dodawać liczby logarytmowane, lub na odwrót. Zawsze wracaj do podstawowych wzorów i upewnij się, że poprawnie je stosujesz. Ćwiczenie z przykładami, które już omówiliśmy, pomoże Ci utrwalić te zależności.

Przeczytaj również: Potęgi w matematyce: Opanuj zasady i unikaj typowych błędów

Błędne założenia dotyczące podstawy logarytmu czego musisz pilnować?

Ostatni, ale równie ważny błąd, to nieprawidłowe interpretowanie lub pomijanie podstawy logarytmu. Jeśli podstawa nie jest jawnie zapisana (np. log(x)), domyślnie przyjmujemy, że jest to logarytm dziesiętny (podstawa 10). W przypadku ln(x) zawsze chodzi o podstawę 'e'. Nigdy nie zakładaj, że podstawa jest inna, niż wynika to z zapisu lub kontekstu. Upewnij się również, że podstawa zawsze spełnia warunki: jest dodatnia i różna od 1. Dokładność w tym aspekcie jest kluczowa dla poprawnych obliczeń.