Czym jest różnica w matematyce? Zrozum odejmowanie bez trudu!

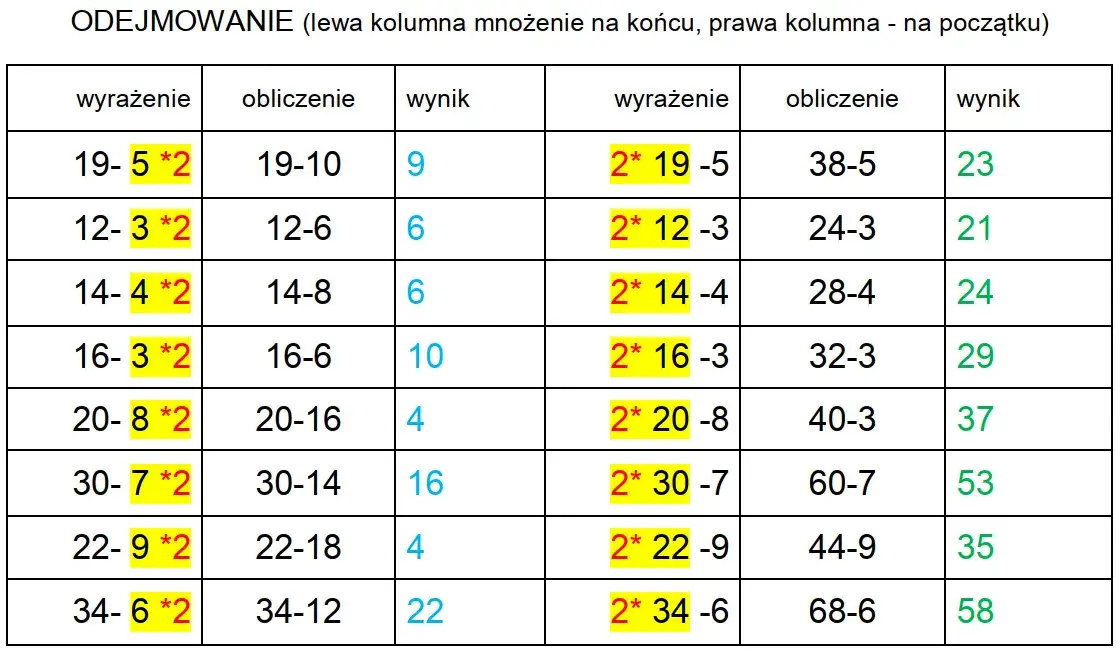
Zrozumienie pojęcia "różnica" w matematyce to absolutna podstawa, bez której trudno ruszyć dalej. Niezależnie od tego, czy jesteś uczniem, rodzicem pomagającym w nauce, czy po prostu chcesz odświeżyć swoją wiedzę, opanowanie tego kluczowego terminu jest niezbędne. Pozwala ono nie tylko poprawnie wykonywać odejmowanie, ale także rozumieć i rozwiązywać wiele codziennych problemów oraz bardziej złożonych zadań matematycznych.

Czym jest różnica w matematyce? Fundament, który musisz poznać

W matematyce różnica to nic innego jak wynik działania odejmowania jednej liczby od drugiej. To jedno z najbardziej fundamentalnych pojęć, które poznajemy na początku naszej przygody z liczbami. Bez jego solidnego zrozumienia trudno jest budować dalszą wiedzę, ponieważ odejmowanie jest wszechobecne w wielu dziedzinach matematyki i życia codziennego.

Odjemna, odjemnik, różnica: poznaj kluczowe pojęcia i ich role

Aby poprawnie mówić o odejmowaniu, musimy znać trzy kluczowe terminy. Liczba, od której odejmujemy, to odjemna. Liczba, którą odejmujemy, nazywa się odjemnikiem. Natomiast wynik tego działania to właśnie różnica. Weźmy prosty przykład: w działaniu 10 - 4 = 6, liczba 10 jest odjemną, 4 to odjemnik, a 6 to różnica. Zawsze warto mieć te role na uwadze, zwłaszcza przy bardziej skomplikowanych obliczeniach.

Dlaczego "oblicz różnicę" to to samo co "odejmij"?

Bardzo często spotykam się z pytaniem, czy "oblicz różnicę" to to samo co "odejmij". Odpowiedź jest prosta: tak, to są synonimy w kontekście matematyki! Kiedy nauczyciel prosi o obliczenie różnicy dwóch liczb, zawsze oznacza to, że należy wykonać działanie odejmowania. Nie ma tu żadnej pułapki ani ukrytego znaczenia po prostu dwie różne formy wyrażenia tej samej operacji.

Jak bezbłędnie obliczać różnicę liczb? Praktyczny przewodnik

Przejdźmy teraz do sedna, czyli do praktycznego obliczania różnicy. Choć wydaje się to proste, diabeł tkwi w szczegółach, a prawidłowe wykonanie działania jest kluczem do uzyskania poprawnego wyniku. Pamiętajmy, że precyzja w matematyce to podstawa.

Złota zasada: dlaczego kolejność w odejmowaniu ma ogromne znaczenie?

Jedną z najważniejszych rzeczy, którą musisz zapamiętać, jest to, że kolejność liczb w odejmowaniu ma fundamentalne znaczenie. Odejmowanie, w przeciwieństwie do dodawania, nie jest przemienne. Oznacza to, że zmiana kolejności odjemnej i odjemnika całkowicie zmienia wynik. Spójrzmy na przykłady:

• Jeśli obliczymy różnicę 8 - 3, otrzymamy 5.
• Ale jeśli zmienimy kolejność i spróbujemy obliczyć 3 - 8, wynik będzie zupełnie inny: -5.

Przykłady, które zrozumie każdy: obliczanie różnicy liczb dodatnich

Aby utrwalić sobie to pojęcie, przejdźmy przez kilka prostych przykładów obliczania różnicy liczb dodatnich:

1. Oblicz różnicę liczb 7 i 2: 7 - 2 = 5
2. Oblicz różnicę liczb 15 i 6: 15 - 6 = 9
3. Oblicz różnicę liczb 23 i 10: 23 - 10 = 13

W każdym z tych przypadków odjemna jest większa od odjemnika, co daje nam dodatni wynik.

Co się dzieje, gdy odejmujemy większą liczbę od mniejszej? Wprowadzenie do liczb ujemnych

Co jednak, gdy odjemnik jest większy od odjemnej? W takim przypadku wkraczamy w świat liczb ujemnych. Wynikiem odejmowania mniejszej liczby od większej będzie liczba ujemna. To ważne rozszerzenie naszego rozumienia różnicy. Na przykład, jeśli obliczymy 5 - 8, otrzymamy -3. To pokazuje, że różnica nie zawsze musi być liczbą dodatnią.

Różnica, gdy liczby są takie same: magiczne zero

Jest jeszcze jeden szczególny przypadek, który warto znać. Jeśli odjemna i odjemnik są identyczne, czyli odejmujemy liczbę od niej samej, różnica zawsze wynosi zero. To logiczne, bo nie ma żadnej "odległości" między dwoma identycznymi wartościami. Prosty przykład: 9 - 9 = 0.

Różnica w zadaniach tekstowych: jak ją rozpoznać i poprawnie zastosować?

Zadania tekstowe to często prawdziwe wyzwanie, ale zrozumienie, kiedy należy obliczyć różnicę, znacząco ułatwia ich rozwiązywanie. Kluczem jest prawidłowa interpretacja treści i wyłapanie słów kluczowych.

"O ile więcej?", "O ile mniej?": słowa klucze, które wskazują na odejmowanie

W zadaniach tekstowych istnieją pewne słowa i zwroty, które niemal zawsze wskazują na konieczność obliczenia różnicy. Oto najpopularniejsze z nich:

• "O ile więcej?" zawsze oznacza odejmowanie, aby znaleźć nadwyżkę.
• "O ile mniej?" również wskazuje na odejmowanie, aby znaleźć niedobór.
• "Różnica wieku" klasyczne zastosowanie różnicy.
• "Różnica cen" porównywanie wartości.
• "Jaka jest różnica między..." bezpośrednie pytanie o różnicę.

Gdy tylko zobaczysz te sformułowania, wiedz, że musisz użyć odejmowania!

Analiza typowych zadań ze szkoły podstawowej

Przeanalizujmy kilka typowych zadań, z którymi spotykają się uczniowie, aby zobaczyć, jak zastosować pojęcie różnicy:

1. Zadanie: Ania ma 12 kredek, a Bartek ma 7 kredek. O ile więcej kredek ma Ania niż Bartek?
   Rozwiązanie: Aby dowiedzieć się, o ile więcej, musimy obliczyć różnicę: 12 - 7 = 5. Ania ma o 5 kredek więcej.
2. Zadanie: W sklepie jabłka kosztują 4 zł za kilogram, a gruszki 6 zł za kilogram. Jaka jest różnica w cenie między gruszkami a jabłkami?
   Rozwiązanie: Obliczamy różnicę: 6 - 4 = 2. Różnica w cenie wynosi 2 zł.
3. Zadanie: Mama ma 35 lat, a tata 38 lat. O ile lat mama jest młodsza od taty?
   Rozwiązanie: Aby znaleźć różnicę wieku, odejmujemy: 38 - 35 = 3. Mama jest młodsza od taty o 3 lata.

Jak uniknąć pomyłki? Prosty sposób na ustalenie, co od czego odjąć

Najczęstszym błędem w zadaniach tekstowych jest zamiana kolejności liczb. Aby tego uniknąć, zawsze zadaj sobie pytanie: "Od której liczby odejmuję, aby uzyskać sensowny wynik w kontekście zadania?". Zazwyczaj odejmujemy mniejszą wartość od większej, gdy szukamy "o ile więcej/mniej" w kontekście dodatnim. Jeśli jednak pytanie dotyczy zmiany (np. "o ile spadła temperatura"), to kolejność może być inna. Kluczowe jest czytanie ze zrozumieniem i wyobrażenie sobie sytuacji.

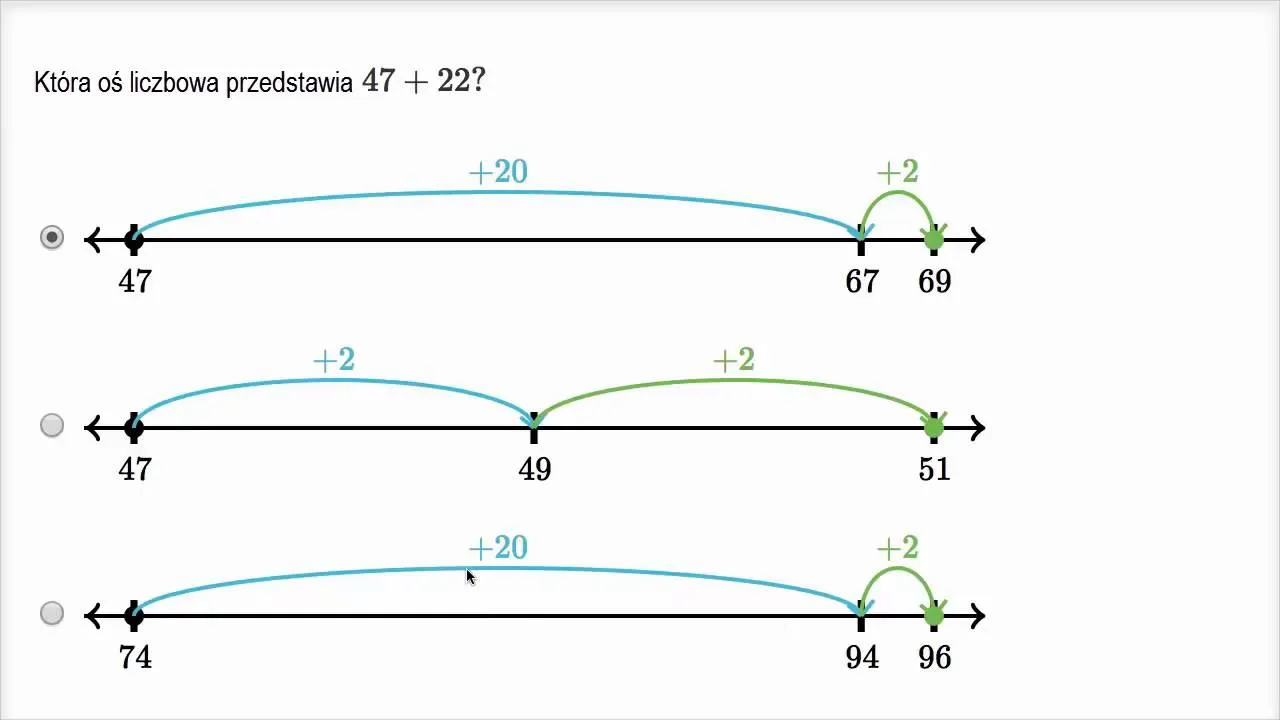
Wizualizacja, która ułatwia zrozumienie: różnica na osi liczbowej

Dla wielu osób, zwłaszcza tych, które są wzrokowcami, wizualizacja jest nieocenionym narzędziem. Przedstawienie różnicy na osi liczbowej może pomóc w lepszym zrozumieniu tego abstrakcyjnego pojęcia.

Jak zobaczyć różnicę? Graficzne przedstawienie odejmowania

Wyobraź sobie oś liczbową. Każda liczba ma na niej swoje miejsce. Kiedy odejmujemy jedną liczbę od drugiej, możemy to zobaczyć jako "przejście" od odjemnej do odjemnika lub jako odległość między tymi dwoma punktami. Na przykład, aby obliczyć 7 - 3, znajdujemy 7 na osi, a następnie "cofamy się" o 3 jednostki. Miejsce, w którym lądujemy (4), to nasza różnica.

Odległość między punktami jako klucz do zrozumienia różnicy

Koncepcja różnicy jako odległości jest niezwykle intuicyjna. Jeśli masz na osi liczbowej punkt 7 i punkt 3, to różnica między nimi to po prostu liczba jednostek, które je dzielą. W tym przypadku odległość wynosi 4 jednostki. To bardzo pomaga zrozumieć, dlaczego 7 - 3 = 4. Ta wizualizacja jest szczególnie przydatna, gdy zaczynamy wprowadzać liczby ujemne, ponieważ pomaga zrozumieć, dlaczego np. różnica między -2 a 3 to 5 jednostek (3 - (-2) = 5).

Najczęstsze pułapki i błędy: sprawdź, czy ich nie popełniasz

Nawet w tak podstawowym działaniu jak odejmowanie, łatwo o pomyłki. Przyjrzyjmy się najczęstszym pułapkom, abyś mógł ich świadomie unikać.

Mylenie odjemnej z odjemnikiem: klasyczny błąd i jak go unikać

Jak już wspomniałem, zamiana odjemnej z odjemnikiem to jeden z najczęstszych błędów. Pamiętaj, że odjemna zawsze stoi na pierwszym miejscu, a odjemnik na drugim. Prosta wskazówka, którą często daję moim uczniom, to myślenie o "odejmowaniu od czegoś". To "coś" to zawsze odjemna. Na przykład, "odejmij 3 od 8" oznacza 8 - 3, nie 3 - 8.

Problemy z interpretacją poleceń w zadaniach tekstowych

Kolejnym źródłem błędów jest niedokładne czytanie zadań tekstowych. Pośpiech i brak skupienia na słowach kluczowych, takich jak "o ile więcej" czy "o ile mniej", prowadzą do błędnej interpretacji i w konsekwencji do złego działania. Zawsze poświęć chwilę na dokładne przeczytanie i zrozumienie, o co tak naprawdę pyta zadanie.

Czy różnica zawsze musi być liczbą dodatnią? Ostateczne wyjaśnienie

Wielu początkujących uczniów zakłada, że różnica zawsze musi być liczbą dodatnią. To nieprawda! Jak już widzieliśmy, różnica może być:

• Dodatnia (gdy odjemna jest większa od odjemnika, np. 10 - 4 = 6).
• Ujemna (gdy odjemnik jest większy od odjemnej, np. 4 - 10 = -6).
• Równa zero (gdy odjemna i odjemnik są identyczne, np. 7 - 7 = 0).

Dlaczego zrozumienie różnicy jest kluczowe w dalszej nauce matematyki?

Może się wydawać, że różnica to tylko proste odejmowanie, ale jej solidne zrozumienie jest absolutnie kluczowe dla całej przyszłej edukacji matematycznej. To fundament, na którym buduje się znacznie bardziej złożone koncepcje.

Od prostego odejmowania do bardziej złożonych działów matematyki

Różnica to nie tylko podstawowe działanie arytmetyczne. Jest ona podstawą dla wielu zaawansowanych pojęć. W algebrze będziesz pracować z różnicami wyrażeń, w analizie funkcji będziesz badać różnice wartości funkcji, a w statystyce obliczać odchylenia, które są niczym innym jak różnicami. Bez pewności w odejmowaniu, te działy matematyki staną się znacznie trudniejsze do opanowania.

Przeczytaj również: Sinus: Co to jest? Zrozum funkcję od trójkąta po GPS!

Różnica jako podstawa do porównywania i analizy danych w codziennym życiu

Poza matematyką szkolną, pojęcie różnicy jest nieustannie wykorzystywane w życiu codziennym do porównywania i analizy danych. Myślę, że każdy z nas robi to niemal automatycznie. Na przykład, gdy porównujemy:

• Różnice w cenach produktów w sklepie.
• Różnice temperatur w prognozie pogody.
• Różnice wieku między członkami rodziny.
• Różnice w wynikach sportowych drużyn.