Szybko i bezbłędnie: jak obliczyć pole trójkąta, znając podstawę, boki lub współrzędne
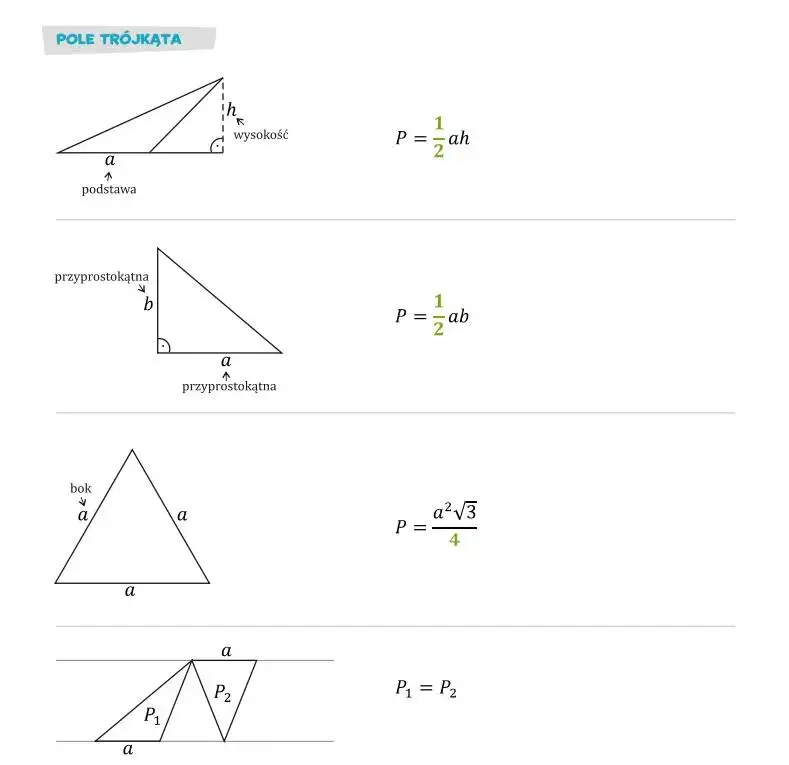
- Podstawowy wzór na pole trójkąta to P = (a * h) / 2, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.
- Dla trójkąta prostokątnego pole obliczysz wzorem P = (a * b) / 2, gdzie 'a' i 'b' to długości przyprostokątnych.
- Pole trójkąta równobocznego można wyliczyć, znając tylko długość boku 'a', używając wzoru P = (a²√3) / 4.
- Gdy nie znasz wysokości, możesz skorzystać ze wzoru Herona (jeśli znasz wszystkie 3 boki) lub wzoru trygonometrycznego (jeśli znasz 2 boki i kąt między nimi).
- Istnieje również metoda obliczania pola z współrzędnych wierzchołków, przydatna w geometrii analitycznej.
- Pamiętaj o prawidłowym wyznaczaniu wysokości (szczególnie w trójkątach rozwartokątnych) i wybieraj odpowiedni wzór do typu trójkąta.
Obliczanie pola trójkąta: uniwersalny wzór, który działa zawsze
Zacznijmy od fundamentów. Najbardziej uniwersalny i najczęściej stosowany wzór na pole trójkąta opiera się na znajomości jego podstawy i wysokości. To absolutna podstawa, którą musisz opanować, zanim przejdziesz do bardziej złożonych przypadków. Właśnie od tego zaczynamy moją przygodę z geometrią i jestem pewien, że Ty też szybko to zrozumiesz.
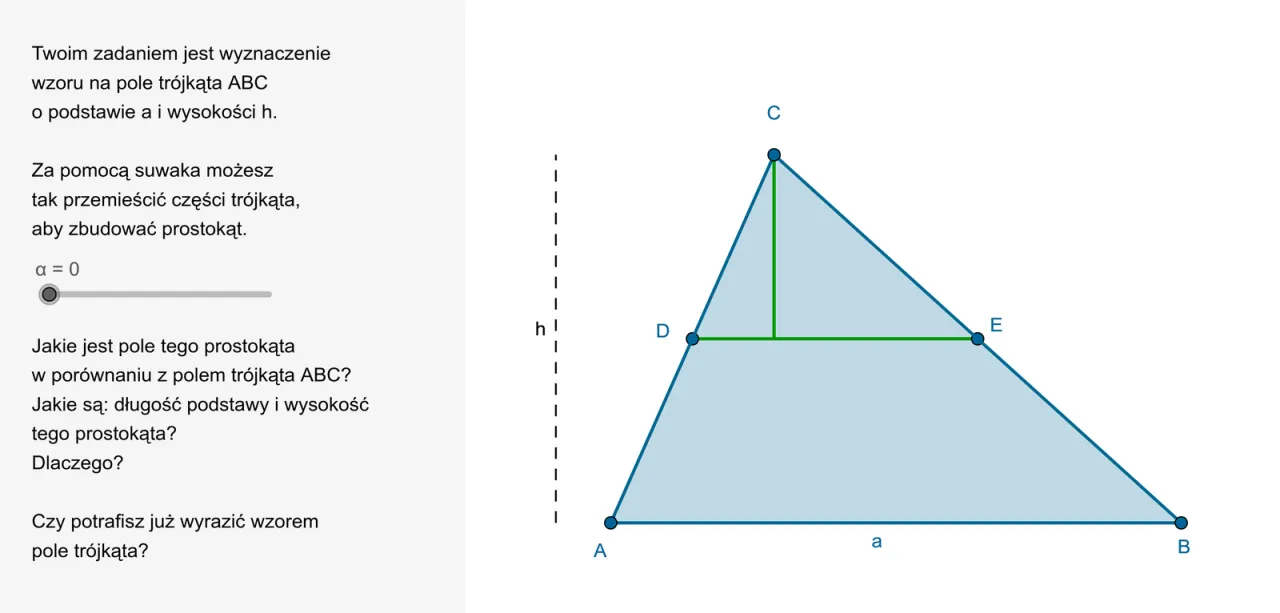
Czym jest podstawa i wysokość, czyli klucz do zrozumienia wzoru
Aby poprawnie obliczyć pole trójkąta, musimy zrozumieć dwa kluczowe pojęcia: podstawę i wysokość. Podstawa to po prostu jeden z boków trójkąta, który wybieramy do obliczeń. Wysokość natomiast to odcinek, który wychodzi z wierzchołka leżącego naprzeciwko wybranej podstawy i opada na nią (lub jej przedłużenie) pod kątem prostym, czyli 90 stopni. To bardzo ważne wysokość zawsze musi być prostopadła do podstawy. Bez tego ani rusz!
Wzór P = 1/2 * a * h w praktyce: Obliczamy pole krok po kroku na przykładzie
Uniwersalny wzór na pole trójkąta to P = (a * h) / 2, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę. Możesz go zapisać również jako P = 1/2 * a * h. Jest prosty i intuicyjny. Zobaczmy, jak to działa na konkretnym przykładzie.
- Dane: Mamy trójkąt, którego podstawa 'a' wynosi 10 cm, a wysokość 'h' opuszczona na tę podstawę wynosi 5 cm.
- Wzór: P = (a * h) / 2
- Podstawienie wartości: P = (10 cm * 5 cm) / 2
- Obliczenia: P = 50 cm² / 2
- Wynik: P = 25 cm².
Jak widać, to naprawdę nic skomplikowanego. Wystarczy znać te dwie wartości i podstawić je do wzoru.
Uwaga na trójkąty rozwartokątne! Gdzie w ich przypadku leży wysokość?
Tutaj pojawia się częsta pułapka, z którą sam się zmagałem, gdy byłem uczniem. W trójkątach rozwartokątnych (czyli takich, które mają jeden kąt większy niż 90 stopni) wysokość opuszczona na jeden z boków może znajdować się poza trójkątem. W takiej sytuacji musimy przedłużyć podstawę, aby wysokość mogła na nią prostopadle opaść. Pamiętaj, że długość podstawy nadal mierzymy tylko w obrębie trójkąta, a przedłużenie służy jedynie do wyznaczenia miejsca, gdzie wysokość "spotka" linię podstawy. To kluczowe, aby nie popełnić błędu!
Trójkąt prostokątny: obliczanie pola jest prostsze niż myślisz
Trójkąt prostokątny to prawdziwy ulubieniec wielu uczniów, jeśli chodzi o obliczanie pola. Dlaczego? Ponieważ jego specyficzna budowa sprawia, że obliczenia stają się znacznie prostsze. Nie musimy szukać żadnej dodatkowej wysokości, co jest ogromnym ułatwieniem. Z mojego doświadczenia wiem, że to właśnie ten typ trójkąta najczęściej pojawia się w zadaniach na początku nauki.
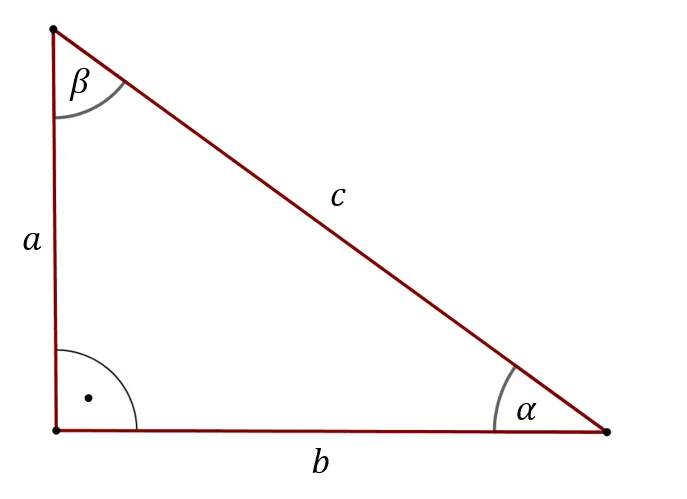
Dlaczego przyprostokątne są Twoimi najlepszymi przyjaciółmi?
W trójkącie prostokątnym mamy dwa boki, które tworzą kąt prosty nazywamy je przyprostokątnymi. Trzeci bok, leżący naprzeciwko kąta prostego, to przeciwprostokątna. I tu tkwi cała magia: jedna z przyprostokątnych może pełnić rolę podstawy, a druga rolę wysokości! Ponieważ są one do siebie prostopadłe, spełniają idealnie warunek wysokości opadającej pod kątem prostym na podstawę. To sprawia, że wzór na pole staje się niezwykle intuicyjny.Błyskawiczne obliczenia: Zastosowanie wzoru P = 1/2 * a * b w zadaniu
Dla trójkąta prostokątnego wzór na pole to P = (a * b) / 2, gdzie 'a' i 'b' to długości przyprostokątnych. To nic innego jak podstawowy wzór, tylko że 'h' zostało zastąpione przez drugą przyprostokątną. Spójrzmy na przykład:
Mamy trójkąt prostokątny, którego przyprostokątne mają długości 6 cm i 8 cm. P = (6 cm * 8 cm) / 2 P = 48 cm² / 2 P = 24 cm².
Proste, prawda? Wystarczy zidentyfikować przyprostokątne i gotowe.

Pole trójkąta równobocznego: bez wysokości, tylko z długością boku
Trójkąt równoboczny to kolejny szczególny przypadek, który ma swój własny, bardzo wygodny wzór na pole. Jego unikalne właściwości pozwalają nam pominąć konieczność obliczania wysokości, co jest sporym ułatwieniem, zwłaszcza gdy wysokość jest liczbą niewymierną. To jeden z tych wzorów, które po prostu warto zapamiętać, bo oszczędza mnóstwo czasu.
Jeden bok, jeden wzór: Odkryj moc wzoru P = (a²√3) / 4
Trójkąt równoboczny to trójkąt, który ma wszystkie boki równej długości i wszystkie kąty równe 60 stopni. Dzięki tej symetrii możemy użyć specjalnego wzoru, który wymaga znajomości tylko długości jednego boku (oznaczmy go jako 'a'). Wzór ten to P = (a²√3) / 4. Jest on niezwykle wygodny, ponieważ nie musisz w ogóle zajmować się wysokością, która w trójkącie równobocznym wynosi h = (a√3) / 2. Wzór na pole już zawiera w sobie ten element, co jest bardzo praktyczne.
Przykład praktyczny: Ile wynosi pole trójkąta równobocznego o boku 10 cm?
Zobaczmy, jak zastosować ten wzór w praktyce:
- Dane: Trójkąt równoboczny o długości boku 'a' = 10 cm.
- Wzór: P = (a²√3) / 4
- Podstawienie wartości: P = (10²√3) / 4
- Obliczenia: P = (100√3) / 4
- Uproszczenie: P = 25√3 cm².
Wynik często pozostawia się w takiej formie z pierwiastkiem, chyba że zadanie wymaga przybliżenia dziesiętnego. Wtedy √3 to około 1,732.
Brak wysokości? Trzy sprawdzone metody na pole trójkąta
Co zrobić, gdy zadanie nie podaje wysokości trójkąta, a Ty nie masz do czynienia z trójkątem prostokątnym ani równobocznym? Bez obaw! Matematyka ma na to rozwiązania. Istnieją inne, bardziej zaawansowane metody, które pozwalają obliczyć pole trójkąta, bazując na innych danych. To pokazuje, jak elastyczna potrafi być geometria.
Metoda 1: Wzór Herona, czyli jak obliczyć pole trójkąta znając 3 boki
Wzór Herona to prawdziwy ratunek, gdy znasz długości wszystkich trzech boków trójkąta (a, b, c), ale nie masz pojęcia o jego wysokości. Jest to nieco bardziej złożony wzór, ale niezwykle skuteczny. Najpierw musimy obliczyć połowę obwodu trójkąta, którą oznaczamy jako 'p'.
Wzór na 'p': p = (a + b + c) / 2 Wzór Herona na pole: P = √[p(p-a)(p-b)(p-c)]
Przykład:
- Dane: Trójkąt o bokach a = 3 cm, b = 4 cm, c = 5 cm.
- Obliczamy 'p': p = (3 + 4 + 5) / 2 = 12 / 2 = 6 cm.
- Podstawiamy do wzoru Herona: P = √[6(6-3)(6-4)(6-5)]
- Obliczenia: P = √[6 * 3 * 2 * 1] = √36
- Wynik: P = 6 cm².
To bardzo przydatny wzór, który warto znać, zwłaszcza w liceum.
Metoda 2: Trygonometria na ratunek - wykorzystaj sinus kąta między bokami
Jeśli znasz długości dwóch boków trójkąta oraz miarę kąta zawartego między nimi, możesz skorzystać ze wzoru trygonometrycznego. Jest to eleganckie rozwiązanie, które wykorzystuje funkcję sinus. Wzór wygląda następująco: P = 1/2 * a * b * sin(γ), gdzie 'a' i 'b' to długości znanych boków, a 'γ' (gamma) to kąt między nimi.
Przykład:
Mamy trójkąt, w którym bok 'a' = 7 cm, bok 'b' = 10 cm, a kąt między nimi wynosi 30 stopni. (Wartość sin(30°) = 0,5). P = 1/2 * 7 cm * 10 cm * sin(30°) P = 1/2 * 70 cm² * 0,5 P = 35 cm² * 0,5 P = 17,5 cm².
Ten wzór jest szczególnie użyteczny, gdy pracujemy z kątami i funkcjami trygonometrycznymi.
Metoda 3: Pole z współrzędnych wierzchołków (sposób dla zaawansowanych)
Dla tych, którzy zgłębiają geometrię analityczną, istnieje metoda obliczania pola trójkąta, gdy znane są współrzędne jego wierzchołków. Jeśli wierzchołki trójkąta to A=(x₁, y₁), B=(x₂, y₂), C=(x₃, y₃), pole można obliczyć ze wzoru: P = 1/2 |(x₂ - x₁)(y₃ - y₁) - (y₂ - y₁)(x₃ - x₁)|. Pionowe kreski oznaczają wartość bezwzględną, ponieważ pole zawsze musi być dodatnie. Jest to metoda, którą zazwyczaj poznaje się w liceum i wymaga precyzyjnych obliczeń.
Od teorii do praktyki: rozwiąż przykładowe zadania
Teraz, gdy znasz już różne wzory, czas na praktykę! Wierzę, że najlepszym sposobem na utrwalenie wiedzy jest samodzielne rozwiązywanie zadań. Przygotowałem dla Ciebie kilka typowych problemów, które pomogą Ci sprawdzić swoje umiejętności i upewnić się, że rozumiesz, kiedy zastosować który wzór.
Zadanie 1: Klasyczny problem z podstawą i wysokością
Oblicz pole trójkąta, którego podstawa ma długość 12 cm, a wysokość opuszczona na tę podstawę wynosi 7 cm.
- Zidentyfikuj dane: Podstawa a = 12 cm, wysokość h = 7 cm.
- Wybierz wzór: P = (a * h) / 2.
- Podstaw wartości: P = (12 cm * 7 cm) / 2.
- Wykonaj obliczenia: P = 84 cm² / 2.
- Podaj wynik: P = 42 cm².
Zadanie 2: Obliczanie pola trójkąta, gdy znasz tylko długości jego boków
Trójkąt ma boki o długościach 5 cm, 6 cm i 7 cm. Oblicz jego pole.
- Zidentyfikuj dane: a = 5 cm, b = 6 cm, c = 7 cm.
- Wybierz wzór: Wzór Herona, ponieważ znamy wszystkie trzy boki. Najpierw oblicz 'p' (połowę obwodu).
- Oblicz 'p': p = (5 + 6 + 7) / 2 = 18 / 2 = 9 cm.
- Podstaw do wzoru Herona: P = √[p(p-a)(p-b)(p-c)] = √[9(9-5)(9-6)(9-7)].
- Wykonaj obliczenia: P = √[9 * 4 * 3 * 2] = √216.
- Uprość pierwiastek (jeśli to możliwe): √216 = √(36 * 6) = 6√6 cm².
- Podaj wynik: P = 6√6 cm².
Zadanie 3: Wykorzystanie funkcji trygonometrycznych w praktyce
Oblicz pole trójkąta, w którym dwa boki mają długości 8 cm i 12 cm, a kąt między nimi wynosi 60 stopni.
- Zidentyfikuj dane: a = 8 cm, b = 12 cm, γ = 60°. (Pamiętaj, że sin(60°) = √3/2).
- Wybierz wzór: Wzór trygonometryczny P = 1/2 * a * b * sin(γ).
- Podstaw wartości: P = 1/2 * 8 cm * 12 cm * sin(60°).
- Wykonaj obliczenia: P = 1/2 * 96 cm² * (√3/2).
- Uprość: P = 48 cm² * (√3/2) = 24√3 cm².
- Podaj wynik: P = 24√3 cm².
Unikaj błędów: najczęstsze pomyłki przy obliczaniu pola trójkąta
Nawet najbardziej doświadczonym zdarzają się pomyłki, a w matematyce łatwo o drobne potknięcia, które prowadzą do błędnego wyniku. Z mojego doświadczenia wiem, że pewne błędy powtarzają się częściej niż inne. Chcę Cię przed nimi przestrzec, abyś mógł ich unikać i cieszyć się poprawnymi rozwiązaniami.
Błędny wybór wzoru do typu trójkąta
To chyba najczęstszy błąd. Uczniowie często próbują stosować podstawowy wzór P = (a * h) / 2, nawet gdy nie mają podanej wysokości, zamiast sięgnąć po wzór Herona czy trygonometryczny. Innym przykładem jest używanie wzoru na trójkąt równoboczny dla trójkąta, który nim nie jest. Zawsze najpierw dokładnie zidentyfikuj typ trójkąta i dostępne dane, a dopiero potem wybierz odpowiedni wzór. To podstawa sukcesu!
Nieprawidłowe podstawienie danych do wzoru
Kolejny błąd to mylenie danych. Na przykład, w trójkącie prostokątnym zdarza się podstawiać długość przeciwprostokątnej jako jedną z przyprostokątnych do wzoru P = (a * b) / 2. Albo w podstawowym wzorze P = (a * h) / 2, pomylenie podstawy z wysokością. Dokładnie czytaj treść zadania i upewnij się, że każda wartość trafia w odpowiednie miejsce we wzorze.
Pomyłki w kolejności wykonywania działań
Matematyka ma swoje zasady, a jedną z najważniejszych jest kolejność wykonywania działań. W obliczeniach pola trójkąta, zwłaszcza tych z pierwiastkami (jak we wzorze Herona czy dla trójkąta równobocznego) lub ułamkami, łatwo o błąd, jeśli zapomnimy o tej kolejności. Pamiętaj: najpierw nawiasy, potem potęgowanie i pierwiastkowanie, następnie mnożenie i dzielenie, na końcu dodawanie i odejmowanie. Precyzja to klucz!Szybsze sposoby: odkryj moc kalkulatorów online
W dzisiejszych czasach technologia przychodzi nam z pomocą w wielu dziedzinach, a matematyka nie jest wyjątkiem. Kalkulatory online do obliczania pola trójkąta to narzędzia, które mogą być bardzo przydatne w określonych sytuacjach. Warto wiedzieć, jak działają i kiedy warto z nich skorzystać.
Jak działają internetowe kalkulatory pola trójkąta?
Internetowe kalkulatory pola trójkąta są niezwykle proste w obsłudze. Zazwyczaj wystarczy wybrać typ danych, które posiadasz (np. podstawa i wysokość, trzy boki, dwa boki i kąt) i wprowadzić odpowiednie wartości w wyznaczone pola. Po kliknięciu przycisku "oblicz" lub podobnego, kalkulator natychmiast wyświetli wynik. To szybkie, wygodne i minimalizuje ryzyko błędów rachunkowych.
Przeczytaj również: Nauczanie indywidualne w szkole? Tak! Jak je zorganizować?
Kiedy warto z nich skorzystać, a kiedy lepiej liczyć samodzielnie?
Kalkulatory online są świetne do szybkiego sprawdzenia swoich wyników z zadania domowego lub do uzyskania natychmiastowej odpowiedzi, gdy potrzebujesz jej do jakiegoś praktycznego zastosowania (np. obliczenia powierzchni materiału). Mogą też pomóc w zrozumieniu, jak różne dane wpływają na pole. Jednakże, nie zastąpią one samodzielnej nauki i zrozumienia procesu. Na egzaminach czy testach nie będziesz miał do nich dostępu, dlatego kluczowe jest, abyś potrafił liczyć pole trójkąta samodzielnie, krok po kroku. Używaj kalkulatorów jako narzędzia pomocniczego, a nie zamiennika dla własnej wiedzy.