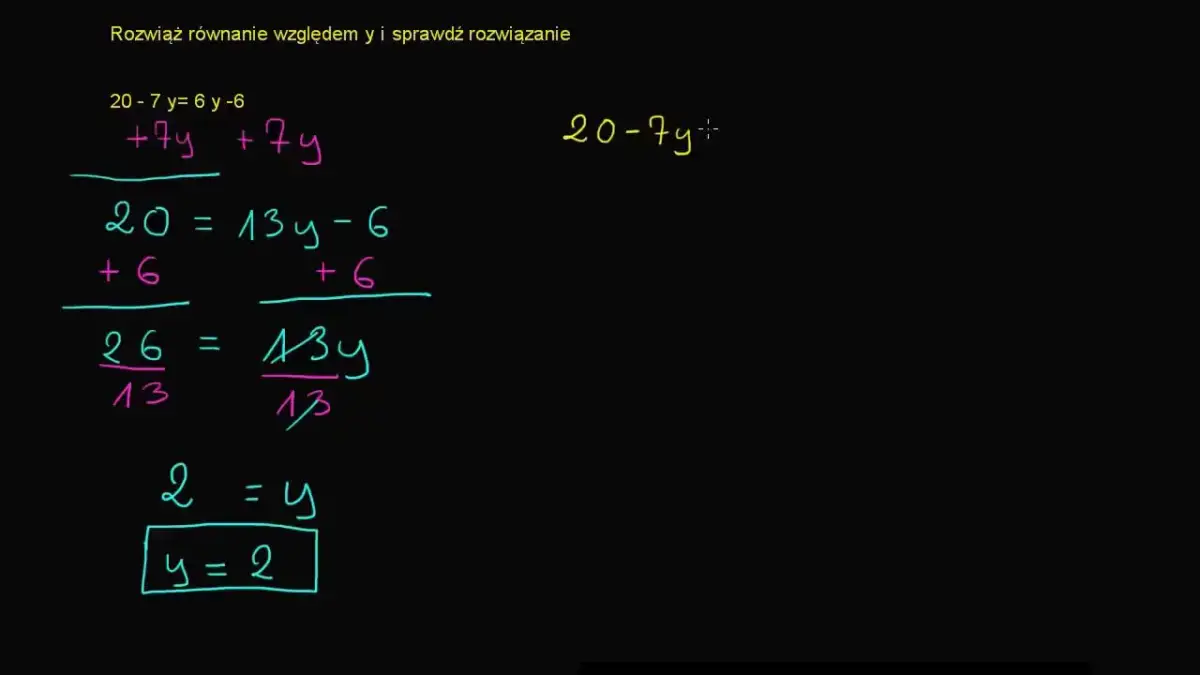Rozwiązywanie równań praktyczny przewodnik krok po kroku dla każdego
- Rozwiązywanie równania polega na znalezieniu liczb (pierwiastków), które po podstawieniu w miejsce niewiadomej czynią równanie prawdziwym.
- Podstawowe zasady przekształcania równań obejmują dodawanie/odejmowanie tego samego wyrażenia po obu stronach oraz mnożenie/dzielenie przez tę samą liczbę różną od zera.
- Równania liniowe rozwiązuje się przez przenoszenie wyrazów z niewiadomą na jedną stronę, a wolnych na drugą, redukcję i dzielenie.
- Równania kwadratowe najczęściej rozwiązuje się za pomocą delty (Δ = b² - 4ac) lub faktoryzacji.
- Równania mogą być oznaczone (jedno rozwiązanie), tożsamościowe (nieskończenie wiele rozwiązań) lub sprzeczne (brak rozwiązań).
- Częste błędy to błędna zmiana znaków, dzielenie przez zero lub pomyłki w kolejności działań.
Kluczowe pojęcia, które musisz znać: niewiadoma, współczynnik i rozwiązanie
Zanim zagłębimy się w techniki rozwiązywania, musimy zrozumieć, czym w ogóle jest równanie. W najprostszych słowach, równanie to stwierdzenie, że dwa wyrażenia matematyczne są sobie równe. Zawsze zawiera znak równości (=) i przynajmniej jedną niewiadomą. Rozwiązanie równania polega na znalezieniu wszystkich liczb (nazywanych pierwiastkami), które po podstawieniu w miejsce niewiadomej sprawiają, że równanie staje się prawdziwą równością.
- Niewiadoma: Symbol (najczęściej litera, np. x, y, z), który reprezentuje nieznaną wartość, którą chcemy znaleźć. Jest to "zagadka" do rozwiązania.
- Współczynnik: Liczba, która mnoży niewiadomą w równaniu (np. w 3x, 3 jest współczynnikiem). Wyrazy wolne to liczby, które nie są mnożone przez niewiadomą.
- Rozwiązanie (pierwiastek): Wartość lub zbiór wartości niewiadomej, które po podstawieniu do równania sprawiają, że lewa strona równa się prawej. To jest nasz "wynik".
Złote zasady przekształcania równań, których nie możesz złamać
Aby rozwiązać równanie, musimy je przekształcać w taki sposób, aby nie zmienić jego rozwiązania. Istnieją dwie podstawowe zasady, które są fundamentem każdej operacji na równaniach. Moim zdaniem, ich zrozumienie to klucz do sukcesu.
- Dodawanie lub odejmowanie tego samego wyrażenia po obu stronach równania: Możemy dodać lub odjąć dowolną liczbę lub wyrażenie od obu stron równania, a jego rozwiązanie pozostanie bez zmian. To jak waga jeśli dodasz lub odejmiesz ten sam ciężar z obu szalek, waga nadal będzie w równowadze. Na przykład, jeśli masz równanie x - 5 = 10, możesz dodać 5 do obu stron, aby otrzymać x = 15.
- Mnożenie lub dzielenie obu stron równania przez tę samą liczbę różną od zera: Możemy pomnożyć lub podzielić obie strony równania przez dowolną liczbę, byleby była ona różna od zera. Dzielenie przez zero jest operacją niedozwoloną w matematyce i prowadziłoby do błędnych wyników. Jeśli masz równanie 2x = 10, możesz podzielić obie strony przez 2, aby otrzymać x = 5.

Równania liniowe krok po kroku: opanuj absolutne podstawy
Równania liniowe, zwane też równaniami pierwszego stopnia z jedną niewiadomą, są najprostszym typem równań. Ich ogólna postać to ax + b = 0, gdzie 'a' i 'b' to znane liczby (współczynniki), a 'x' to niewiadoma. Rozwiązywanie ich to podstawa, którą musisz opanować.
Schemat postępowania: Jak przenieść niewiadome na jedną stronę?
Oto sprawdzony schemat, który zawsze działa przy równaniach liniowych:
- Przeniesienie wyrazów z niewiadomą na jedną stronę, a wyrazów wolnych na drugą: Zazwyczaj dążymy do tego, aby wszystkie wyrazy zawierające 'x' znalazły się po lewej stronie równania, a wszystkie liczby (wyrazy wolne) po prawej.
- Zmiana znaku przy przenoszeniu: Pamiętaj, że kiedy przenosisz wyraz z jednej strony równania na drugą, musisz zmienić jego znak na przeciwny. Jeśli wyraz był dodatni, staje się ujemny i odwrotnie. To bardzo częste źródło błędów, więc bądź czujny!
- Redukcja wyrazów podobnych: Po przeniesieniu wyrazów, uprość obie strony równania, sumując lub odejmując wyrazy podobne (np. 3x + 2x = 5x, a 7 - 4 = 3).
- Dzielenie przez współczynnik przy niewiadomej: Ostatnim krokiem jest podzielenie obu stron równania przez liczbę stojącą przy niewiadomej 'x'. Dzięki temu po jednej stronie zostanie samo 'x', a po drugiej jego wartość.
Praktyczne przykłady: Rozwiązujemy proste równania od A do Z
Zobaczmy, jak to działa w praktyce. Te przykłady pomogą Ci utrwalić schemat.
Przykład 1: 3x + 7 = 19
1. Przenosimy wyraz wolny (+7) na prawą stronę, zmieniając znak:
3x = 19 - 7
2. Redukujemy wyrazy podobne:
3x = 12
3. Dzielimy obie strony przez współczynnik przy x (czyli przez 3):
x = 12 / 3
x = 4
Przykład 2: 5x - 4 = 2x + 11
1. Przenosimy wyrazy z niewiadomą (2x) na lewą stronę, a wyraz wolny (-4) na prawą, pamiętając o zmianie znaków:
5x - 2x = 11 + 4
2. Redukujemy wyrazy podobne po obu stronach:
3x = 15
3. Dzielimy obie strony przez 3:
x = 15 / 3
x = 5
Co zrobić, gdy pojawiają się nawiasy i ułamki? Sprawdzone techniki
Czasem równania liniowe wyglądają nieco bardziej skomplikowanie, bo zawierają nawiasy lub ułamki. Nie martw się, to tylko dodatkowe kroki na początku!
-
Nawiasy: Jeśli w równaniu występują nawiasy, najpierw musisz je opuścić, mnożąc liczbę stojącą przed nawiasem przez każdy wyraz w nawiasie.
Przykład: 2(x + 3) = 10
2x + 6 = 10 (wymnożyliśmy 2 przez x i przez 3)
Dalej postępujemy standardowo: 2x = 10 - 6 -> 2x = 4 -> x = 2. -
Ułamki: Gdy masz do czynienia z ułamkami, najłatwiejszym sposobem jest pomnożenie obu stron równania przez wspólny mianownik wszystkich ułamków. To pozwoli "pozbyć się" mianowników.
Przykład: x/2 + 1/3 = 5/6
Wspólny mianownik dla 2, 3 i 6 to 6. Mnożymy całe równanie przez 6:
6 * (x/2) + 6 * (1/3) = 6 * (5/6)
3x + 2 = 5
Dalej standardowo: 3x = 5 - 2 -> 3x = 3 -> x = 1.
Gdy pojawia się potęga: Jak poradzić sobie z równaniem kwadratowym?
Po opanowaniu równań liniowych, kolejnym krokiem są równania kwadratowe. Są one nieco bardziej złożone, ponieważ zawierają niewiadomą podniesioną do potęgi drugiej (x²). Ich ogólna postać to ax² + bx + c = 0, gdzie 'a', 'b', 'c' to znane liczby, a 'a' musi być różne od zera (bo inaczej byłoby to równanie liniowe).
Metoda uniwersalna: Czym jest słynna delta (Δ) i jak ją obliczyć?
Najbardziej uniwersalną i niezawodną metodą rozwiązywania równań kwadratowych jest użycie wyróżnika trójmianu kwadratowego, czyli słynnej delty (Δ). Delta jest obliczana ze wzoru:
Δ = b² - 4ac
Wartość delty jest kluczowa, ponieważ informuje nas o liczbie rozwiązań równania kwadratowego:
- Jeśli Δ > 0 (delta jest dodatnia): Równanie ma dwa różne rozwiązania rzeczywiste (dwa pierwiastki).
- Jeśli Δ = 0 (delta jest równa zero): Równanie ma dokładnie jedno rozwiązanie rzeczywiste (jeden pierwiastek podwójny).
- Jeśli Δ < 0 (delta jest ujemna): Równanie nie ma rozwiązań rzeczywistych. W tym przypadku rozwiązania istnieją w zbiorze liczb zespolonych, ale na poziomie szkoły średniej zazwyczaj uznajemy, że brak jest rozwiązań.
Krok po kroku: Obliczanie pierwiastków za pomocą delty na przykładach
Po obliczeniu delty, jeśli jest ona większa lub równa zero, możemy znaleźć rozwiązania (pierwiastki) równania kwadratowego za pomocą następujących wzorów:
x₁ = (-b - √Δ) / 2a
x₂ = (-b + √Δ) / 2a
Przejdźmy do przykładów, aby to lepiej zrozumieć.
Przykład 1 (Δ > 0): x² - 5x + 6 = 0
Tutaj mamy a = 1, b = -5, c = 6.
1. Obliczamy deltę:
Δ = (-5)² - 4 * 1 * 6 = 25 - 24 = 1
Ponieważ Δ = 1 > 0, równanie ma dwa rozwiązania.
2. Obliczamy pierwiastki:
√Δ = √1 = 1
x₁ = ( -(-5) - 1 ) / (2 * 1) = (5 - 1) / 2 = 4 / 2 = 2
x₂ = ( -(-5) + 1 ) / (2 * 1) = (5 + 1) / 2 = 6 / 2 = 3
x² - 4x + 4 = 0
Tutaj mamy a = 1, b = -4, c = 4.
1. Obliczamy deltę:
Δ = (-4)² - 4 * 1 * 4 = 16 - 16 = 0
Ponieważ Δ = 0, równanie ma jedno rozwiązanie (pierwiastek podwójny).
2. Obliczamy pierwiastek:
x = (-b) / (2a) = (-(-4)) / (2 * 1) = 4 / 2 = 2
Przykład 3 (Δ < 0): x² + 2x + 5 = 0
Tutaj mamy a = 1, b = 2, c = 5.
1. Obliczamy deltę:
Δ = 2² - 4 * 1 * 5 = 4 - 20 = -16
Ponieważ Δ = -16 < 0, równanie nie ma rozwiązań rzeczywistych.
Szybsza droga dla sprytnych: Kiedy warto zastosować faktoryzację (rozkład na czynniki)?
Faktoryzacja, czyli rozkład na czynniki, to alternatywna metoda rozwiązywania równań kwadratowych, która bywa szybsza, jeśli trójmian kwadratowy jest łatwy do rozłożenia. Polega na przedstawieniu równania w postaci iloczynu dwóch nawiasów, np. (x - x₁)(x - x₂) = 0. Rozwiązania odczytujemy wtedy bezpośrednio jako x = x₁ lub x = x₂.
Ta metoda jest szczególnie przydatna w przypadku równań niezupełnych (gdy b=0 lub c=0) lub gdy widzimy, że trójmian jest wzorem skróconego mnożenia. Na przykład, równanie x² - 9 = 0 można zapisać jako (x - 3)(x + 3) = 0. Stąd od razu widać, że rozwiązania to x = 3 lub x = -3. Podobnie, równanie x² - 5x = 0 można zapisać jako x(x - 5) = 0, co daje rozwiązania x = 0 lub x = 5. Warto ćwiczyć rozpoznawanie takich sytuacji, aby zaoszczędzić czas.
Nie każde równanie ma rozwiązanie! Jak rozpoznać typy odpowiedzi?
Wbrew pozorom, nie każde równanie, które napotkasz, będzie miało jedno, konkretne rozwiązanie. W matematyce wyróżniamy trzy główne typy równań ze względu na liczbę rozwiązań. Zrozumienie ich pomoże Ci uniknąć frustracji, gdy wynik nie będzie "oczekiwany".
Równanie oznaczone: Gdy istnieje jedna, konkretna odpowiedź
Równanie oznaczone to takie, które posiada dokładnie jedno rozwiązanie. Jest to najczęściej spotykany typ równań, zwłaszcza na początkowych etapach nauki. Większość przykładów, które rozwiązywaliśmy do tej pory, to równania oznaczone.
Przykład: 2x + 5 = 11
2x = 11 - 5
2x = 6
x = 6 / 2
x = 3
Istnieje tylko jedna liczba (3), która spełnia to równanie, więc jest ono oznaczone.
Równanie tożsamościowe: Kiedy każda liczba jest poprawnym wynikiem?
Równanie tożsamościowe to równanie, które posiada nieskończenie wiele rozwiązań. Oznacza to, że każda liczba rzeczywista podstawiona w miejsce niewiadomej sprawi, że równanie będzie prawdziwe. Zazwyczaj dzieje się tak, gdy po przekształceniach obie strony równania stają się identyczne.
Przykład: 3(x + 1) = 3x + 3
Opuszczamy nawiasy:
3x + 3 = 3x + 3
Przenosimy wyrazy z x na lewą stronę, a liczby na prawą:
3x - 3x = 3 - 3
0 = 0
Otrzymaliśmy prawdziwą równość (0=0), która nie zawiera niewiadomej. To oznacza, że równanie jest tożsamościowe, a jego rozwiązaniem jest każda liczba rzeczywista.
Równanie sprzeczne: Jak rozpoznać sytuację bez wyjścia (brak rozwiązań)?
Równanie sprzeczne to takie, które nie posiada żadnego rozwiązania. Niezależnie od tego, jaką liczbę podstawimy w miejsce niewiadomej, równanie nigdy nie będzie prawdziwe. W trakcie rozwiązywania równania sprzecznego, po przekształceniach otrzymamy fałszywą równość.
Przykład: x + 7 = x + 10
Przenosimy wyrazy z x na lewą stronę, a liczby na prawą:
x - x = 10 - 7
0 = 3
Otrzymaliśmy fałszywą równość (0=3). To oznacza, że równanie jest sprzeczne i nie ma rozwiązania.
Uniknij frustracji: Najczęstsze pułapki i błędy przy rozwiązywaniu równań
Jako Alan Szymczak, widziałem niezliczoną ilość prac domowych i egzaminów, gdzie te same błędy powtarzały się raz po raz. Zrozumienie najczęstszych pułapek jest równie ważne, jak znajomość samych metod. Pozwoli Ci to świadomie unikać pomyłek i oszczędzić sobie frustracji.
Błąd nr 1: Gubienie minusów, czyli pułapka ze zmianą znaków
To chyba najpopularniejszy błąd! Podczas przenoszenia wyrazów z jednej strony równania na drugą, koniecznie trzeba zmienić ich znak na przeciwny. Zapomnienie o tym prowadzi do błędnych wyników.
Przykład błędny: 3x - 5 = 10
Błędne przeniesienie: 3x = 10 - 5 (znak -5 nie został zmieniony)
3x = 5
x = 5/3
Prawidłowe postępowanie: 3x - 5 = 10
Prawidłowe przeniesienie: 3x = 10 + 5 (znak -5 został zmieniony na +5)
3x = 15
x = 15/3
x = 5
Błąd nr 2: Niebezpieczne dzielenie przez zero jak nie stracić rozwiązania?
Pamiętaj, że nigdy nie wolno dzielić przez zero. Ale pułapka jest bardziej subtelna: nie wolno dzielić obu stron równania przez wyrażenie zawierające niewiadomą (np. 'x'), jeśli nie jesteś pewien, że to wyrażenie jest różne od zera. Dzielenie przez 'x' zakłada, że x ≠ 0, co może prowadzić do utraty rozwiązania x = 0, jeśli takie istnieje.
Przykład błędny: x² = 5x
Błędne dzielenie przez x: x = 5 (straciliśmy rozwiązanie x=0)
Prawidłowe postępowanie: x² = 5x
Przenosimy wszystko na jedną stronę: x² - 5x = 0
Wyłączamy x przed nawias: x(x - 5) = 0
Z tego wynika, że x = 0 lub x - 5 = 0, czyli x = 0 lub x = 5.
W ten sposób znajdujemy oba rozwiązania.
Błąd nr 3: Pomyłki w kolejności działań i opuszczaniu nawiasów
Matematyka ma swoje zasady dotyczące kolejności działań (najpierw nawiasy, potem potęgi, mnożenie/dzielenie, na końcu dodawanie/odejmowanie). Nieprzestrzeganie ich to prosta droga do błędu. Podobnie, opuszczając nawiasy, upewnij się, że mnożysz liczbę stojącą przed nawiasem przez KAŻDY wyraz w nawiasie.
Przykład błędny: 2(x + 3) = 2x + 3 (zapomniano pomnożyć 2 przez 3)
Prawidłowo: 2(x + 3) = 2x + 6
Przykład błędny: -(x - 4) = -x - 4 (zapomniano zmienić znak -4 na +4)
Prawidłowo: -(x - 4) = -x + 4
Dlaczego sprawdzanie wyniku to Twój najlepszy przyjaciel?
Poświęć dodatkową minutę na sprawdzenie swojego rozwiązania. To proste: podstaw otrzymany wynik z powrotem do oryginalnego równania. Jeśli lewa strona równa się prawej, to masz pewność, że Twoje rozwiązanie jest poprawne. Jeśli nie, wiesz, że gdzieś popełniłeś błąd i możesz go znaleźć. To moim zdaniem jeden z najważniejszych nawyków, który powinieneś sobie wyrobić.
Matematyka w erze cyfrowej: Czy technologia może pomóc w nauce?
Żyjemy w czasach, gdy technologia jest na wyciągnięcie ręki. W nauce matematyki również możemy z niej korzystać, ale z głową. Nowoczesne narzędzia to świetne wsparcie, ale nigdy nie powinny zastępować samodzielnego myślenia i zrozumienia.
Aplikacje i kalkulatory online jako wsparcie, a nie zastępstwo
Istnieje wiele aplikacji mobilnych i kalkulatorów online, które potrafią rozwiązywać równania, a nawet pokazywać kroki rozwiązania. Narzędzia takie jak Wolfram Alpha, GeoGebra czy Desmos mogą być nieocenione, gdy:
- Chcesz szybko zweryfikować swój wynik po samodzielnym rozwiązaniu.
- Potrzebujesz zobaczyć, jak wygląda rozwiązanie równania, którego nie potrafisz ruszyć, aby zrozumieć poszczególne kroki.
- Chcesz zbadać, jak zmiana współczynników wpływa na rozwiązanie równania.
Pamiętaj jednak, że ich głównym celem jest wsparcie w nauce i weryfikacji, a nie wyręczanie Cię z myślenia. Używaj ich mądrze, aby pogłębić swoje zrozumienie, a nie tylko uzyskać gotową odpowiedź.
Przeczytaj również: Jak obliczyć pole trójkąta? Wszystkie wzory i przykłady krok po kroku
Wizualizacja ma znaczenie: Jak wykresy pomagają zrozumieć rozwiązania?
Dla wielu osób matematyka staje się łatwiejsza, gdy mogą ją "zobaczyć". Narzędzia do wizualizacji graficznej, takie jak wspomniane GeoGebra czy Desmos, pozwalają przedstawić równania w formie wykresów. To niezwykle pomocne, zwłaszcza przy równaniach liniowych i kwadratowych:
- Równania liniowe: Każda strona równania liniowego może być potraktowana jako funkcja liniowa (y = ax + b). Rozwiązanie równania to punkt przecięcia się wykresów tych dwóch funkcji. Na przykład, dla 2x + 5 = 11, rysujemy y = 2x + 5 i y = 11. Ich punkt przecięcia pokaże nam wartość x, która jest rozwiązaniem.
- Równania kwadratowe: Równanie kwadratowe ax² + bx + c = 0 to nic innego jak szukanie miejsc zerowych funkcji kwadratowej f(x) = ax² + bx + c. Wykres tej funkcji to parabola. Rozwiązania równania to punkty, w których parabola przecina oś X. Jeśli parabola nie przecina osi X, oznacza to brak rozwiązań rzeczywistych (Δ < 0).
Wizualizacja pomaga zbudować intuicję i lepiej zrozumieć, co tak naprawdę oznacza "rozwiązanie równania". Zachęcam Cię do eksperymentowania z tymi narzędziami to naprawdę może zmienić Twoje podejście do matematyki!