Jak rozwiązać równanie z ułamkiem? Opanuj to krok po kroku!

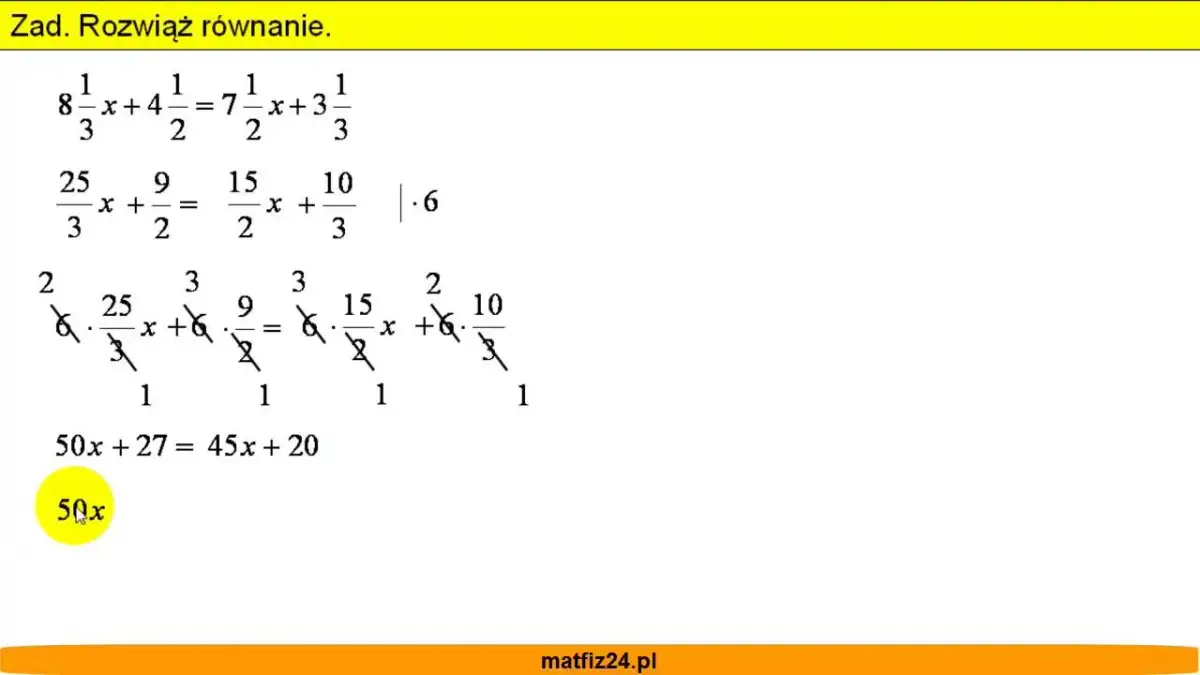
Rozwiązywanie równań z ułamkami bywa dla wielu uczniów wyzwaniem, ale zapewniam, że z odpowiednim podejściem i zrozumieniem kluczowych zasad, staje się znacznie prostsze. Ten artykuł to praktyczny przewodnik krok po kroku, który ma na celu rozwiać wszelkie wątpliwości i wyposażyć Cię w narzędzia niezbędne do skutecznego radzenia sobie z tego typu zadaniami, niezależnie od ich złożoności.

Równania z ułamkami często postrzegane są jako trudne, ponieważ wymagają dwuetapowego podejścia. Najpierw musimy pozbyć się ułamków, a dopiero potem możemy rozwiązać uproszczone równanie liniowe. To właśnie ten pierwszy krok, czyli eliminacja ułamków, bywa dla wielu problematyczny. Moim celem jest uproszczenie tego procesu i pokazanie, że każdy może go opanować.

Podstawowa zasada eliminowania ułamków z równań jest niezwykle prosta: chodzi o to, aby przekształcić równanie ułamkowe w równanie liniowe, z którym znacznie łatwiej sobie poradzić. Ułamki są często źródłem pomyłek, więc ich usunięcie to pierwszy i najważniejszy krok do sukcesu.

„Złota zasada” rozwiązywania równań z ułamkami polega na pomnożeniu obu stron równania przez mianownik (lub wspólny mianownik, jeśli ułamków jest więcej). To działanie jest absolutnie kluczowe, ponieważ pozwala nam zachować równość równania, jednocześnie eliminując ułamki. Dzięki temu równanie staje się „czystsze” i łatwiejsze do rozwiązania.

Rozwiązywanie równań z jednym ułamkiem zwykłym

Zacznijmy od najprostszego przypadku: równania z pojedynczym ułamkiem zwykłym. To doskonały punkt wyjścia do zrozumienia podstawowej metody.

1. Przykład równania: `x/3 = 5`
2. Cel: Chcemy pozbyć się mianownika (3).
3. Działanie: Mnożymy obie strony równania przez mianownik, czyli przez 3.
   • `(x/3) * 3 = 5 * 3`
4. Uproszczenie: Po pomnożeniu trójki po lewej stronie się skracają.
   • `x = 15`
5. Rozwiązanie: Otrzymujemy `x = 15`.

Bardzo ważna uwaga: jeśli licznik ułamka jest sumą lub różnicą, zawsze musimy użyć nawiasów, mnożąc przez mianownik. Pominięcie nawiasów to jeden z najczęstszych błędów, który prowadzi do błędnych wyników. Na przykład, jeśli mamy `(x+1)/2 = 3`, prawidłowe działanie to `(x+1) = 3 * 2`, co daje `x+1 = 6` i w konsekwencji `x = 5`. Błędem byłoby napisanie `x+1*2 = 3`.

Równania z wieloma ułamkami zwykłymi

Kiedy w równaniu pojawia się kilka ułamków o różnych mianownikach, metoda jest podobna, ale wymaga jednego dodatkowego kroku: znalezienia wspólnego mianownika.

Pojęcie najmniejszego wspólnego mianownika (NWW) jest tu kluczowe. NWW to najmniejsza liczba, która jest wielokrotnością wszystkich mianowników w równaniu. Aby ją znaleźć, często wystarczy wypisać wielokrotności każdego mianownika i znaleźć najmniejszą wspólną. Na przykład, dla mianowników 2, 3 i 4, NWW to 12 (bo 12 jest podzielne przez 2, 3 i 4).

1. Przykład równania: `x/2 + x/3 = 5`
2. Znalezienie NWW: Mianowniki to 2 i 3. Najmniejsza wspólna wielokrotność dla 2 i 3 to 6.
3. Działanie: Mnożymy każdy wyraz po obu stronach równania przez NWW, czyli przez 6.
   • `(x/2) * 6 + (x/3) * 6 = 5 * 6`
4. Uproszczenie: Wykonujemy mnożenie i skracanie.
   • `3x + 2x = 30`
5. Rozwiązanie: Upraszczamy równanie liniowe.
   • `5x = 30`
   • `x = 30 / 5`
   • `x = 6`

Równania z ułamkami dziesiętnymi

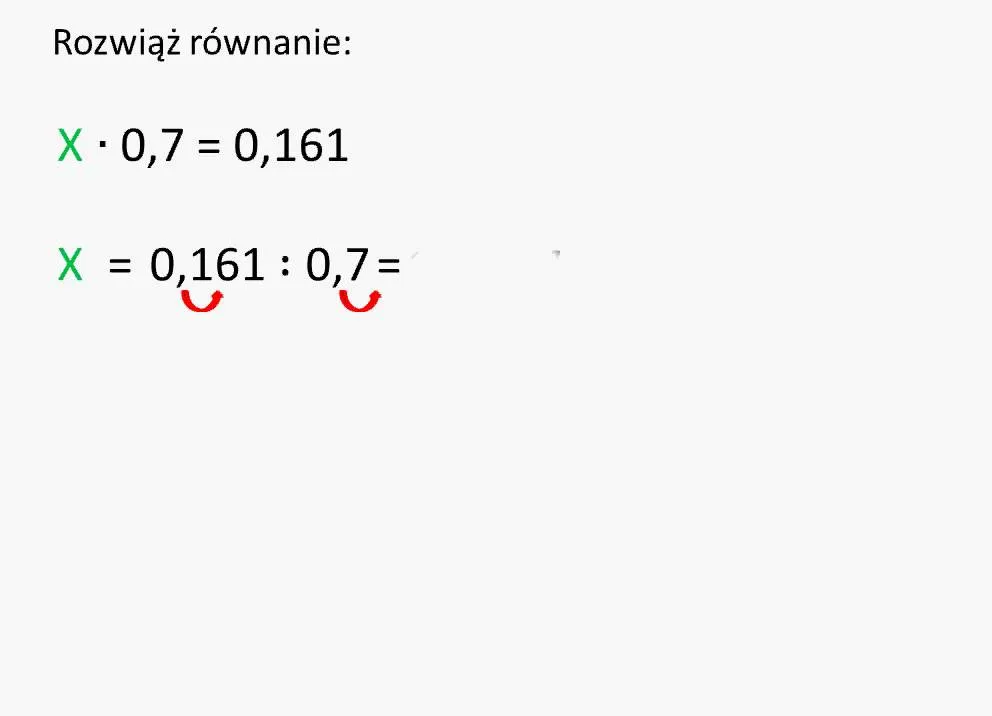
Równania z ułamkami dziesiętnymi często można rozwiązywać bezpośrednio, zwłaszcza jeśli są proste (np. 0.5x). Jednak istnieje również skuteczna metoda eliminowania przecinków, która może uprościć obliczenia, szczególnie przy bardziej złożonych liczbach.

1. Przykład równania: `0.2x + 0.5 = 1.3`
2. Cel: Chcemy pozbyć się przecinków. Największa liczba miejsc po przecinku to jedno (0.2, 0.5, 1.3).
3. Działanie: Mnożymy obie strony równania przez odpowiednią potęgę liczby 10. W tym przypadku wystarczy pomnożyć przez 10 (bo mamy jedno miejsce po przecinku).
   • `(0.2x) * 10 + (0.5) * 10 = (1.3) * 10`
4. Uproszczenie: Wykonujemy mnożenie.
   • `2x + 5 = 13`
5. Rozwiązanie: Rozwiązujemy powstałe równanie liniowe.
   • `2x = 13 - 5`
   • `2x = 8`
   • `x = 8 / 2`
   • `x = 4`

Równania z niewiadomą w mianowniku (równania wymierne)

Równania z niewiadomą (x) w mianowniku to bardziej zaawansowany przypadek, który wymaga szczególnej uwagi. Kluczowe jest rozpoczęcie od wyznaczenia dziedziny równania. Oznacza to, że musimy określić wszystkie wartości 'x', dla których mianownik nie może być równy zero, ponieważ dzielenie przez zero jest matematycznie niedopuszczalne. Pamiętaj, pominięcie tego kroku może prowadzić do zaakceptowania błędnych rozwiązań, które w rzeczywistości nie istnieją.

1. Przykład równania: `1/(x-2) = 3`
2. Wyznaczenie dziedziny: Mianownik to `(x-2)`. Musimy założyć, że `x-2 ≠ 0`, czyli `x ≠ 2`. Zatem dziedziną są wszystkie liczby rzeczywiste z wyjątkiem 2.
3. Działanie: Mnożymy obie strony równania przez mianownik, czyli przez `(x-2)`. Pamiętaj o nawiasach!
   • `(1/(x-2)) * (x-2) = 3 * (x-2)`
4. Uproszczenie: Skracamy mianownik po lewej stronie.
   • `1 = 3x - 6`
5. Rozwiązanie: Rozwiązujemy powstałe równanie liniowe.
   • `1 + 6 = 3x`
   • `7 = 3x`
   • `x = 7/3`
6. Sprawdzenie dziedziny: Otrzymane rozwiązanie `x = 7/3` nie jest równe 2, więc należy do dziedziny. Rozwiązanie jest poprawne.

Po uzyskaniu rozwiązania w równaniach wymiernych, zawsze należy sprawdzić, czy otrzymana wartość 'x' należy do wcześniej wyznaczonej dziedziny równania. To absolutnie kluczowy ostatni krok. Jeśli rozwiązanie pokrywa się z wartością wykluczoną z dziedziny, oznacza to, że równanie nie ma rozwiązania lub ma inne rozwiązania, które musimy znaleźć. Ignorowanie dziedziny to jeden z najpoważniejszych błędów w tego typu zadaniach.

Najczęstsze błędy i jak ich unikać

Nawet doświadczonym osobom zdarzają się pomyłki. Przyjrzyjmy się najczęstszym błędom, abyś mógł świadomie weryfikować swoje nawyki i unikać pułapek.

Jednym z najczęstszych błędów jest nieprawidłowe mnożenie, czyli pomnożenie tylko wyrazów ułamkowych, z pominięciem innych składników równania. Pamiętaj, że jeśli mnożymy obie strony równania przez liczbę, to musimy pomnożyć każdy pojedynczy wyraz po obu stronach. Na przykład, w równaniu `1/2x + 3 = 5`, błędem byłoby pomnożenie tylko `1/2x` przez 2. Poprawne podejście to `(1/2x)*2 + 3*2 = 5*2`, co daje `x + 6 = 10`.

Kolejnym źródłem pomyłek są błędy związane z zapominaniem o nawiasach, gdy licznik ułamka jest sumą lub różnicą. Po pomnożeniu przez mianownik, licznik musi być traktowany jako całość. Na przykład, jeśli mamy `(x-1)/2 = 3`, błędem jest zapis `x-1*2=3`. Poprawnie powinniśmy zapisać `(x-1)=3*2`, co prowadzi do `x-1=6` i `x=7`. Dodatkowo, często zdarzają się pomyłki w znakach, zwłaszcza podczas przenoszenia wyrazów na drugą stronę równania (zawsze zmieniamy znak!) lub przy mnożeniu przez liczby ujemne.

Aby ułatwić sobie pracę, zawsze możesz skorzystać z poniższej listy kontrolnej:

1. Sprawdź dziedzinę równania (jeśli x jest w mianowniku): Zawsze zacznij od tego, aby uniknąć błędnych rozwiązań.
2. Znajdź wspólny mianownik (NWW): Jeśli masz wiele ułamków o różnych mianownikach, określ ich NWW.
3. Pomnóż KAŻDY wyraz: Pomnóż każdą stronę i każdy składnik równania przez mianownik (lub NWW).
4. Używaj nawiasów: Jeśli licznik jest sumą lub różnicą, pamiętaj o nawiasach podczas mnożenia.
5. Uprość równanie: Skróć ułamki i wykonaj proste działania.
6. Rozwiąż równanie liniowe: Przenieś niewiadome na jedną stronę, liczby na drugą i wylicz 'x'.
7. Sprawdź znaki: Upewnij się, że nie popełniłeś błędu przy przenoszeniu wyrazów lub mnożeniu przez liczby ujemne.
8. Sprawdź rozwiązanie: Podstaw uzyskane 'x' do pierwotnego równania, aby upewnić się, że jest poprawne i należy do dziedziny.