Upraszczanie sum algebraicznych: Krok po kroku do najprostszej postaci

Witajcie w praktycznym przewodniku, który krok po kroku przeprowadzi Was przez tajniki upraszczania sum algebraicznych. Moim celem jest pokazanie, jak skutecznie redukować wyrazy podobne, poprawnie opuszczać nawiasy i mnożyć wyrażenia, aby zawsze uzyskać najprostszą postać, unikając przy tym typowych błędów, które często kosztują cenne punkty.

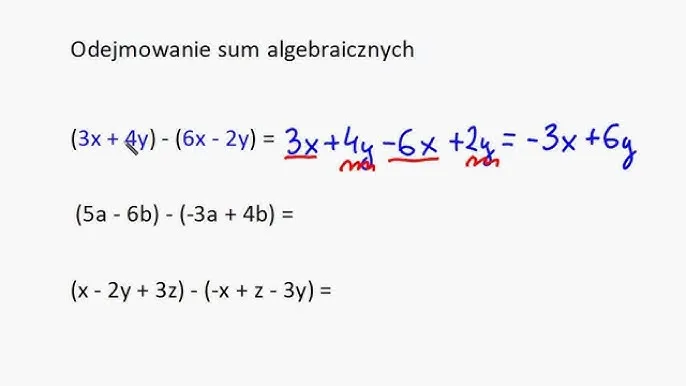
Od czego zacząć? Klucz do zrozumienia sum algebraicznych

Sumy algebraiczne to nic innego jak wyrażenia składające się z jednomianów połączonych znakami dodawania lub odejmowania. Ich upraszczanie jest jedną z fundamentalnych umiejętności w matematyce, stanowiącą bazę do rozwiązywania równań, nierówności, przekształcania wzorów i wielu innych zaawansowanych zagadnień. Bez solidnego opanowania tej sztuki, dalsza nauka algebry staje się znacznie trudniejsza.

Kluczem do upraszczania jest zrozumienie pojęcia "wyrazów podobnych". Są to jednomiany, które mają te same zmienne w tych samych potęgach. Różnić mogą się jedynie współczynnikiem liczbowym, czyli liczbą stojącą przed częścią literową. Część literowa (zmienne wraz z ich potęgami) musi być identyczna. Spójrzmy na przykład: w wyrażeniu 3xy² - 2x + 5xy² - 4, wyrazami podobnymi są 3xy² oraz 5xy². Mają tę samą część literową xy², a różnią się jedynie współczynnikami liczbowymi (3 i 5).

Redukcja wyrazów podobnych: fundament upraszczania wyrażeń

Redukcja wyrazów podobnych to pierwszy i często najważniejszy krok w upraszczaniu sum algebraicznych. To umiejętność, którą każdy powinien opanować do perfekcji. Oto jak to zrobić krok po kroku:

1. Identyfikacja wyrazów podobnych: Przejrzyj całe wyrażenie i znajdź jednomiany, które mają identyczną część literową (te same zmienne w tych samych potęgach). Ja często podkreślam je różnymi kolorami lub symbolami, aby łatwiej je zgrupować. Na przykład, w wyrażeniu 7x + 3y - 2x + 5y, wyrazy podobne to 7x i -2x (mają 'x') oraz 3y i 5y (mają 'y').
2. Grupowanie i działanie na współczynnikach: Gdy już zidentyfikujesz wyrazy podobne, zgrupuj je razem. Następnie wykonaj dodawanie lub odejmowanie wyłącznie na ich współczynnikach liczbowych, zachowując niezmienioną część literową. Dla naszego przykładu:
   • Dla 'x': 7x - 2x = (7 - 2)x = 5x
   • Dla 'y': 3y + 5y = (3 + 5)y = 8y
3. Zapisanie ostatecznego wyniku: Po zredukowaniu wszystkich wyrazów podobnych, zapisz wynik. Wyrazy, które nie miały "pary" (nie były podobne do żadnego innego wyrazu), po prostu przepisujemy bez zmian. W naszym przykładzie ostateczny wynik to 5x + 8y. Pamiętaj, że kolejność wyrazów w sumie nie ma znaczenia, ale zazwyczaj dążymy do uporządkowania ich alfabetycznie lub według potęg.

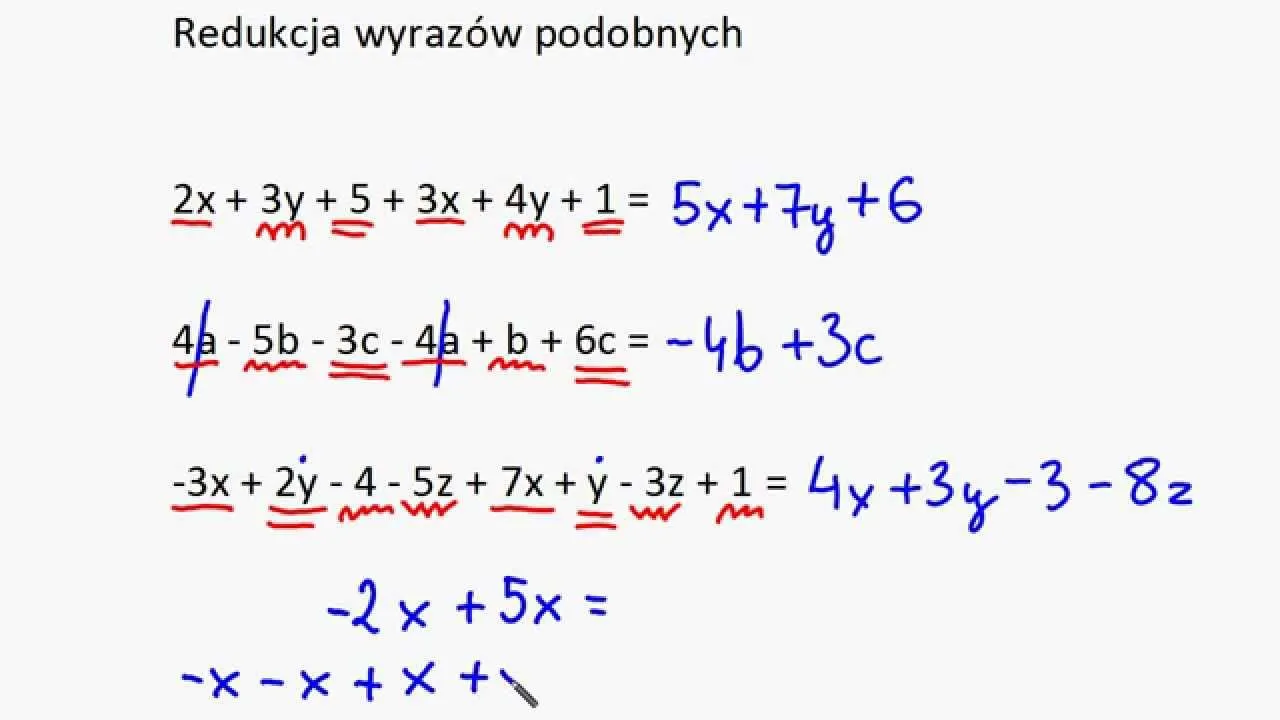
Nawiasy w działaniach: jak sobie z nimi poradzić bez błędów?

Opuszczanie nawiasów to kolejny kluczowy element upraszczania, który często sprawia problemy. Warto zapamiętać trzy podstawowe zasady:

Znak plus (+) przed nawiasem (lub jego brak): Jeśli przed nawiasem stoi znak plus, lub nie ma żadnego znaku (co domyślnie oznacza plus), po prostu opuszczamy nawias, a znaki wszystkich wyrazów wewnątrz pozostają bez zmian. To najprostszy przypadek. Przykład: 5 + (2x - 3) = 5 + 2x - 3 = 2x + 2.

Znak minus (-) przed nawiasem: To jest najczęstsza pułapka! Jeśli przed nawiasem stoi znak minus, opuszczając nawias, musimy zmienić znak każdego wyrazu wewnątrz nawiasu na przeciwny. Jeśli był plus, staje się minus, jeśli był minus, staje się plus. Przykład: 7 - (4y + 2) = 7 - 4y - 2 = -4y + 5.

Liczba przed nawiasem (mnożenie): Gdy przed nawiasem znajduje się liczba (lub jednomian), oznacza to, że należy ją pomnożyć przez każdy wyraz znajdujący się w nawiasie. Pamiętaj o zasadach mnożenia liczb całkowitych i zmiennych. Przykład: 3(x + 4) = 3 * x + 3 * 4 = 3x + 12.

Przechodzimy na wyższy poziom: mnożenie sum algebraicznych

Mnożenie sum algebraicznych, zwłaszcza gdy mamy do czynienia z dwoma nawiasami, wymaga zastosowania zasady "każdy przez każdy". Oznacza to, że każdy wyraz z pierwszego nawiasu musimy pomnożyć przez każdy wyraz z drugiego nawiasu. Dopiero po wykonaniu wszystkich mnożeń przechodzimy do redukcji wyrazów podobnych.

Weźmy na przykład wyrażenie (x + 2)(x - 3). Rozpiszmy to krok po kroku:

(x + 2)(x - 3) =
= x * x (pierwszy wyraz z pierwszego nawiasu razy pierwszy z drugiego)
+ x * (-3) (pierwszy wyraz z pierwszego nawiasu razy drugi z drugiego)
+ 2 * x (drugi wyraz z pierwszego nawiasu razy pierwszy z drugiego)
+ 2 * (-3) (drugi wyraz z pierwszego nawiasu razy drugi z drugiego)

Wykonując mnożenia, otrzymujemy:

x² - 3x + 2x - 6

Po wykonaniu mnożenia, zawsze należy zredukować wyrazy podobne, aby uzyskać najprostszą postać. W tym przypadku wyrazami podobnymi są -3x i +2x:

x² + (-3 + 2)x - 6 = x² - x - 6

Warto również pamiętać o wzorach skróconego mnożenia (kwadrat sumy, kwadrat różnicy, różnica kwadratów). Ich znajomość pozwala znacząco przyspieszyć obliczenia w specyficznych przypadkach, np. (a+b)² czy (a-b)(a+b), ale to temat na osobne, bardziej zaawansowane rozważania. Na początek, zasada "każdy przez każdy" jest uniwersalna i zawsze działa.

Najczęstsze błędy, przez które tracisz punkty i jak ich unikać

Jako Alan Szymczak, widziałem wiele prac i wiem, gdzie najczęściej pojawiają się potknięcia. Oto lista najczęstszych błędów i moje rady, jak ich unikać:

• Pomyłki w znakach: To klasyka, zwłaszcza przy opuszczaniu nawiasów z minusem z przodu. Uczniowie często zmieniają znak tylko pierwszego wyrazu w nawiasie.
  • Rada: Zawsze zmieniaj znak każdego wyrazu w nawiasie. Możesz sobie mentalnie lub na kartce zakreślić każdy wyraz i zmienić jego znak.
• Mylenie wyrazów podobnych: Często widzę, jak uczniowie próbują dodawać x do x² lub xy.
  • Rada: Wyrazy podobne muszą mieć te same zmienne w tych samych potęgach. x to nie to samo co x², a x to nie to samo co xy. Bądź bardzo precyzyjny w identyfikacji.
• Błędy rachunkowe: Zwłaszcza przy operacjach na liczbach ujemnych, np. -3 + 5 czy -2 - 4.
  • Rada: Uważnie sprawdzaj dodawanie i odejmowanie liczb całkowitych. Jeśli masz wątpliwości, użyj osi liczbowej lub pomyśl o długu i spłacie.
• Błędy przy mnożeniu potęg: Niepoprawne dodawanie wykładników, np. x * x = 2x.
  • Rada: Pamiętaj, że x * x = x¹ * x¹ = x¹⁺¹ = x². Mnożąc potęgi o tej samej podstawie, dodajemy wykładniki.

Przeczytaj również: Teselacje i parkietaże: Jak mozaika w matematyce zmienia świat?

Twoja checklista do upraszczania sum algebraicznych

Aby mieć pewność, że zawsze uzyskasz najprostszą postać sumy algebraicznej, postępuj zgodnie z tą listą kontrolną:

1. Krok 1: Opuść nawiasy, pamiętając o znakach. Zastosuj odpowiednie zasady dla plusa, minusa lub liczby przed nawiasem. To kluczowy moment, w którym najłatwiej o błędy.
2. Krok 2: Znajdź i zgrupuj wszystkie wyrazy podobne. Możesz je podkreślać, zaznaczać różnymi kolorami lub symbolami, aby ułatwić sobie zadanie. Upewnij się, że poprawnie identyfikujesz części literowe.
3. Krok 3: Wykonaj działania na współczynnikach wyrazów podobnych i zapisz ostateczny wynik. Pamiętaj o zachowaniu części literowej bez zmian. Uważaj na rachunki, zwłaszcza z liczbami ujemnymi.