Obliczanie wysokości trójkąta to jedno z podstawowych, ale często sprawiających trudność zadań w geometrii. Niezależnie od tego, czy jesteś uczniem, studentem, czy po prostu potrzebujesz odświeżyć swoją wiedzę, ten artykuł będzie Twoim kompleksowym przewodnikiem. Przygotowałem praktyczne instrukcje krok po kroku, które pomogą Ci zrozumieć i zastosować kluczowe metody oraz wzory dla różnych typów trójkątów.
Jak obliczyć wysokość trójkąta kluczowe metody i wzory w pigułce
- Wysokość to odcinek prostopadły z wierzchołka do przeciwległego boku (podstawy), każdy trójkąt ma trzy wysokości.
- Uniwersalny wzór na wysokość, gdy znasz pole (P) i podstawę (a), to: h = (2 * P) / a.
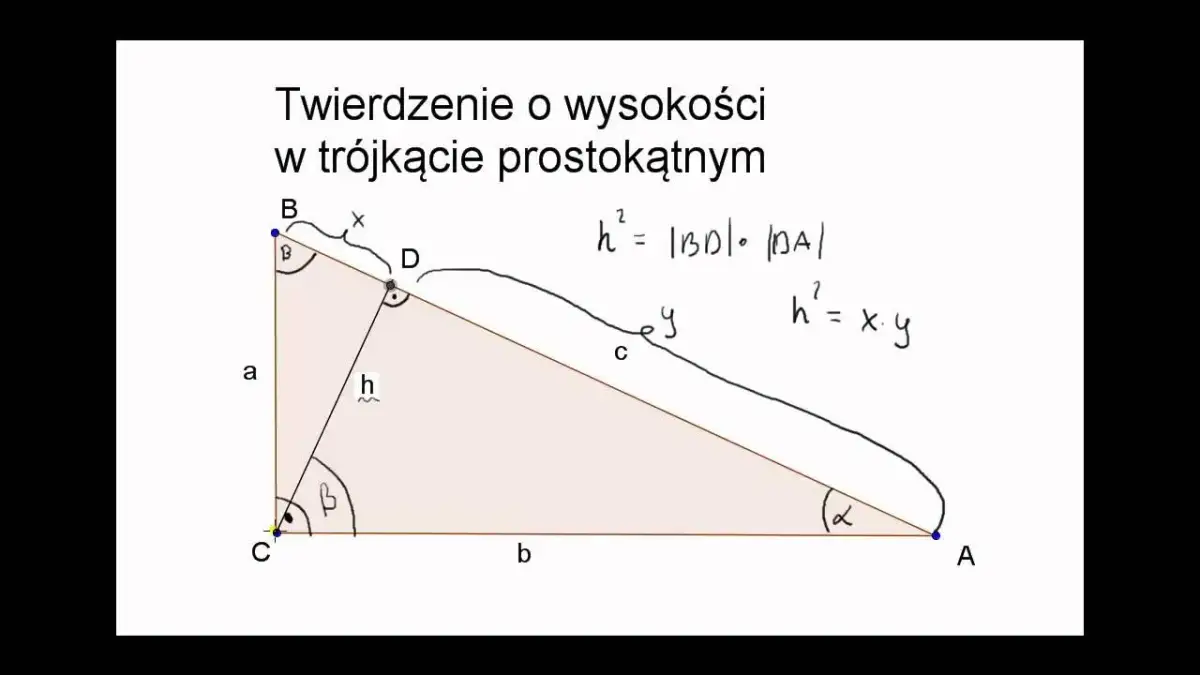
- W trójkącie prostokątnym przyprostokątne są wysokościami, a wysokość na przeciwprostokątną można obliczyć z zależności h² = x * y lub z pola.
- Dla trójkąta równobocznego o boku (a) wysokość wynosi: h = (a√3) / 2.
- W trójkącie równoramiennym wysokość na podstawę obliczysz z twierdzenia Pitagorasa: h = √(a² - (b/2)²).
- W trójkącie różnobocznym najpierw oblicz pole wzorem Herona, a następnie użyj uniwersalnego wzoru na wysokość.
Czym jest wysokość trójkąta i dlaczego jest tak ważna?
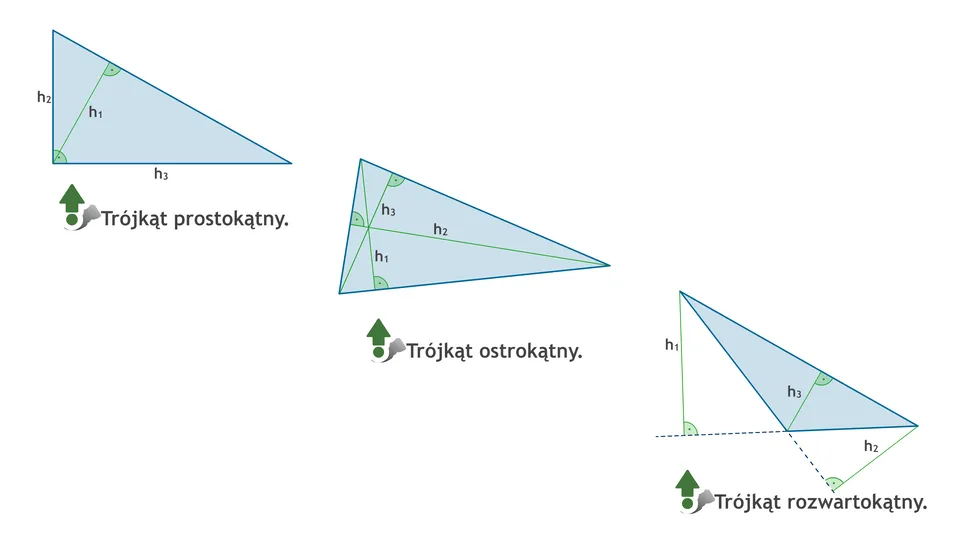
Wysokość trójkąta to nic innego jak odcinek prostopadły, poprowadzony z wierzchołka trójkąta do przeciwległego boku, który nazywamy wówczas podstawą. Co ważne, każdy trójkąt ma aż trzy wysokości, ponieważ możemy je poprowadzić z każdego z trzech wierzchołków. Zazwyczaj oznaczamy je literą "h" z indeksem dolnym odpowiadającym podstawie, np. ha dla wysokości opuszczonej na bok "a".
Ważne jest, aby pamiętać, że wysokość zawsze tworzy kąt prosty z podstawą. W przypadku trójkątów ostrokątnych wszystkie wysokości leżą wewnątrz trójkąta. Jednak w trójkącie rozwartokątnym, wysokości opuszczone na boki tworzące kąt rozwarty, leżą poza trójkątem. Wtedy musimy przedłużyć podstawę, aby wysokość mogła do niej prostopadle dotrzeć. Zrozumienie wysokości jest kluczowe, ponieważ jest ona niezbędna do obliczania pola trójkąta, a także do rozwiązywania wielu innych problemów geometrycznych i trygonometrycznych. Bez niej trudno byłoby mi wyznaczyć wiele innych parametrów figury, dlatego zawsze zwracam na nią szczególną uwagę.
Uniwersalny wzór na wysokość: gdy znasz pole i podstawę
Zacznijmy od najbardziej uniwersalnej metody, która sprawdzi się w każdym trójkącie, niezależnie od jego typu. Jeśli znasz pole trójkąta (P) oraz długość jednej z jego podstaw (a), możesz w prosty sposób obliczyć wysokość (h) opuszczoną na tę podstawę. Wychodzimy od podstawowego wzoru na pole trójkąta: P = (a * h) / 2. Przekształcając ten wzór, aby wyznaczyć wysokość, otrzymujemy:
h = (2 * P) / a
To naprawdę potężne narzędzie, które pozwala mi szybko znaleźć wysokość, gdy inne dane są już dostępne. Spójrzmy na przykład:
- Załóżmy, że pole trójkąta wynosi 24 cm².
- Długość jego podstawy to 8 cm.
- Aby obliczyć wysokość, podstawiamy dane do wzoru: h = (2 * 24 cm²) / 8 cm.
- h = 48 cm² / 8 cm.
- h = 6 cm.
Proste, prawda? Ten wzór to podstawa, którą zawsze warto mieć w pamięci.
Wysokość w trójkącie prostokątnym: proste metody
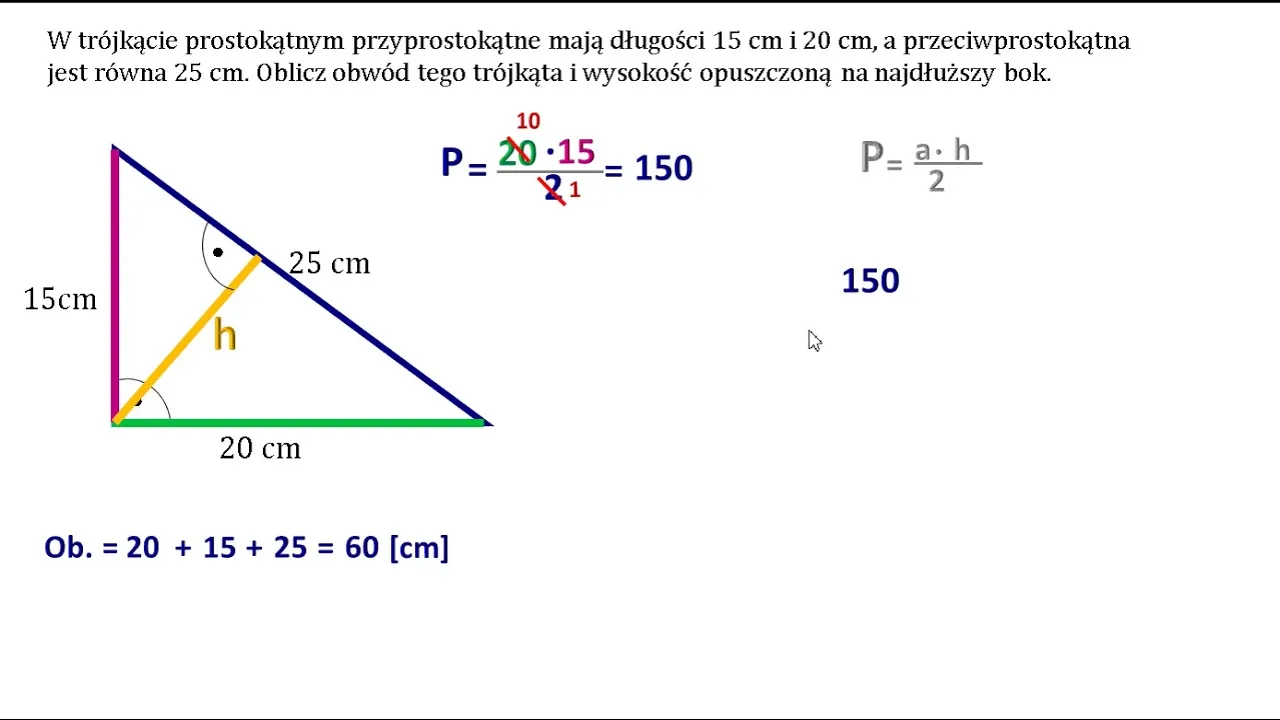
Trójkąt prostokątny jest wyjątkowy pod wieloma względami. Przede wszystkim, dwie przyprostokątne są jednocześnie wysokościami tego trójkąta. Oznacza to, że wysokość opuszczona na jedną przyprostokątną to po prostu długość drugiej przyprostokątnej. To znacznie upraszcza sprawę! Jednak często musimy obliczyć trzecią wysokość tę opuszczoną na przeciwprostokątną.
Istnieją dwie główne metody, aby to zrobić:
Metoda 1: Wykorzystując wzór na pole
Jeśli znamy długości obu przyprostokątnych (a i b) oraz przeciwprostokątnej (c), możemy wykorzystać fakt, że pole trójkąta prostokątnego można obliczyć na dwa sposoby: P = (a * b) / 2 lub P = (c * h) / 2. Przyrównując te wzory, otrzymujemy: a * b = c * h. Stąd wzór na wysokość opuszczoną na przeciwprostokątną (h) to: h = (a * b) / c.
Przykład: Jeśli przyprostokątne mają długość 6 cm i 8 cm, a przeciwprostokątna 10 cm, to h = (6 * 8) / 10 = 48 / 10 = 4,8 cm.
Metoda 2: Z zależności geometrycznej (twierdzenie o wysokości w trójkącie prostokątnym)
Wysokość opuszczona na przeciwprostokątną dzieli ją na dwa odcinki, które często oznaczamy jako x i y. Istnieje prosta zależność: h² = x * y. To bardzo przydatne, gdy znamy długości tych odcinków. Pamiętam, jak często korzystałem z tego w zadaniach, gdzie brakowało mi innych danych.
Przykład: Jeśli wysokość dzieli przeciwprostokątną na odcinki o długości 4 cm i 9 cm, to h² = 4 * 9 = 36. Zatem h = √36 = 6 cm.
Trójkąt równoboczny: szybkie obliczanie wysokości
Trójkąt równoboczny to marzenie każdego, kto musi obliczać wysokości! Wszystkie jego boki są równe (oznaczmy je jako 'a'), a co za tym idzie, wszystkie trzy wysokości również są równe. Wyprowadzenie wzoru jest dość proste i opiera się na twierdzeniu Pitagorasa. Jeśli podzielimy trójkąt równoboczny wysokością na dwie identyczne połówki, otrzymamy dwa trójkąty prostokątne. Jeden z boków takiego trójkąta to 'a', drugi to 'h', a trzeci to 'a/2'. Zgodnie z twierdzeniem Pitagorasa: h² + (a/2)² = a². Po przekształceniu otrzymujemy bardzo użyteczny wzór:
h = (a√3) / 2
Ten wzór pozwala mi błyskawicznie obliczyć wysokość, znając tylko długość boku. To ogromna oszczędność czasu!
Przykład: Jeśli bok trójkąta równobocznego ma długość 10 cm, to h = (10√3) / 2 = 5√3 cm.
Wysokość w trójkącie równoramiennym: krok po kroku
W trójkącie równoramiennym dwa boki (ramiona) mają tę samą długość (oznaczmy je jako 'a'), a trzeci bok to podstawa (oznaczmy ją jako 'b'). Najczęściej obliczamy wysokość opuszczoną na podstawę 'b'. Ta wysokość ma szczególną właściwość: dzieli podstawę na dwa równe odcinki, każdy o długości b/2. Tworzy to dwa identyczne trójkąty prostokątne, gdzie przeciwprostokątną jest ramię 'a', jedną przyprostokątną jest wysokość 'h', a drugą połowa podstawy 'b/2'.
Korzystając z twierdzenia Pitagorasa, możemy zapisać: h² + (b/2)² = a². Przekształcając ten wzór, otrzymujemy:
h = √(a² - (b/2)²)
Warto również pamiętać, że wysokości opuszczone na ramiona w trójkącie równoramiennym są równej długości, ale ich obliczenie jest nieco bardziej złożone i zazwyczaj wymaga użycia wzoru na pole (o którym pisałem wcześniej) lub funkcji trygonometrycznych.
Oto szczegółowy przykład obliczeń dla wysokości opuszczonej na podstawę:
- Mamy trójkąt równoramienny o ramionach a = 13 cm i podstawie b = 10 cm.
- Wysokość dzieli podstawę na dwa odcinki: b/2 = 10 cm / 2 = 5 cm.
- Teraz stosujemy twierdzenie Pitagorasa: h² + 5² = 13².
- h² + 25 = 169.
- h² = 169 - 25.
- h² = 144.
- h = √144.
- h = 12 cm.
Trójkąt różnoboczny: wysokość z wykorzystaniem wzoru Herona
Trójkąt różnoboczny to najbardziej wymagający przypadek, gdy znamy tylko długości trzech boków (a, b, c), a nie mamy informacji o kątach czy polu. W takiej sytuacji nie możemy od razu zastosować prostych wzorów. Moją sprawdzoną metodą jest najpierw obliczenie pola trójkąta za pomocą wzoru Herona, a następnie wykorzystanie tego pola do wyznaczenia wysokości. To dwuetapowy proces, ale bardzo skuteczny.
Oto jak to zrobić krok po kroku:
-
Oblicz połowę obwodu (p) trójkąta.
p = (a + b + c) / 2
Przykład: Jeśli boki to a=7 cm, b=8 cm, c=9 cm, to p = (7 + 8 + 9) / 2 = 24 / 2 = 12 cm. -
Oblicz pole trójkąta (P) ze wzoru Herona.
P = √[p(p-a)(p-b)(p-c)]
Kontynuując przykład: P = √[12(12-7)(12-8)(12-9)] = √[12 * 5 * 4 * 3] = √[720].
P ≈ 26,83 cm². -
Wykorzystaj obliczone pole do znalezienia każdej z trzech wysokości.
Teraz, gdy znamy pole, możemy wrócić do uniwersalnego wzoru h = (2 * P) / podstawa.
Dla wysokości opuszczonej na bok 'a' (ha): ha = (2 * P) / a
Dla wysokości opuszczonej na bok 'b' (hb): hb = (2 * P) / b
Dla wysokości opuszczonej na bok 'c' (hc): hc = (2 * P) / c
Kontynuując przykład:
ha = (2 * 26,83) / 7 ≈ 53,66 / 7 ≈ 7,67 cm.
hb = (2 * 26,83) / 8 ≈ 53,66 / 8 ≈ 6,71 cm.
hc = (2 * 26,83) / 9 ≈ 53,66 / 9 ≈ 5,96 cm.
Jak widać, ten proces wymaga nieco więcej kroków, ale jest niezawodny, gdy mamy do czynienia z trójkątem różnobocznym i znamy tylko jego boki.
Częste błędy i jak ich unikać przy obliczaniu wysokości
W mojej praktyce widzę, że nawet doświadczeni potrafią popełnić proste błędy przy obliczaniu wysokości trójkąta. Oto najczęstsze pułapki i moje wskazówki, jak ich unikać:
- Mylenie wzorów dla różnych typów trójkątów: To chyba najczęstszy błąd. Wzór na wysokość w trójkącie równobocznym (h = (a√3) / 2) jest specyficzny tylko dla niego. Nie próbuj go stosować w trójkącie równoramiennym czy różnobocznym! Zawsze upewnij się, z jakim typem trójkąta masz do czynienia, zanim wybierzesz wzór.
- Błędne stosowanie twierdzenia Pitagorasa: Twierdzenie Pitagorasa (a² + b² = c²) dotyczy tylko trójkątów prostokątnych. Upewnij się, że trójkąt, w którym go stosujesz, jest faktycznie prostokątny lub że wyodrębniłeś z większego trójkąta taki prostokątny fragment (np. wysokość tworząca trójkąt prostokątny z ramieniem i połową podstawy). Pamiętaj też, że 'c' zawsze oznacza przeciwprostokątną, czyli najdłuższy bok leżący naprzeciw kąta prostego.
- Zapominanie, że wysokość może leżeć poza trójkątem (w trójkącie rozwartokątnym): To bardzo ważna kwestia. W trójkątach rozwartokątnych, wysokości opuszczone na boki tworzące kąt rozwarty, spadają na przedłużenie podstawy. Wizualizacja tego jest kluczowa. Jeśli masz wątpliwości, zawsze narysuj trójkąt i jego wysokości to często pomaga uniknąć błędu.
Przeczytaj również: Działania odwrotne: Twoja supermoc w matematyce! Rozwiąż równania
Szybka ściągawka: najważniejsze wzory na wysokość trójkąta
Aby ułatwić Ci zapamiętanie i szybkie odnalezienie potrzebnych informacji, przygotowałem krótką tabelę podsumowującą najważniejsze wzory na wysokość trójkąta. Mam nadzieję, że będzie to dla Ciebie przydatna ściągawka!
| Typ trójkąta | Dane wejściowe | Wzór na wysokość |
|---|---|---|
| Uniwersalny (dowolny) | Pole (P), Podstawa (a) | h = (2 * P) / a |
| Prostokątny | Przyprostokątne (a, b), Przeciwprostokątna (c) | hc = (a * b) / c (wysokość na przeciwprostokątną) |
| Prostokątny | Odcinki przeciwprostokątnej (x, y) | hc = √(x * y) (wysokość na przeciwprostokątną) |
| Równoboczny | Długość boku (a) | h = (a√3) / 2 |
| Równoramienny | Ramię (a), Podstawa (b) | hb = √(a² - (b/2)²) (wysokość na podstawę) |
| Różnoboczny | Boki (a, b, c) | 1. p = (a+b+c)/2 2. P = √[p(p-a)(p-b)(p-c)] 3. ha = (2*P)/a (i analogicznie dla hb, hc) |