W świecie matematyki, gdzie liczby i kształty splatają się w fascynujące wzory, sinus jest jednym z tych pojęć, które na początku mogą wydawać się abstrakcyjne, ale w rzeczywistości są fundamentalne dla zrozumienia otaczającego nas świata. Jako Alan Szymczak, z mojego doświadczenia wiem, że wiele osób, zwłaszcza uczniów, boryka się z jego zrozumieniem. Dlatego przygotowałem ten artykuł, aby wyjaśnić, czym jest sinus jedna z podstawowych funkcji trygonometrycznych. Dowiesz się z niego, jak działa sinus w trójkącie prostokątnym, jak rozszerzyć jego definicję na dowolny kąt oraz gdzie spotkać go w codziennym życiu, od fal dźwiękowych po GPS. To kompleksowy przewodnik, który pomoże Ci zrozumieć to kluczowe pojęcie matematyczne od podstaw.
Sinus to stosunek w trójkącie prostokątnym i współrzędna y na okręgu jednostkowym
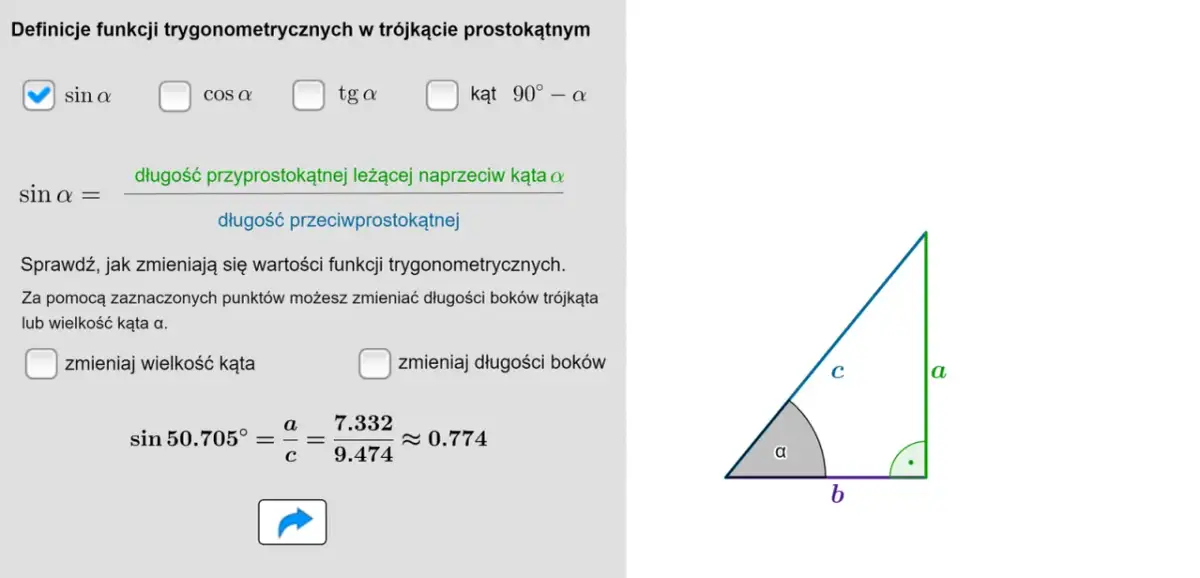
- Sinus kąta ostrego w trójkącie prostokątnym to stosunek długości przyprostokątnej leżącej naprzeciw kąta do długości przeciwprostokątnej.
- Dla dowolnego kąta sinus to współrzędna y punktu przecięcia ramienia kąta z okręgiem jednostkowym.
- Wykres funkcji sinus to falista sinusoida, która powtarza się co 360° (2π radianów).
- Wartości sinusa zawsze mieszczą się w przedziale od -1 do 1.
- Sinus jest kluczowy do opisu zjawisk falowych i okresowych w fizyce, technice i wielu innych dziedzinach.
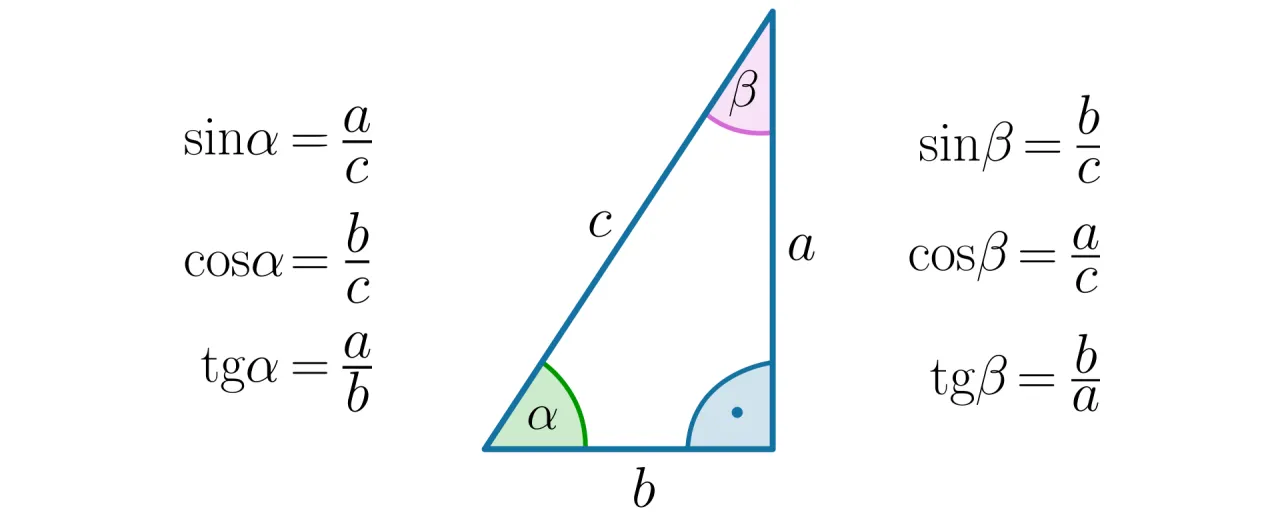
Czym jest sinus? Pierwsze kroki w trójkącie prostokątnym
Najprostsza definicja: Skąd bierze się sinus?
Zacznijmy od podstaw, czyli od trójkąta prostokątnego. To właśnie tutaj sinus ma swoją najprostszą i najbardziej intuicyjną definicję. Sinus (skrót: sin) kąta ostrego w trójkącie prostokątnym to nic innego jak stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej. Innymi słowy, jeśli wybierzemy jeden z kątów ostrych, sinus powie nam, jak długa jest "przeciwna" przyprostokątna w stosunku do najdłuższego boku, czyli przeciwprostokątnej. Jest to jedna z trzech podstawowych funkcji trygonometrycznych, obok cosinusa i tangensa, które pozwalają nam opisywać relacje między kątami a długościami boków w trójkątach prostokątnych.Jak w 3 krokach obliczyć sinus kąta ostrego? Praktyczny przykład
Aby to dobrze zrozumieć, przyjrzyjmy się prostemu przykładowi. Wyobraźmy sobie trójkąt prostokątny o bokach długości 3, 4 i 5. Wiemy, że najdłuższy bok (5) to przeciwprostokątna. Załóżmy, że chcemy obliczyć sinus kąta α, który leży naprzeciwko boku o długości 3.
- Zidentyfikuj boki: W naszym trójkącie przeciwprostokątna ma długość 5, a przyprostokątna leżąca naprzeciw kąta α ma długość 3.
- Zastosuj definicję: Sinus kąta α to stosunek długości przyprostokątnej leżącej naprzeciw kąta do długości przeciwprostokątnej.
- Wykonaj obliczenia: Zatem sin(α) = 3/5 = 0.6. To proste!
Dlaczego rozmiar trójkąta nie zmienia wartości sinusa?
To bardzo ważne spostrzeżenie, które często zaskakuje początkujących. Wartość sinusa danego kąta ostrego jest zawsze stała, niezależnie od tego, jak duży lub mały jest trójkąt prostokątny, w którym ten kąt występuje. Dlaczego tak się dzieje? Odpowiedzią jest pojęcie podobieństwa trójkątów. Jeśli mamy dwa trójkąty prostokątne, które mają takie same kąty (a więc są podobne), to stosunki odpowiadających sobie boków są zawsze takie same. Oznacza to, że jeśli powiększymy lub pomniejszymy trójkąt, zachowując jego kąty, długości boków zmienią się proporcjonalnie, ale ich stosunki w tym stosunek przyprostokątnej do przeciwprostokątnej pozostaną niezmienione. To właśnie ta niezmienność sprawia, że sinus jest tak potężnym narzędziem w matematyce i inżynierii.
Sinus dla każdego kąta: odkryj okrąg jednostkowy
Okrąg jednostkowy klucz do zrozumienia trygonometrii
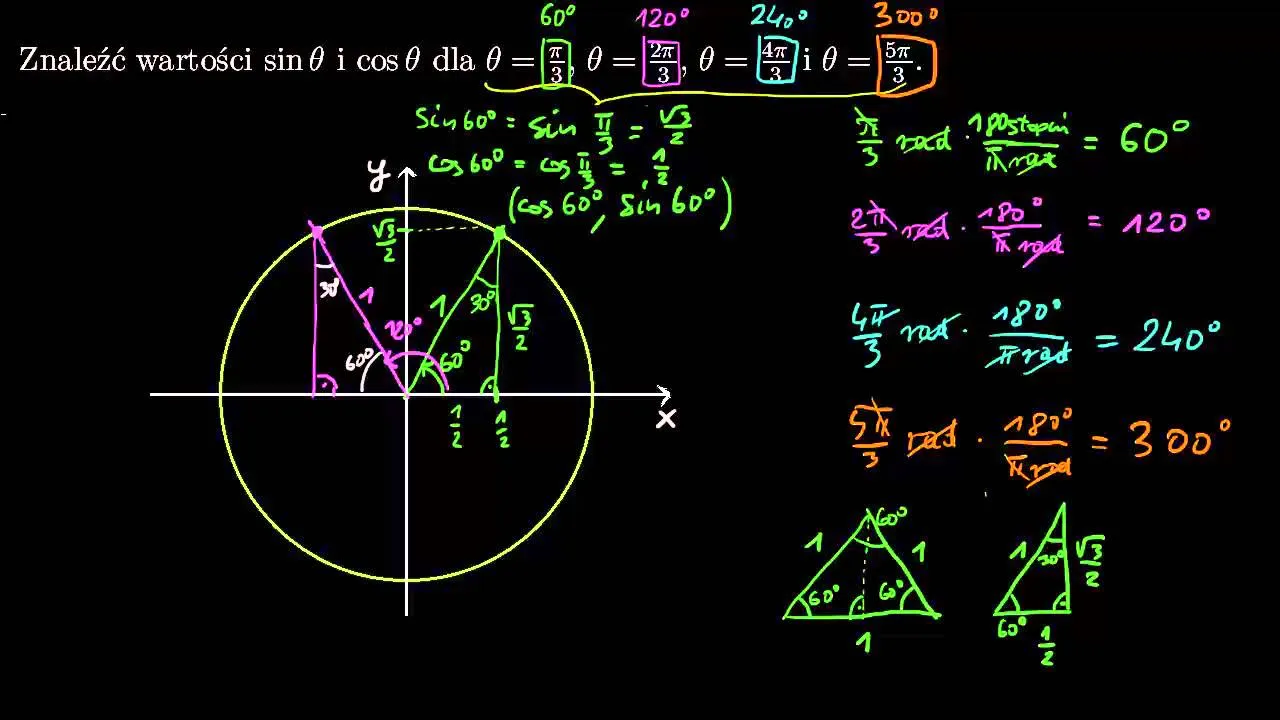
Definicja sinusa w trójkącie prostokątnym jest świetnym punktem wyjścia, ale co, jeśli chcemy obliczyć sinus kąta większego niż 90 stopni, na przykład 120 stopni czy 270 stopni? Tutaj z pomocą przychodzi nam okrąg jednostkowy. Wyobraź sobie okrąg o promieniu równym 1, którego środek znajduje się w początku układu współrzędnych (0,0). Kąt α mierzymy od dodatniej półosi X, obracając się przeciwnie do ruchu wskazówek zegara. Drugie ramię kąta α przetnie okrąg w pewnym punkcie (x, y). I tu jest klucz: wartość sinusa kąta α to po prostu współrzędna y tego punktu przecięcia. To uogólnienie pozwala nam rozszerzyć definicję sinusa na dowolny kąt, w tym kąty ujemne czy większe niż 360 stopni.
Jak odczytać wartość sinusa w układzie współrzędnych?
Odczytywanie wartości sinusa z okręgu jednostkowego jest stosunkowo proste, gdy już zrozumiesz jego zasadę. Po prostu narysuj kąt α, zaczynając od dodatniej półosi X. Punkt, w którym ramię końcowe kąta przecina okrąg jednostkowy, ma swoje współrzędne (x, y). Współrzędna y tego punktu to wartość sinusa kąta α. Na przykład, dla kąta 90 stopni, ramię końcowe leży na dodatniej półosi Y, a punkt przecięcia to (0, 1). Zatem sin(90°) = 1. Dla kąta 180 stopni, punkt to (-1, 0), więc sin(180°) = 0. To wizualne podejście, moim zdaniem, bardzo pomaga w zrozumieniu, jak sinus zmienia się wraz z kątem.
Dodatni czy ujemny? Odkryj, jak zmienia się znak sinusa w ćwiartkach
Korzystając z okręgu jednostkowego, łatwo zauważyć, jak zmienia się znak sinusa w zależności od ćwiartki, w której znajduje się ramię końcowe kąta:
- I ćwiartka (od 0° do 90°): Współrzędna y jest dodatnia, więc sinus jest dodatni.
- II ćwiartka (od 90° do 180°): Współrzędna y jest nadal dodatnia, więc sinus jest dodatni.
- III ćwiartka (od 180° do 270°): Współrzędna y jest ujemna, więc sinus jest ujemny.
- IV ćwiartka (od 270° do 360°): Współrzędna y jest ujemna, więc sinus jest ujemny.
Ta wiedza jest kluczowa przy rozwiązywaniu równań trygonometrycznych i analizowaniu zachowania funkcji sinus.
Funkcja sinus i jej wykres: poznaj sinusoidę
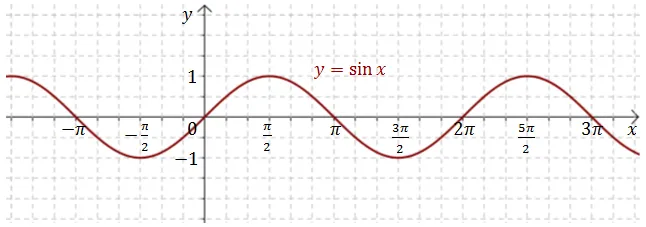
Czym jest sinusoida i dlaczego przypomina falę?
Jeśli naniesiemy wartości sinusa dla kolejnych kątów na wykres, gdzie oś X reprezentuje kąt (zazwyczaj w radianach, ale może być też w stopniach), a oś Y wartość sinusa, otrzymamy charakterystyczną krzywą zwaną sinusoidą. Jest to piękna, falista linia, która wznosi się i opada w regularny sposób. Jej falisty kształt nie jest przypadkowy odzwierciedla on okresowy charakter funkcji sinus. To właśnie dzięki temu kształtowi sinusoida jest tak niezastąpiona w opisie wszelkich zjawisk okresowych w przyrodzie i technice, od fal dźwiękowych po prąd przemienny. Widzę w niej matematyczną elegancję, która łączy abstrakcję z rzeczywistością.
Najważniejsze cechy funkcji sinus: dziedzina, wartości i okresowość
Funkcja sinus, oznaczana jako y = sin(x), ma kilka kluczowych właściwości, które warto znać:
- Dziedzina: Zbiór wszystkich liczb rzeczywistych (R). Oznacza to, że możemy obliczyć sinus dla dowolnego kąta dodatniego, ujemnego, zerowego, czy nawet bardzo dużego.
- Zbiór wartości: Przedział domknięty [-1, 1]. To oznacza, że wartość sinusa nigdy nie wyjdzie poza ten zakres. Zawsze będzie się mieścić między -1 a 1 włącznie.
- Okres podstawowy: 2π (co odpowiada 360°). Ta właściwość oznacza, że wykres funkcji powtarza się co każde 2π (lub 360°). Po prostu, sin(x) = sin(x + 2πk), gdzie k jest dowolną liczbą całkowitą.
- Funkcja nieparzysta: sin(-x) = -sin(x). Jest to symetria względem początku układu współrzędnych.
Miejsca zerowe i ekstrema, czyli gdzie sinus osiąga 0, 1 i -1
Z punktu widzenia sinusoidy, miejsca zerowe to punkty, w których krzywa przecina oś X. Dla funkcji sinus, dzieje się to, gdy kąt jest wielokrotnością π (lub 180°). Zatem miejsca zerowe funkcji sinus to x = kπ, gdzie k jest dowolną liczbą całkowitą (np. 0, π, 2π, -π itd.). Natomiast ekstrema, czyli wartości maksymalne i minimalne, sinus osiąga w konkretnych punktach. Wartość maksymalna, czyli 1, pojawia się dla kątów takich jak π/2 (90°), 5π/2 (450°) i tak dalej. Wartość minimalna, czyli -1, występuje dla kątów takich jak 3π/2 (270°), 7π/2 (630°) itd. Zawsze pamiętajmy, że te wartości mieszczą się w zbiorze wartości [-1, 1], o którym wspomniałem wcześniej.
Sinus w praktyce: obliczenia i zastosowania
Kluczowe wartości, które warto zapamiętać (0°, 30°, 45°, 60°, 90°)
Chociaż kalkulatory są powszechne, warto znać wartości sinusa dla kilku kluczowych kątów. Są one często wykorzystywane w zadaniach i stanowią dobry punkt odniesienia. Oto tabela, którą, z mojego doświadczenia, warto mieć zawsze pod ręką:
| Kąt | Wartość sinusa |
|---|---|
| 0° | 0 |
| 30° | 1/2 |
| 45° | √2/2 |
| 60° | √3/2 |
| 90° | 1 |
Zapamiętanie tych wartości znacznie przyspieszy wiele obliczeń.
Czym jest "jedynka trygonometryczna" i dlaczego jest tak ważna?
W trygonometrii istnieje wzór, który jest absolutnie fundamentalny i nazywany jest "jedynką trygonometryczną". Brzmi on: sin²(α) + cos²(α) = 1. Ten wzór mówi nam, że kwadrat sinusa dowolnego kąta plus kwadrat cosinusa tego samego kąta zawsze równa się 1. Jest to bezpośrednia konsekwencja twierdzenia Pitagorasa zastosowanego do okręgu jednostkowego. Jego znaczenie jest ogromne pozwala nam na łatwe przekształcanie wyrażeń trygonometrycznych, obliczanie jednej funkcji, gdy znamy drugą, i jest podstawą wielu bardziej złożonych tożsamości. To prawdziwy kamień węgielny trygonometrii.
Jak kalkulator oblicza sinus? Metody i narzędzia
Zastanawialiście się kiedyś, jak kalkulator naukowy lub komputer oblicza sinus kąta? Nie mierzy on trójkątów ani nie rysuje okręgów jednostkowych! Zamiast tego, wykorzystuje zaawansowane algorytmy, najczęściej rozwinięcia w szeregi potęgowe (szereg Taylora lub Maclaurina). Te szeregi pozwalają przybliżyć wartość funkcji sinus za pomocą sumy nieskończonej liczby wyrazów. Im więcej wyrazów zostanie użytych, tym dokładniejszy wynik. Na szczęście, w dzisiejszych czasach nie musimy znać tych skomplikowanych metod. Wystarczy, że mamy pod ręką kalkulator naukowy, smartfon z aplikacją matematyczną lub dostęp do narzędzi online, które błyskawicznie podają nam potrzebne wartości sinusa.
Sinus wokół nas: zaskakujące zastosowania
Od fal dźwiękowych po prąd w gniazdku: Sinus w fizyce i technice
Sinus i jego falisty wykres, czyli sinusoida, są wszechobecne w świecie fizyki i inżynierii. To naprawdę fascynujące, jak abstrakcyjne pojęcie matematyczne znajduje tak wiele praktycznych zastosowań:
- Fale dźwiękowe: Dźwięk rozchodzi się w postaci fal, a najprostszy, czysty ton (np. z kamertonu) może być idealnie opisany przez sinusoidę.
- Fale elektromagnetyczne: Światło, fale radiowe, mikrofale wszystkie te formy energii rozchodzą się jako fale elektromagnetyczne, których kształt jest sinusoidalny.
- Prąd przemienny (AC): Prąd, który płynie w naszych gniazdkach, to właśnie prąd przemienny. Jego napięcie zmienia się w czasie w sposób sinusoidalny. Mówi się o "czystym sinusie" w kontekście zasilaczy, co oznacza idealnie gładką sinusoidę, pożądaną dla wrażliwych urządzeń elektronicznych.
- Drgania mechaniczne i ruch harmoniczny: Wahadło zegara, sprężyna z obciążeniem ruch tych obiektów, jeśli nie ma dużych oporów, jest ruchem harmonicznym, który opisuje się za pomocą funkcji sinus.
Jak GPS używa sinusa do określania Twojej lokalizacji?
Czy wiedziałeś, że sinus pomaga Ci znaleźć drogę? Systemy nawigacji satelitarnej, takie jak GPS, polegają na precyzyjnym pomiarze odległości od kilku satelitów do odbiornika na Ziemi. Proces ten, zwany triangulacją (lub trilateracją), wykorzystuje trygonometrię, w tym funkcje sinus i cosinus, do obliczenia dokładnej pozycji. Satelity wysyłają sygnały, które są odbierane przez Twoje urządzenie. Na podstawie różnic w czasie dotarcia tych sygnałów i znanej pozycji satelitów, algorytmy trygonometryczne obliczają Twoje współrzędne geograficzne. Bez sinusa i cosinusa, precyzyjne określenie Twojej lokalizacji byłoby niemożliwe.
Sinus w grafice komputerowej, muzyce i medycynie: zaskakujące przykłady
Zastosowania sinusa wykraczają daleko poza fizykę i nawigację. Oto kilka przykładów, które często zaskakują:
- Grafika komputerowa i gry: Aby stworzyć płynne animacje, efekty falowania wody, ruch kamer czy realistyczne oświetlenie, programiści często wykorzystują funkcje sinus i cosinus. Pozwalają one na generowanie powtarzalnych, naturalnie wyglądających ruchów.
- Muzyka i akustyka: Analiza dźwięku, synteza muzyki, tworzenie efektów specjalnych wszędzie tam, gdzie mamy do czynienia z falami dźwiękowymi, sinus jest kluczowy. Czysty ton, jak już wspomniałem, to idealna sinusoida.
- Medycyna: W analizie sygnałów biologicznych, takich jak elektrokardiogram (EKG) mierzący aktywność serca czy elektroencefalogram (EEG) mierzący aktywność mózgu, funkcje trygonometryczne pomagają w rozkładaniu złożonych sygnałów na prostsze składowe sinusoidalne, co ułatwia diagnozę.
Sinus i inne funkcje trygonometryczne: poznaj ich relacje
Braterska relacja: Czym sinus różni się od cosinusa?
Sinus i cosinus są jak rodzeństwo bardzo blisko ze sobą związane, ale mające swoje unikalne cechy. W trójkącie prostokątnym, o ile sinus to stosunek przyprostokątnej naprzeciwległej do przeciwprostokątnej, o tyle cosinus to stosunek przyprostokątnej przyległej do przeciwprostokątnej. Na okręgu jednostkowym różnica jest jeszcze bardziej widoczna: sinus to współrzędna y, a cosinus to współrzędna x punktu przecięcia ramienia kąta z okręgiem. Ich wykresy są identyczne, ale przesunięte względem siebie w fazie o 90 stopni (π/2 radianów). Oznacza to, że wykres cosinusa wygląda jak wykres sinusa, ale "startuje" 90 stopni wcześniej. Ta braterska relacja jest kluczowa dla całej trygonometrii.
Przeczytaj również: Symbole matematyczne: Co oznaczają? Jasne wyjaśnienia