Oblicz podstawę logarytmu: Opanuj to w 3 krokach! Przykłady.

Często spotykam się z pytaniem, jak obliczyć podstawę logarytmu, gdy jest ona niewiadomą. To klasyczne zadanie, które na pierwszy rzut oka może wydawać się skomplikowane, ale w rzeczywistości sprowadza się do zrozumienia jednej kluczowej definicji i kilku prostych kroków. W tym artykule, jako Alan Szymczak, przeprowadzę Cię przez cały proces, dostarczając jasnych instrukcji, niezbędnych wzorów i praktycznych przykładów. Moim celem jest, abyś po lekturze bez problemu potrafił rozwiązać każde zadanie polegające na znalezieniu niewiadomej podstawy logarytmu.

Zrozumienie logarytmu to klucz do łatwego obliczania podstawy

Zanim przejdziemy do konkretnych obliczeń, musimy sobie uświadomić, czym tak naprawdę jest logarytm. W gruncie rzeczy, logarytm to nic innego jak inny sposób zapisu potęgi. Gdy tylko zrozumiesz tę fundamentalną zależność, cała reszta stanie się znacznie prostsza. To właśnie ta idea stanowi fundament do skutecznego obliczania niewiadomej podstawy logarytmu.

Klucz do sukcesu: jedna prosta zasada, która zmienia wszystko

Najważniejszą zasadą, którą musisz opanować, jest definicja logarytmu. To ona pozwala nam przekształcić zapis logarytmiczny na potęgowy, co jest absolutnie kluczowe w procesie obliczania podstawy. Zapamiętaj ten wzór, bo to on otwiera drzwi do rozwiązania:

logₐb = c ⇔ aᶜ = b

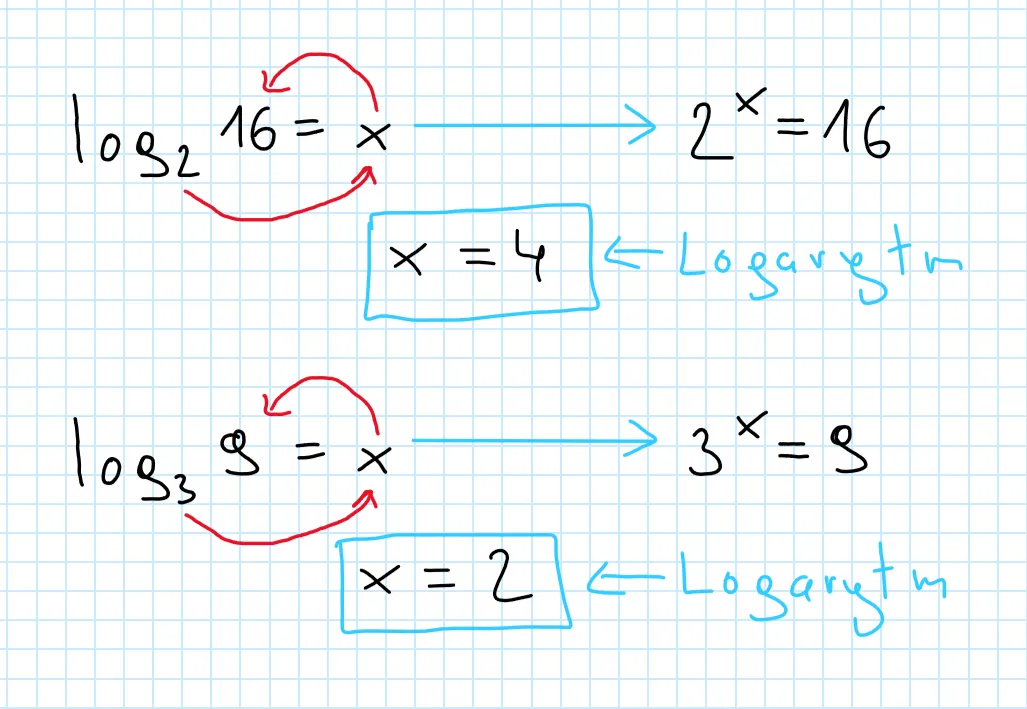
Jak czytać zapis logₐb = c, by od razu wiedzieć, o co chodzi?

Aby swobodnie posługiwać się logarytmami, warto wiedzieć, co oznaczają poszczególne elementy w zapisie logₐb = c. Każdy z nich ma swoją rolę i konkretną nazwę w polskiej terminologii matematycznej:

• a to podstawa logarytmu. Jest to liczba, którą podnosimy do potęgi. W naszym przypadku, to właśnie ją będziemy szukać.
• b to liczba logarytmowana. Jest to wynik potęgowania, czyli liczba, którą chcemy otrzymać.
• c to wynik logarytmu (lub wartość logarytmu). Jest to wykładnik potęgi, do której należy podnieść podstawę 'a', aby otrzymać liczbę 'b'.

Zrozumienie tych ról pozwala na intuicyjne przekształcanie równań.

Przekształć logarytm w potęgę i odkryj najważniejszy wzór

Skoro już wiemy, czym jest logarytm i jak czytać jego zapis, czas przejść do sedna, czyli do praktycznego zastosowania definicji. Kluczowym krokiem w obliczaniu podstawy logarytmu jest jego przekształcenie w równanie potęgowe. To właśnie w tej formie będziemy w stanie wyznaczyć naszą niewiadomą 'a'.

Definicja logarytmu w praktyce: przekształcenie krok po kroku

Proces przekształcania równania logarytmicznego na potęgowe jest prosty i zawsze przebiega tak samo. Oto jak to zrobić:

1. Zapisz równanie logarytmiczne: Zaczynamy od równania w postaci logₐb = c.
2. Zidentyfikuj elementy: Określ, co jest podstawą (a), co liczbą logarytmowaną (b), a co wynikiem (c).
3. Przekształć na formę potęgową: Zgodnie z definicją logarytmu (logₐb = c ⇔ aᶜ = b), zapisz równanie w postaci aᶜ = b.

Na przykład, jeśli mamy logₐ16 = 2, przekształcamy to na a² = 16. To jest właśnie ten moment, w którym logarytm staje się równaniem potęgowym, które znacznie łatwiej rozwiązać.

Od równania do wyniku: techniki rozwiązywania z niewiadomą 'a' w podstawie

Po przekształceniu równania logarytmicznego na potęgowe (aᶜ = b), naszym zadaniem jest wyznaczenie 'a'. Najczęściej sprowadza się to do podniesienia obu stron równania do potęgi, która jest odwrotnością wykładnika 'c'. Innymi słowy, jeśli mamy aᶜ = b, to aby wyznaczyć 'a', podnosimy obie strony do potęgi 1/c:

a = b^(1/c)

W praktyce oznacza to często pierwiastkowanie. Jeśli np. c=2, to pierwiastkujemy kwadratowo; jeśli c=3, to pierwiastkujemy sześciennie itd. Pamiętaj jednak, że zawsze musimy brać pod uwagę założenia dotyczące podstawy logarytmu, o których powiem za chwilę.

Obliczanie podstawy logarytmu: praktyczne przykłady krok po kroku

Teoria jest ważna, ale nic tak nie utrwala wiedzy, jak praktyka. Przygotowałem kilka przykładów, które krok po kroku pokażą Ci, jak zastosować poznane zasady do obliczania podstawy logarytmu. Zobaczysz, że to naprawdę proste!

Przykład 1: klasyczne zadanie z liczbami całkowitymi (logₐ4 = 2)

Rozwiążmy równanie logₐ4 = 2.

1. Przekształcamy na formę potęgową: Zgodnie z definicją, logₐ4 = 2 oznacza a² = 4.
2. Rozwiązujemy równanie potęgowe: Aby znaleźć 'a', pierwiastkujemy obie strony: √a² = √4. Otrzymujemy a = 2 lub a = -2.
3. Sprawdzamy założenia: Pamiętamy, że podstawa logarytmu 'a' musi być dodatnia (a > 0). Dlatego odrzucamy rozwiązanie a = -2.
4. Wynik: Jedynym poprawnym rozwiązaniem jest a = 2.

Przykład 2: co zrobić, gdy wynik logarytmu jest ułamkiem? (logₐ8 = 1/2)

Rozwiążmy równanie logₐ8 = 1/2.

1. Przekształcamy na formę potęgową: logₐ8 = 1/2 oznacza a^(1/2) = 8.
2. Upraszczamy wykładnik ułamkowy: Wiemy, że a^(1/2) to to samo co √a. Zatem mamy √a = 8.
3. Rozwiązujemy równanie: Aby pozbyć się pierwiastka, podnosimy obie strony do kwadratu: (√a)² = 8². Otrzymujemy a = 64.
4. Sprawdzamy założenia: a = 64 jest dodatnie i różne od 1, więc spełnia warunki.
5. Wynik: Rozwiązaniem jest a = 64.

Przykład 3: wyzwanie z ujemnym wynikiem (logₐ(1/9) = -2)

Rozwiążmy równanie logₐ(1/9) = -2.

1. Przekształcamy na formę potęgową: logₐ(1/9) = -2 oznacza a⁻² = 1/9.
2. Upraszczamy wykładnik ujemny: Pamiętamy, że a⁻² to to samo co 1/a². Zatem mamy 1/a² = 1/9.
3. Rozwiązujemy równanie: Z równości ułamków wynika, że a² = 9. Pierwiastkujemy obie strony: √a² = √9. Otrzymujemy a = 3 lub a = -3.
4. Sprawdzamy założenia: Odrzucamy a = -3, ponieważ podstawa musi być dodatnia.
5. Wynik: Rozwiązaniem jest a = 3.

Przykład 4: jak poradzić sobie z potęgami wyższych stopni? (logₐ81 = 4)

Rozwiążmy równanie logₐ81 = 4.

1. Przekształcamy na formę potęgową: logₐ81 = 4 oznacza a⁴ = 81.
2. Rozwiązujemy równanie potęgowe: Aby znaleźć 'a', musimy znaleźć pierwiastek czwartego stopnia z 81. Możemy to zapisać jako a = ⁴√81.
3. Obliczamy pierwiastek: Szukamy liczby, która podniesiona do potęgi czwartej da 81. Wiemy, że 3 * 3 * 3 * 3 = 81. Zatem a = 3 lub a = -3.
4. Sprawdzamy założenia: Odrzucamy a = -3, ponieważ podstawa musi być dodatnia.
5. Wynik: Rozwiązaniem jest a = 3.

Unikaj błędów: najczęstsze pułapki przy obliczaniu podstawy

Nawet doświadczonym osobom zdarzają się pomyłki, zwłaszcza gdy w grę wchodzą dodatkowe warunki. Chciałbym zwrócić Twoją uwagę na najczęstsze pułapki, które mogą pojawić się podczas obliczania podstawy logarytmu. Ich świadomość pomoże Ci ich unikać i zawsze dochodzić do poprawnego rozwiązania.

Zasada nr 1: założenia, o których nie możesz zapomnieć (a > 0 i a ≠ 1)

To absolutnie kluczowy punkt. Logarytm nie jest zdefiniowany dla każdej możliwej podstawy. Aby logarytm miał sens matematyczny w dziedzinie liczb rzeczywistych, podstawa 'a' musi spełniać dwa bardzo ważne warunki:

• Podstawa logarytmu 'a' musi być liczbą dodatnią (a > 0).
• Podstawa logarytmu 'a' musi być różna od 1 (a ≠ 1).

Często, rozwiązując równanie potęgowe, uzyskujemy dwa rozwiązania (np. a = 2 i a = -2). Zawsze musisz sprawdzić, czy uzyskane rozwiązania spełniają te założenia. Zapomnienie o nich to jeden z najczęstszych błędów, prowadzący do akceptowania błędnych wyników.

Błąd, który zdarza się każdemu: mylenie potęg ujemnych i ułamkowych

Innym częstym źródłem błędów jest nieprawidłowe operowanie na potęgach o wykładnikach ujemnych lub ułamkowych. Pamiętaj o tych podstawowych zasadach:

• Potęga o wykładniku ujemnym: a⁻ⁿ = 1/aⁿ (np. 2⁻³ = 1/2³ = 1/8).
• Potęga o wykładniku ułamkowym: a^(m/n) = ⁿ√aᵐ (np. 8^(1/3) = ³√8 = 2).

Precyzyjne stosowanie tych wzorów jest niezbędne do poprawnego rozwiązania równania potęgowego po przekształceniu logarytmu.

Kiedy logarytm ma sens? Warunki istnienia podstawy

Kontynuując temat założeń, warto jeszcze raz podkreślić, że nie każde równanie logarytmiczne da się rozwiązać w dziedzinie liczb rzeczywistych. Zrozumienie, kiedy logarytm jest poprawnie zdefiniowany, jest równie ważne, jak umiejętność jego obliczania.

Dlaczego podstawa nie może być ujemna ani równa 1?

Powody, dla których podstawa logarytmu musi być dodatnia i różna od 1, są czysto matematyczne i logiczne.

Gdyby podstawa była ujemna, na przykład -2, to logarytm z liczby dodatniej mógłby nie istnieć (np. log₋₂8 do jakiej potęgi podnieść -2, żeby otrzymać 8? Do 3. A co z log₋₂4? Do 2. Ale co z log₋₂(-8)? To już się komplikuje, a chcemy, żeby logarytm był jednoznaczny). Co więcej, potęgi o wykładnikach ułamkowych z ujemnej podstawy często nie są liczbami rzeczywistymi. Aby uniknąć tych problemów, matematycy ograniczyli podstawę do liczb dodatnich.

Gdyby podstawa była równa 1, równanie 1ᶜ = b oznaczałoby, że b zawsze musiałoby być równe 1 (bo 1 podniesione do dowolnej potęgi zawsze daje 1). Wtedy logarytm byłby zdefiniowany tylko dla b=1, a jego wartość mogłaby być dowolna (1 do potęgi 5 to 1, 1 do potęgi 10 to 1). Taka sytuacja nie byłaby użyteczna, dlatego wykluczamy podstawę równą 1.

Kiedy zadanie z logarytmem nie ma rozwiązania?

Oprócz warunków dotyczących podstawy 'a', musimy pamiętać także o liczbie logarytmowanej 'b'. Liczba logarytmowana 'b' również musi być liczbą dodatnią (b > 0). Jeśli w zadaniu pojawi się logarytm z liczby ujemnej lub zera (np. log₅(-25) lub log₅0), to takie równanie nie ma rozwiązania w dziedzinie liczb rzeczywistych. Zawsze sprawdzaj ten warunek, zanim zaczniesz obliczenia.

Przeczytaj również: Jak rozwiązać równanie? Poznaj metody i uniknij pułapek!

Trzy kroki do sukcesu: podsumowanie obliczania podstawy logarytmu

Podsumowując, obliczanie podstawy logarytmu to proces, który można sprowadzić do trzech kluczowych kroków. Jeśli będziesz się ich trzymać, z pewnością osiągniesz sukces w każdym zadaniu:

1. Przekształć równanie logarytmiczne na potęgowe: Pamiętaj o fundamentalnej definicji logₐb = c ⇔ aᶜ = b. To jest Twój pierwszy i najważniejszy krok.
2. Rozwiąż równanie potęgowe aᶜ = b dla 'a': Zazwyczaj sprowadza się to do podniesienia obu stron do potęgi 1/c (czyli pierwiastkowania).
3. Sprawdź, czy rozwiązanie spełnia założenia: Upewnij się, że Twoje znalezione 'a' jest dodatnie (a > 0) i różne od 1 (a ≠ 1). Nie zapomnij też, że liczba logarytmowana 'b' musi być dodatnia.