Potęgi w matematyce: Opanuj zasady i unikaj typowych błędów

Potęgowanie to jedna z tych fundamentalnych operacji w matematyce, która na pierwszy rzut oka może wydawać się skomplikowana, ale w rzeczywistości jest genialnym skrótem. Zrozumienie potęg jest absolutnie kluczowe nie tylko do rozwiązywania zadań w szkole, ale także do ogarnięcia wielu zjawisk w nauce, technologii, a nawet finansach. Jako Alan Szymczak, chcę Wam pokazać, że potęgi to nic strasznego, a ich opanowanie otworzy przed Wami drzwi do bardziej zaawansowanych obliczeń i lepszego rozumienia otaczającego nas świata.

Potęgi fundament matematyki, który musisz zrozumieć

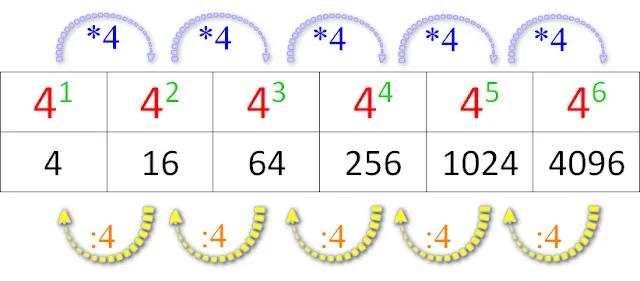
Kiedy zaczynamy przygodę z matematyką, najpierw uczymy się dodawania, potem odejmowania, mnożenia i dzielenia. Potęgowanie to kolejny, naturalny krok w tej ewolucji. To nic innego jak skrócony i bardzo efektywny sposób zapisu wielokrotnego mnożenia tej samej liczby przez siebie. Zamiast pisać 2 * 2 * 2 * 2 * 2, możemy to zapisać znacznie krócej i czytelniej jako 2^5. Ta z pozoru prosta koncepcja staje się fundamentem dla wielu zaawansowanych działów matematyki, fizyki, informatyki i inżynierii. Bez zrozumienia potęg trudno byłoby mi wyobrazić sobie opisywanie zjawisk takich jak wzrost populacji, rozpad promieniotwórczy czy odległości między galaktykami.

Czym tak naprawdę jest potęgowanie? Od mnożenia do potęgi w 3 prostych krokach

Jak już wspomniałem, potęgowanie to nic innego jak uproszczony zapis powtarzającego się mnożenia. Weźmy na przykład liczbę 2 podniesioną do potęgi 3, co zapisujemy jako 2^3. Co to oznacza?

To po prostu 2 pomnożone przez siebie 3 razy:

• Krok 1: Mamy liczbę 2.
• Krok 2: Mnożymy ją przez siebie: 2 * 2 = 4.
• Krok 3: Wynik ponownie mnożymy przez 2: 4 * 2 = 8.

Zatem 2^3 = 8. Widzicie, to naprawdę proste! Liczba, którą potęgujemy, to nasz czynnik, a wykładnik mówi nam, ile razy ten czynnik ma być użyty w mnożeniu. To naprawdę upraszcza zapis i obliczenia, zwłaszcza gdy mamy do czynienia z bardzo dużymi lub bardzo małymi liczbami.

Podstawa i wykładnik poznaj kluczowych graczy w świecie potęg

W każdym wyrażeniu potęgowym, takim jak a^n, mamy do czynienia z dwoma kluczowymi elementami, które musimy dobrze zrozumieć:

• Podstawa potęgi (a): To liczba, którą mnożymy przez siebie. W przykładzie 2^3, liczba 2 jest podstawą. Może to być dowolna liczba rzeczywista dodatnia, ujemna, ułamek, a nawet zero.
• Wykładnik potęgi (n): To mała liczba zapisana w indeksie górnym, która mówi nam, ile razy podstawa ma być pomnożona przez siebie. W przykładzie 2^3, liczba 3 jest wykładnikiem. Wykładnik może być liczbą naturalną, całkowitą (dodatnią lub ujemną), a nawet wymierną (ułamkową), co omówię później.

Zatem, gdy widzicie na przykład 5^4, od razu wiecie, że podstawą jest 5, a wykładnikiem 4, co oznacza 5 * 5 * 5 * 5. Proste, prawda?

Kluczowe prawa działań na potęgach twoja nowa supermoc w liczeniu

Zrozumienie podstawy i wykładnika to dopiero początek. Prawdziwa moc potęg ujawnia się, gdy zaczynamy poznawać zasady, które pozwalają nam na upraszczanie skomplikowanych wyrażeń. Te prawa to jak matematyczne skróty, które oszczędzają nam mnóstwo czasu i wysiłku. Dla mnie to jedne z najbardziej eleganckich i użytecznych narzędzi w matematyce. Przyjrzyjmy się im bliżej.

Jak mnożyć i dzielić potęgi o tych samych podstawach? (Spoiler: to łatwiejsze niż myślisz)

Kiedy mamy do czynienia z potęgami, które mają tę samą podstawę, a chcemy je pomnożyć lub podzielić, zasady są zaskakująco proste. Wystarczy zapamiętać, że przy mnożeniu dodajemy wykładniki, a przy dzieleniu je odejmujemy.

Mnożenie potęg o tych samych podstawach:

Jeśli mamy a^m * a^n, to wynik to a^(m+n). Zobaczmy to na przykładzie:

• 2^3 * 2^2 = (2 * 2 * 2) * (2 * 2) = 2 * 2 * 2 * 2 * 2 = 2^5.
• Zgodnie ze wzorem: 2^(3+2) = 2^5. Wynik się zgadza!

Dzielenie potęg o tych samych podstawach:

Jeśli mamy a^m / a^n, to wynik to a^(m-n). Przykład:

• 3^5 / 3^2 = (3 * 3 * 3 * 3 * 3) / (3 * 3) = 3 * 3 * 3 = 3^3.
• Zgodnie ze wzorem: 3^(5-2) = 3^3. I znowu, wszystko się zgadza!

Te zasady są niezwykle przydatne i pozwalają mi na szybkie upraszczanie wyrażeń, które na pierwszy rzut oka wyglądają na skomplikowane.

Wzory na mnożenie i dzielenie potęg o tej samej podstawie:

• Mnożenie: a^m * a^n = a^(m+n)
• Dzielenie: a^m / a^n = a^(m-n)

Potęga potęgi, czyli jak upraszczać wyrażenia do maksimum?

Co zrobić, gdy chcemy podnieść potęgę do kolejnej potęgi? Na przykład (2^3)^2? Tutaj zasada jest również bardzo intuicyjna: wykładniki po prostu się mnoży. Wzór wygląda tak: (a^m)^n = a^(m*n).

Sprawdźmy to na przykładzie:

• (2^3)^2 = (2 * 2 * 2)^2 = (8)^2 = 8 * 8 = 64.
• Zgodnie ze wzorem: 2^(3*2) = 2^6 = 2 * 2 * 2 * 2 * 2 * 2 = 64.

Jak widać, wynik jest ten sam. Ta zasada jest niesamowicie użyteczna przy upraszczaniu długich i złożonych wyrażeń, pozwalając na szybkie sprowadzenie ich do najprostszej formy. W moim doświadczeniu, to jedno z praw, które najczęściej pozwala mi zaoszczędzić czas.

Co zrobić, gdy podstawy są różne, a wykładniki takie same? Zasady dla potęgi iloczynu i ilorazu

Do tej pory zajmowaliśmy się potęgami o tych samych podstawach. Ale co, jeśli mamy różne podstawy, ale ten sam wykładnik? Na szczęście i na to są proste zasady, które pozwalają nam rozdzielać potęgi na czynniki lub je łączyć.

Potęga iloczynu:

Jeśli mamy iloczyn dwóch liczb podniesiony do potęgi, możemy każdą z tych liczb podnieść do tej potęgi osobno, a następnie pomnożyć wyniki: (a * b)^n = a^n * b^n.

Przykład:

• (2 * 3)^2 = 6^2 = 36.
• Zgodnie ze wzorem: 2^2 * 3^2 = 4 * 9 = 36.

Potęga ilorazu:

Podobnie jest z dzieleniem. Jeśli mamy iloraz dwóch liczb podniesiony do potęgi, możemy każdą z tych liczb podnieść do tej potęgi osobno, a następnie podzielić wyniki: (a / b)^n = a^n / b^n.

Przykład:

• (6 / 3)^2 = 2^2 = 4.
• Zgodnie ze wzorem: 6^2 / 3^2 = 36 / 9 = 4.

Te zasady są niezwykle przydatne, gdy musimy uprościć wyrażenia zawierające ułamki lub iloczyny, a także w algebrze, gdzie często manipulujemy zmiennymi.

Te przypadki potęg sprawiają najwięcej problemów rozpracujmy je raz na zawsze!

Chociaż podstawowe zasady potęgowania są dość intuicyjne, istnieją pewne "specjalne" przypadki wykładników, które często wprowadzają zamieszanie. Mówię tu o wykładniku zerowym, ujemnym i wymiernym (ułamkowym). Wiem z doświadczenia, że to właśnie te zagadnienia potrafią sprawić najwięcej kłopotów. Ale spokojnie, rozłożymy je na czynniki pierwsze i wyjaśnimy tak, abyście już nigdy nie mieli z nimi problemów!

Potęga o wykładniku 0: Dlaczego wynik to zawsze 1?

Jedna z najbardziej intrygujących zasad w potęgowaniu mówi, że każda liczba (z wyjątkiem zera) podniesiona do potęgi zerowej jest równa 1. Tak, dobrze czytacie: 5^0 = 1, (-10)^0 = 1, a nawet (1/2)^0 = 1. Dlaczego tak jest?

Możemy to zrozumieć, korzystając z zasady dzielenia potęg o tej samej podstawie:

• Wiemy, że a^m / a^n = a^(m-n).
• Jeśli m = n, to a^m / a^m = a^(m-m) = a^0.
• Ale każda liczba podzielona przez siebie samą (o ile nie jest zerem) daje 1. Zatem a^m / a^m = 1.
• Stąd wynika, że a^0 = 1.

Ważna uwaga: Wyrażenie 0^0 jest symbolem nieoznaczonym i nie jest równe 1. W większości kontekstów matematycznych przyjmuje się, że podstawa musi być różna od zera, aby a^0 = 1 miało sens.

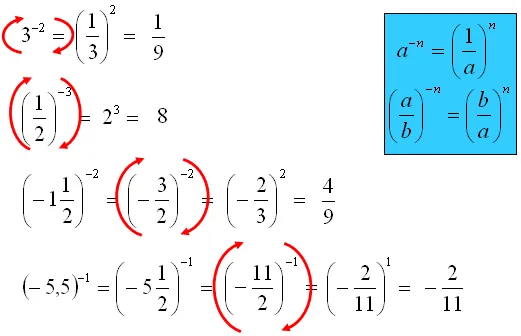
Wykładnik ujemny: Odkryj tajemnicę odwracania liczb

Przykłady:

• 2^(-3) = 1 / 2^3 = 1 / 8.
• 5^(-1) = 1 / 5^1 = 1 / 5.
• (1/3)^(-2) = 1 / (1/3)^2 = 1 / (1/9) = 9.

To pojęcie jest niezwykle ważne, zwłaszcza w notacji naukowej, gdzie używamy potęg liczby 10 z wykładnikami ujemnymi do zapisu bardzo małych liczb, np. masa elektronu czy rozmiar atomu. Dzięki temu możemy pisać liczby takie jak 0.000000001 jako 10^(-9), co jest znacznie wygodniejsze i czytelniejsze.

Co oznacza potęga w ułamku? Związek potęg z pierwiastkami, który musisz znać

Gdy wykładnik potęgi jest ułamkiem (liczbą wymierną), wkraczamy w świat pierwiastków. Potęga o wykładniku wymiernym a^(m/n) jest równoważna n-temu pierwiastkowi z a podniesionego do potęgi m. Czyli a^(m/n) = n-tego stopnia pierwiastek z (a^m).

Najprostszym przykładem jest wykładnik 1/2:

• a^(1/2) = √a (pierwiastek kwadratowy z a).
• Na przykład, 9^(1/2) = √9 = 3.

Inny przykład:

• 8^(2/3) = 3-ciego stopnia pierwiastek z (8^2) = 3-ciego stopnia pierwiastek z (64) = 4.

Zrozumienie tego związku jest kluczowe do rozwiązywania wielu zadań z algebry i pozwala na swobodne przechodzenie między zapisem potęgowym a pierwiastkowym, co jest bardzo przydatne w zaawansowanych obliczeniach.

Najczęstsze pułapki i błędy w potęgowaniu jak ich unikać?

Nawet najbardziej doświadczeni matematycy czasem popełniają błędy, a potęgowanie, mimo swojej prostoty, ma kilka pułapek, w które łatwo wpaść. W mojej pracy widziałem te same pomyłki powtarzane wielokrotnie. Zrozumienie, gdzie te błędy najczęściej się pojawiają, to już połowa sukcesu w ich unikaniu. Przyjrzyjmy się najczęstszym z nich, abyście mogli świadomie je omijać.

Kluczowa różnica między (-a)^n a -a^n: Rola nawiasów w potęgowaniu liczb ujemnych

To jest jeden z najczęstszych błędów, jaki widzę! Różnica między (-a)^n a -a^n jest fundamentalna i często prowadzi do zupełnie innych wyników. Wszystko sprowadza się do roli nawiasów.

• (-a)^n: Kiedy liczba ujemna jest w nawiasie, oznacza to, że cała liczba ujemna jest podstawą potęgi.
• Przykład: (-2)^4 = (-2) * (-2) * (-2) * (-2) = 16 (wynik jest dodatni, bo wykładnik jest parzysty).
• Przykład: (-2)^3 = (-2) * (-2) * (-2) = -8 (wynik jest ujemny, bo wykładnik jest nieparzysty).

• -a^n: Kiedy nie ma nawiasu, to potęgowana jest tylko liczba "a", a znak minus jest traktowany jako mnożenie przez -1 po wykonaniu potęgowania.
• Przykład: -2^4 = -(2 * 2 * 2 * 2) = -16.
• Przykład: -2^3 = -(2 * 2 * 2) = -8.

Jak widać, w przypadku parzystego wykładnika wyniki są diametralnie różne (16 vs -16). Zawsze zwracajcie uwagę na nawiasy to naprawdę ma znaczenie!

Mylenie wzorów kiedy dodajemy, a kiedy mnożymy wykładniki?

Kolejny częsty błąd to mylenie zasad dotyczących wykładników. Pamiętajcie:

• Dodajemy wykładniki, gdy mnożymy potęgi o tej samej podstawie: x^2 * x^3 = x^(2+3) = x^5.
• Mnożymy wykładniki, gdy potęgujemy potęgę: (x^2)^3 = x^(2*3) = x^6.

Bardzo często widzę, jak uczniowie mylą te dwie zasady, np. obliczając (x^2)^3 jako x^5. To błąd! Zawsze zastanówcie się, czy wykonujecie mnożenie potęg, czy potęgowanie potęgi.

Inna pułapka to próba stosowania tych wzorów, gdy podstawy są różne. Na przykład, 2^3 * 3^4 nie równa się (2*3)^(3+4) ani (2*3)^(3*4). W takim przypadku musimy obliczyć każdą potęgę osobno, a następnie pomnożyć wyniki: 2^3 * 3^4 = 8 * 81 = 648.

Błędne skracanie potęg na co uważać przy upraszczaniu ułamków?

Upraszczanie ułamków zawierających potęgi również bywa źródłem błędów. Nigdy nie możemy skracać liczb, które są częścią sumy lub różnicy w liczniku czy mianowniku, jeśli nie możemy wyciągnąć wspólnego czynnika.

Błędne skracanie:

• (a^2 + b^2) / a^2 NIE RÓWNA SIĘ 1 + b^2 (nie możemy skrócić a^2).
• (a^3 - 2) / a NIE RÓWNA SIĘ a^2 - 2 (nie możemy skrócić a).

Poprawne upraszczanie:

• (a^2 + a^3) / a^2 = a^2(1 + a) / a^2 = 1 + a (tutaj możemy skrócić a^2, bo jest wspólnym czynnikiem).
• (6x^5) / (2x^2) = (6/2) * (x^5 / x^2) = 3x^(5-2) = 3x^3.

Zawsze pamiętajcie o kolejności działań i o tym, że skracamy tylko czynniki, a nie składniki sumy czy różnicy!

Czy potęgi przydają się poza szkołą? Zaskakujące zastosowania w świecie realnym

Często słyszę pytanie: "Po co mi to w życiu?". W przypadku potęg odpowiedź jest prosta: są one wszechobecne! Od opisu kosmosu, przez działanie naszych smartfonów, po finanse osobiste. Potęgi to nie tylko abstrakcyjne narzędzie matematyczne, ale praktyczny język, którym posługuje się świat nauki i technologii. Pozwólcie, że pokażę Wam kilka przykładów, które, mam nadzieję, przekonają Was o ich realnej wartości.

Od gwiazd do atomów jak notacja wykładnicza pomaga opisać wszechświat?

Wyobraźcie sobie, że chcecie zapisać odległość Ziemi od Słońca (około 150 000 000 000 metrów) albo masę elektronu (0.000000000000000000000000000000911 kilograma). To byłyby bardzo długie i niewygodne liczby do zapisania i operowania nimi. Tutaj z pomocą przychodzi notacja naukowa (wykładnicza), która wykorzystuje potęgi liczby 10.

• Odległość Ziemi od Słońca: 1.5 * 10^11 metrów.
• Masa elektronu: 9.11 * 10^(-31) kilograma.

Dzięki potęgom możemy w zwięzły i zrozumiały sposób przedstawiać zarówno niewyobrażalnie duże, jak i niewyobrażalnie małe wartości, co jest absolutnie kluczowe w fizyce, astronomii, chemii czy biologii. To dla mnie fascynujące, jak prosta koncepcja potęgowania pozwala nam ogarnąć skalę wszechświata.

Potęgi w Twoim komputerze i smartfonie rola systemu binarnego

Czy zastanawialiście się kiedyś, jak działa Wasz komputer lub smartfon? Cała ich praca opiera się na systemie binarnym, czyli na liczbach 0 i 1. A te 0 i 1 są ściśle związane z potęgami liczby 2. Każdy bit informacji to 0 lub 1. Kiedy łączymy bity, tworzymy bajty, kilobajty, megabajty, gigabajty.

• 1 kilobajt (KB) to 2^10 bajtów = 1024 bajty.
• 1 megabajt (MB) to 2^20 bajtów = 1 048 576 bajtów.
• 1 gigabajt (GB) to 2^30 bajtów = 1 073 741 824 bajty.

Potęgi dwójki są fundamentalne dla informatyki, określając pojemność pamięci, szybkość procesorów i sposób, w jaki dane są przechowywane i przetwarzane. Bez zrozumienia potęg, trudno byłoby mi pojąć, jak działają te wszystkie technologie, z których korzystamy na co dzień.

Przeczytaj również: Opanuj litery greckie w matematyce: Klucz do wzorów!

Jak potęgi pomnażają Twoje pieniądze? Słowo o procencie składanym

Potęgowanie ma również bardzo praktyczne zastosowanie w finansach, a konkretnie w obliczaniu procentu składanego. Jeśli wpłacicie pieniądze na lokatę, która co roku dolicza odsetki nie tylko od początkowej kwoty, ale także od już naliczonych odsetek, to Wasz kapitał rośnie wykładniczo. Wzór na procent składany wygląda następująco:

Kapitał końcowy = Kapitał początkowy * (1 + stopa procentowa)^liczba lat

Jak widać, liczba lat jest wykładnikiem potęgi. Im dłużej pieniądze są inwestowane, tym większy jest efekt potęgowania, a Wasze pieniądze rosną szybciej. To pokazuje, że zrozumienie potęg może pomóc Wam w podejmowaniu lepszych decyzji finansowych i zrozumieniu, jak działają kredyty czy inwestycje. Dla mnie to kolejny dowód na to, że matematyka jest wszędzie!