Wyrażenia algebraiczne: Zrozum fundamenty algebry i unikaj błędów

Wyrażenia algebraiczne to jeden z tych tematów w matematyce, które na początku mogą wydawać się nieco tajemnicze, pełne liter i symboli. Jednak zrozumienie ich budowy i zasad działania jest absolutnie kluczowe, ponieważ stanowią one fundament całej algebry i otwierają drzwi do rozwiązywania problemów w wielu dziedzinach.

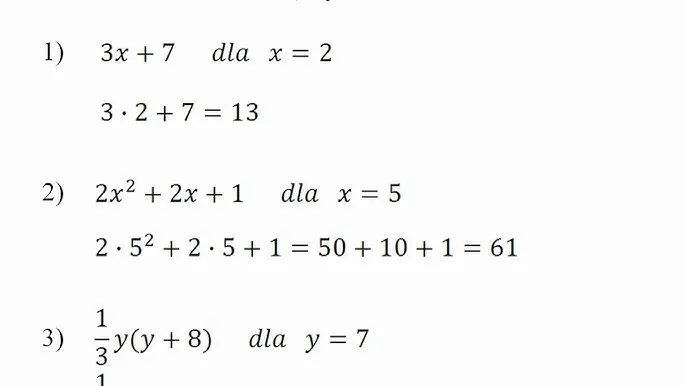
Czym właściwie jest algebra i dlaczego nie trzeba się jej bać?

Zacznijmy od tego, czym właściwie jest algebra. Wyobraź sobie, że idziesz na zakupy. Chcesz kupić kilka jabłek i kilka gruszek. Nie wiesz jeszcze, ile dokładnie sztuk każdego owocu kupisz, ani ile będą kosztować. Algebra pozwala nam opisać taką sytuację za pomocą symboli, zanim poznamy konkretne liczby. Zamiast pisać "koszt jabłek plus koszt gruszek", możemy użyć liter, np. "j" dla jabłek i "g" dla gruszek, i zapisać to jako j + g. To właśnie jest piękno i siła algebry pozwala nam uogólniać i myśleć o relacjach między wielkościami, nawet jeśli nie znamy ich dokładnych wartości.

Wyrażenia algebraiczne to nic innego jak matematyczne zdania, w których obok znanych nam liczb pojawiają się litery. Te litery nazywamy zmiennymi, ponieważ mogą przyjmować różne wartości. Nie ma się czego bać! Traktujmy je jak sprytny sposób na zapisanie pewnej zależności, która może się zmieniać. Na przykład, jeśli chcesz obliczyć obwód kwadratu, możesz użyć wzoru 4 * a, gdzie a to długość boku. Zmienna a może oznaczać 5 cm, 10 cm, a nawet 100 metrów wzór zawsze działa. To sprawia, że matematyka staje się bardziej elastyczna i uniwersalna.

Moim zdaniem, kluczem do oswojenia się z algebrą jest zrozumienie, że litery wcale nie są po to, by komplikować, ale by upraszczać. Pozwalają nam tworzyć uniwersalne reguły i wzory, które działają niezależnie od konkretnych liczb. Kiedy już to zrozumiemy, zobaczymy, że algebra jest bardzo logiczna i intuicyjna.

Anatomia wyrażenia algebraicznego: Poznaj jego części składowe

Aby swobodnie posługiwać się wyrażeniami algebraicznymi, musimy najpierw poznać ich "anatomię", czyli zrozumieć, z jakich elementów się składają. Oto kluczowe pojęcia:

• Zmienna: Litera (np. x, y, a, b), która reprezentuje dowolną liczbę.
  • Przykład: W wyrażeniu 3x + 7, x jest zmienną.
• Współczynnik liczbowy: Liczba stojąca przy zmiennej, przez którą mnożymy tę zmienną.
  • Przykład: W wyrażeniu 3x + 7, 3 jest współczynnikiem liczbowym zmiennej x. Jeśli mamy samo x, to współczynnikiem jest 1 (bo 1x = x).
• Wyraz wolny: Liczba, która nie jest połączona z żadną zmienną.
  • Przykład: W wyrażeniu 3x + 7, 7 jest wyrazem wolnym.
• Jednomian: Najprostsze wyrażenie algebraiczne, będące pojedynczą liczbą, literą lub iloczynem liczb i liter.
  • Przykłady: 5, y, 3ab, -2x².
• Suma algebraiczna: Wyrażenie składające się z jednomianów połączonych znakami plus lub minus.
  • Przykład: 2x - 5y + 8 to suma algebraiczna, składająca się z jednomianów 2x, -5y i 8.

Jak widać, wyrażenie algebraiczne to nic innego jak zbiór tych elementów, połączonych ze sobą w logiczny sposób. Każdy z nich pełni swoją rolę, a ich wspólne działanie pozwala nam opisywać i rozwiązywać różnorodne problemy matematyczne. Zrozumienie tych podstaw to pierwszy krok do swobodnego poruszania się w świecie algebry.

Jak "czytać" i tworzyć własne wyrażenia algebraiczne? Krok po kroku

Przejdźmy teraz do praktyki. Jak zamienić zwykłe zdanie na język matematyki? To trochę jak nauka nowego języka, ale z bardzo prostą gramatyką. Kluczem jest identyfikacja kluczowych słów i przypisanie im odpowiednich symboli.

Załóżmy, że mamy nieznaną liczbę, którą nazwiemy x.

• 'Liczba o 5 większa od x' to po prostu x + 5.
• 'Liczba o 3 mniejsza od x' to x - 3.
• 'Dwukrotność liczby x' (czyli dwa razy więcej) to 2 * x, co zapisujemy jako 2x.
• 'Połowa liczby x' to x / 2 lub 1/2 x.
• 'Suma liczb x i y' to x + y.
• 'Różnica liczb a i b' to a - b.
• 'Iloczyn liczb c i d' to c * d, czyli cd.
• 'Iloraz liczb p i q' to p / q.
• 'Liczba o 7 większa od trzykrotności liczby y' tutaj działamy etapami: trzykrotność liczby y to 3y, a liczba o 7 większa to 3y + 7.

Widzisz? To naprawdę nie jest skomplikowane. Wystarczy krok po kroku analizować zdanie i zamieniać je na symbole. Praktyka czyni mistrza, więc im więcej takich "tłumaczeń" wykonasz, tym szybciej zaczniesz myśleć algebraicznie.

Porządkowanie chaosu, czyli na czym polega redukcja wyrazów podobnych?

Wyrazy podobne to jednomiany, które mają te same zmienne w tych samych potęgach. Na przykład 3x i -5x są wyrazami podobnymi, ponieważ mają tę samą zmienną x w tej samej potędze (do pierwszej). Ale 3x i 3x² nie są podobne, bo x jest w innej potędze. Tak samo 3x i 3y nie są podobne, bo mają różne zmienne.

Jak zatem krok po kroku redukować wyrazy podobne?

1. Zidentyfikuj wyrazy podobne: Przejrzyj całe wyrażenie i znajdź jednomiany, które mają te same zmienne w tych samych potęgach. Dobrą praktyką jest podkreślanie ich różnymi kolorami lub symbolami.
2. Pogrupuj je: Zapisz wyrażenie tak, aby podobne wyrazy znalazły się obok siebie. Pamiętaj o zachowaniu znaków (+/-) stojących przed każdym wyrazem!
3. Dodaj lub odejmij współczynniki liczbowe: Gdy już masz pogrupowane wyrazy podobne, po prostu wykonaj działania (dodawanie lub odejmowanie) na ich współczynnikach liczbowych. Zmienna pozostaje bez zmian.
4. Zapisz uproszczone wyrażenie: Po wykonaniu wszystkich działań otrzymasz uproszczone wyrażenie algebraiczne.

Spójrzmy na kilka przykładów, aby to lepiej zrozumieć:

• 5x + 3x = (5 + 3)x = 8x
• 7y - 2y = (7 - 2)y = 5y
• 4a + 2b - a + 3b = (4a - a) + (2b + 3b) = 3a + 5b
• 6x² + 2x - 3x² + 5x = (6x² - 3x²) + (2x + 5x) = 3x² + 7x (Zauważ, że x² i x to nie są wyrazy podobne!)
• 10 - 3z + 5 + 7z = (-3z + 7z) + (10 + 5) = 4z + 15

Redukcja to nic innego jak porządkowanie. Kiedy już opanujesz tę umiejętność, wiele problemów algebraicznych stanie się znacznie prostszych.

Dlaczego mnożenie i dzielenie wyrażeń jest prostsze, niż myślisz?

Kolejne podstawowe operacje to mnożenie i dzielenie wyrażeń algebraicznych przez liczbę. Tutaj z pomocą przychodzi nam bardzo przydatna zasada, którą nazywamy prawem rozdzielności mnożenia względem dodawania (lub odejmowania). Brzmi skomplikowanie, ale w praktyce jest bardzo intuicyjne. Jeśli masz liczbę przed nawiasem, musisz pomnożyć tę liczbę przez każdy wyraz w nawiasie.

Przykład: 3 * (x + 2)
Tutaj 3 mnożymy przez x ORAZ przez 2.
3 * (x + 2) = 3 * x + 3 * 2 = 3x + 6.
Inny przykład: -2 * (4y - 5)
Pamiętaj o znakach! -2 * (4y - 5) = (-2) * 4y + (-2) * (-5) = -8y + 10.
Jak widzisz, minus razy minus daje plus. To bardzo ważne, aby nie gubić znaków!

Podobnie jest z dzieleniem sum algebraicznych przez liczbę. Dzielenie to tak naprawdę mnożenie przez odwrotność, więc zasada jest podobna: każdy wyraz w sumie algebraicznej dzielimy przez daną liczbę.
Przykład: (6x + 9) / 3
Dzielimy 6x przez 3 ORAZ 9 przez 3.
(6x + 9) / 3 = 6x / 3 + 9 / 3 = 2x + 3.
Inny przykład: (10a - 15b + 5) / (-5)
(10a - 15b + 5) / (-5) = 10a / (-5) - 15b / (-5) + 5 / (-5) = -2a + 3b - 1.
Mimo że na początku może wydawać się to nieco zawiłe, po kilku ćwiczeniach zauważysz, że te operacje są bardzo logiczne i powtarzalne.

Najczęstsze pułapki i błędy sprawdź, czego unikać!

Jako korepetytor, widzę, że pewne błędy powtarzają się u wielu uczniów. Warto je poznać i świadomie unikać, aby szybko opanować algebrę:

• Dodawanie wyrazów, które nie są podobne: To klasyczny błąd. Pamiętaj, że możesz dodawać i odejmować tylko te wyrazy, które mają te same zmienne w tych samych potęgach.
  • Błąd: x + x² = x³ (Nie! Tego nie da się uprościć)
  • Poprawnie: x + x² (zostaje tak jak jest)
  • Błąd: 2a + 3b = 5ab (Nie!)
  • Poprawnie: 2a + 3b (tego również nie da się uprościć)
• Gubienie minusów przy redukcji: Znak minus przed wyrazem należy do tego wyrazu.
  • Błąd: 3x - (-2x) mylone z 3x - 2x. Pamiętaj, że minus i minus daje plus!
    • Błąd: 3x - (-2x) = 3x - 2x = x
    • Poprawnie: 3x - (-2x) = 3x + 2x = 5x
• Zapominanie o mnożeniu każdego wyrazu w nawiasie: To bardzo częsty błąd przy opuszczaniu nawiasów.
  • Błąd: 2 * (x + 3) = 2x + 3 (Zapomniano pomnożyć 3 przez 2)
  • Poprawnie: 2 * (x + 3) = 2x + 2 * 3 = 2x + 6
• Niezrozumienie, że x to to samo co 1x: Czasem brak jawnego współczynnika liczbowego wprowadza w błąd.
  • Błąd: x + 3x = 3x (Zapomniano, że przed x jest 1)
  • Poprawnie: x + 3x = 1x + 3x = 4x

Uważne śledzenie tych pułapek pomoże Ci uniknąć frustracji i szybko nabrać pewności w pracy z wyrażeniami algebraicznymi.

Przeczytaj również: Szacowanie w matematyce: Jak szybko ocenić wyniki i ułatwić życie?

Do czego to wszystko służy? Zobacz algebrę w akcji

Możesz się zastanawiać, po co to wszystko? Czy te x i y przydadzą mi się w życiu? Odpowiedź brzmi: zdecydowanie tak! Wyrażenia algebraiczne to uniwersalny język, który pozwala nam opisywać świat wokół nas w sposób precyzyjny i logiczny. Ich zrozumienie otwiera drzwi do wielu dziedzin.

Zacznijmy od prostych przykładów. Wzory na pole i obwód figur geometrycznych to nic innego jak wyrażenia algebraiczne. Pole prostokąta P = a * b, obwód trójkąta O = a + b + c. Dzięki nim możemy obliczyć potrzebną ilość farby do pomalowania ściany czy długość ogrodzenia działki, niezależnie od jej wymiarów.

W kuchni, jeśli chcesz podwoić przepis na ciasto, musisz pomnożyć ilość każdego składnika przez 2. Jeśli przepis mówi x gramów mąki i y jajek, to potrzebujesz 2x gramów mąki i 2y jajek. To jest właśnie algebra w akcji!

Idąc dalej, wyrażenia algebraiczne są fundamentem fizyki, gdzie opisują zależności między siłą, masą i przyspieszeniem (F = m * a), czy w ekonomii, gdzie pomagają modelować zyski i straty. W informatyce, algorytmy i programowanie opierają się na logicznych wyrażeniach i zmiennych. Nawet w codziennych zagadkach logicznych, gdzie szukamy "pewnej liczby", podświadomie używamy myślenia algebraicznego.

Podsumowując, opanowanie wyrażeń algebraicznych to nie tylko zaliczenie sprawdzianu. To zdobycie narzędzia do logicznego myślenia i rozwiązywania problemów, które spotkasz nie tylko w szkole, ale i w dorosłym życiu. To pierwszy, ale niezwykle ważny krok w fascynującą podróż przez świat matematyki i nauk ścisłych.