Szacowanie w matematyce: Jak szybko ocenić wyniki i ułatwić życie?

Szacowanie w matematyce to niezwykle praktyczna umiejętność, która pozwala nam szybko znaleźć przybliżony wynik działania lub wartości, która jest bliska dokładnemu rezultatowi, ale nie identyczna. To nie tylko szkolna wiedza, ale prawdziwa supermoc na co dzień, ułatwiająca podejmowanie szybkich decyzji, weryfikację wyników i planowanie, zarówno dla uczniów, rodziców, jak i każdego, kto chce sprawniej poruszać się w świecie liczb.

Szacowanie: twoja matematyczna supermoc na co dzień

Czym tak naprawdę jest szacowanie? To więcej niż zgadywanie!

Szacowanie w matematyce to proces, w którym dążymy do znalezienia przybliżonego wyniku działania lub wartości, która jest bliska dokładnemu rezultatowi, ale celowo nie jest z nim identyczna. Moim zdaniem, kluczowe jest zrozumienie, że nie chodzi tu o precyzję, lecz o szybką ocenę rzędu wielkości. To umiejętność, która w polskiej edukacji matematycznej pojawia się zazwyczaj w 4. klasie szkoły podstawowej i stanowi fundament dla bardziej złożonych operacji myślowych.

Po co szacujemy wyniki, skoro mamy kalkulatory?

Często słyszę to pytanie. W dobie wszechobecnych kalkulatorów i smartfonów, szacowanie może wydawać się zbędne. Nic bardziej mylnego! Jako Alan Szymczak, mogę z całą pewnością stwierdzić, że szacowanie to niezastąpione narzędzie. Pozwala nam na szybką weryfikację wyników czy to tych obliczonych w głowie, czy też tych z kalkulatora (tak, kalkulatory też mogą się mylić, a my możemy popełnić błąd przy wprowadzaniu danych!). Ponadto, jest to klucz do efektywnego planowania, na przykład budżetu domowego, podejmowania decyzji bez konieczności sięgania po precyzyjne narzędzia oraz, co najważniejsze, do rozwijania intuicji matematycznej. Dzięki niemu zaczynamy "czuć" liczby.

Szacowanie a dokładny wynik: poznaj kluczowe różnice

Warto jasno rozróżnić szacowanie od dokładnego obliczania. Szacowanie to znacznie szersze pojęcie, które obejmuje myślenie o przybliżonych wartościach. Zaokrąglanie, choć często z nim mylone, jest tak naprawdę tylko jedną z wielu technik szacowania. Wyobraźmy sobie sytuację, gdy ktoś podaje nam wynik mnożenia 28 * 51 jako 14280. Jeśli szybko oszacujemy, że 30 * 50 daje 1500, od razu wiemy, że podana liczba 14280 jest błędna różnica jest zbyt duża, aby mogła być wynikiem szacowania. To właśnie ta zdolność do wychwytywania błędów w rzędzie wielkości czyni szacowanie tak potężnym narzędziem.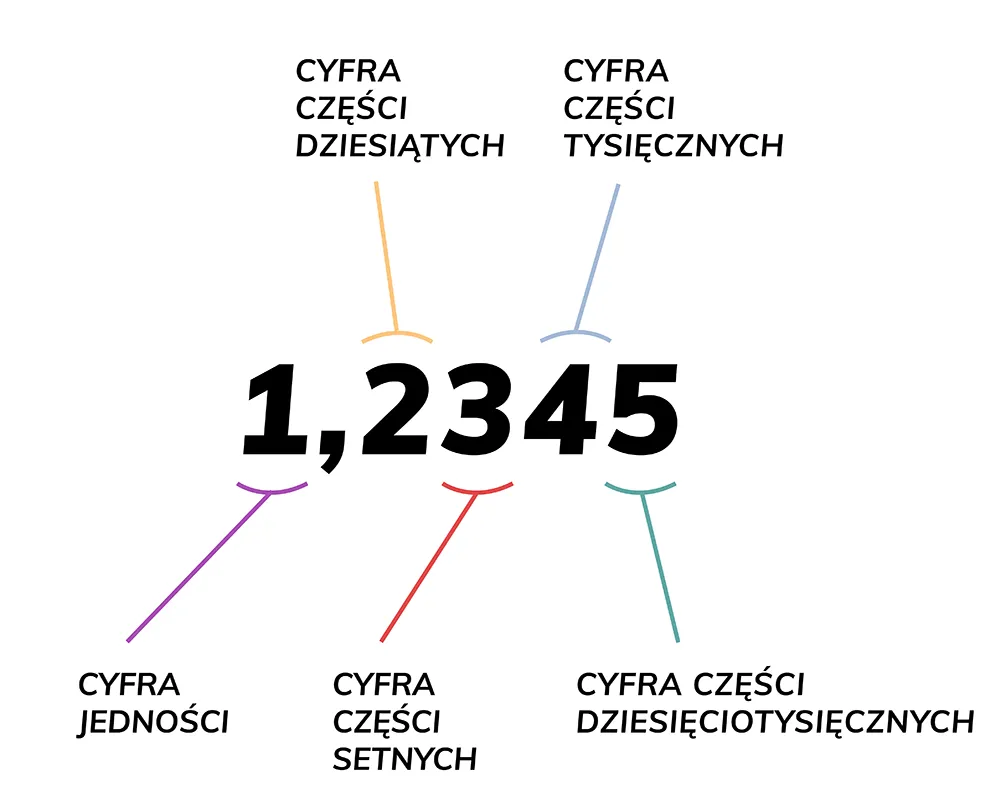

Jak szacować z głową? Poznaj najskuteczniejsze techniki

Technika 1: Zaokrąglanie najprostsza droga do szybkiej odpowiedzi

Zaokrąglanie to bez wątpienia najpopularniejsza i najczęściej stosowana metoda szacowania. Jej prostota polega na tym, że najpierw zaokrąglamy liczby do najbliższej dziesiątki, setki, tysiąca lub innej dogodnej dla nas wartości, a następnie wykonujemy działania na tych zaokrąglonych liczbach. To pozwala na błyskawiczne uzyskanie przybliżonego wyniku. Oto przykład krok po kroku, jak oszacować sumę 487 + 312:

1. Zaokrąglij pierwszą liczbę: 487 zaokrąglamy do najbliższej setki, co daje nam 500.
2. Zaokrąglij drugą liczbę: 312 zaokrąglamy do najbliższej setki, co daje nam 300.
3. Wykonaj działanie na zaokrąglonych liczbach: 500 + 300 = 800.

Oszacowana suma to 800, co jest bardzo bliskie dokładnemu wynikowi 799.

Technika 2: Liczby zgodne twoja tajna broń w mnożeniu i dzieleniu

Metoda liczb zgodnych (nazywanych również kompatybilnymi) to moja ulubiona technika, szczególnie przydatna przy mnożeniu i dzieleniu. Polega ona na zastąpieniu liczb takimi, które są do siebie "zgodne", czyli ułatwiają nam obliczenia w pamięci. Szukamy par, które łatwo się dzielą lub mnożą. Zobaczmy, jak oszacować iloraz 347 / 8:

1. Znajdź liczbę zgodną z dzielnikiem: Zamiast 347, szukamy liczby bliskiej 347, która łatwo dzieli się przez 8. W tym przypadku idealnie pasuje 320 (bo 32 / 8 = 4).
2. Wykonaj działanie na liczbach zgodnych: 320 / 8 = 40.

Oszacowany iloraz to 40. Dokładny wynik to 43.375, więc nasze oszacowanie jest bardzo użyteczne.

Technika 3: Szacowanie od lewej metoda dla zaawansowanych

Szacowanie od lewej do prawej (ang. front-end estimation) to nieco bardziej zaawansowana technika, która skupia się na cyfrach o największej wartości, czyli tych pierwszych od lewej. Jest to szczególnie przydatne, gdy chcemy szybko uzyskać ogólny obraz wyniku. Przykład szacowania sumy 487 + 312 metodą od lewej:

1. Zsumuj cyfry o największej wartości: Patrzymy na setki: 400 + 300 = 700.
2. Opcjonalna korekta: Jeśli chcemy być nieco dokładniejsi, możemy oszacować resztę liczb: 87 + 12 to około 100. Dodając tę korektę do wstępnego oszacowania, otrzymujemy 700 + 100 = 800.

W ten sposób szybko dochodzimy do przybliżonego wyniku 700 lub 800, w zależności od potrzebnej precyzji.

Szacowanie w praktyce: konkretne przykłady

Jak oszacować sumę i różnicę? Sprawdźmy to na rachunku z zakupów

Szacowanie sum i różnic to umiejętność, którą wykorzystujemy niemal codziennie, często nieświadomie. Nic tak nie pomaga w szybkim planowaniu budżetu, jak umiejętność oszacowania, ile zapłacimy za zakupy, zanim jeszcze dotrzemy do kasy.

Przykład 1: Szacowanie sumy (np. 38 zł + 91 zł)

Wyobraź sobie, że masz w portfelu 150 zł i chcesz kupić dwie rzeczy: jedną za 38 zł, drugą za 91 zł. Czy wystarczy Ci pieniędzy?

1. Zaokrąglamy 38 zł do najbliższej dziesiątki: 40 zł.
2. Zaokrąglamy 91 zł do najbliższej dziesiątki: 90 zł.
3. Sumujemy zaokrąglone wartości: 40 zł + 90 zł = 130 zł.

Szybka ocena mówi nam, że 130 zł jest mniej niż 150 zł, więc pieniędzy nam wystarczy. Bez kalkulatora, w kilka sekund!

Przykład 2: Szacowanie różnicy (np. 112 zł - 49 zł)

Kupiłeś coś za 49 zł, płacisz banknotem 112 zł. Ile reszty powinieneś otrzymać?

1. Zaokrąglamy 112 zł do najbliższej dziesiątki: 110 zł.
2. Zaokrąglamy 49 zł do najbliższej dziesiątki: 50 zł.
3. Odejmujemy zaokrąglone wartości: 110 zł - 50 zł = 60 zł.

Możesz spodziewać się około 60 zł reszty. To pomaga szybko sprawdzić, czy sprzedawca nie pomylił się przy wydawaniu.

Jak szybko oszacować iloczyn i iloraz? Koniec z błędami w mnożeniu

Szacowanie iloczynów i ilorazów jest niezastąpione, gdy chcemy szybko zweryfikować wynik lub uniknąć rażących błędów, zwłaszcza w większych obliczeniach.

Przykład 3: Szacowanie iloczynu (np. 28 * 51)

Ktoś twierdzi, że 28 * 51 to 14280. Czy to możliwe?

1. Zaokrąglamy 28 do najbliższej dziesiątki: 30.
2. Zaokrąglamy 51 do najbliższej dziesiątki: 50.
3. Mnożymy zaokrąglone wartości: 30 * 50 = 1500.

Moje oszacowanie wynosi 1500. Wynik 14280 jest dziesięć razy większy! To od razu sygnalizuje, że gdzieś musiał pojawić się błąd (prawdopodobnie ktoś dodał zero na końcu). Szacowanie pomogło nam to wychwycić.

Przykład 4: Szacowanie ilorazu (np. 418 / 8)

Ile mniej więcej wyniesie 418 podzielone przez 8?

1. Szukamy liczby bliskiej 418, która jest łatwo podzielna przez 8. Liczba 400 idealnie pasuje.
2. Dzielimy: 400 / 8 = 50.

Wiem, że wynik będzie około 50. Dokładny wynik to 52.25, więc moje oszacowanie jest bardzo bliskie.

Szacowanie w prawdziwym życiu: zaskakujące zastosowania

Szacowanie na zakupach: czy wystarczy ci pieniędzy do kasy?

To chyba najbardziej oczywiste, ale i najbardziej praktyczne zastosowanie szacowania. Stojąc w kolejce do kasy, mogę szybko oszacować łączny koszt produktów w moim koszyku. Zaokrąglam ceny do pełnych złotówek lub dziesiątek, a następnie sumuję je w głowie. Jeśli mam w portfelu 100 zł, a moje oszacowanie wynosi 95 zł, wiem, że jestem bezpieczny. Jeśli oszacowanie wskazuje na 110 zł, to znak, że muszę odłożyć coś z powrotem na półkę.

Szacowanie w kuchni: jak dostosować przepis dla innej liczby gości?

Jako ktoś, kto lubi gotować, często korzystam ze szacowania w kuchni. Masz przepis na obiad dla 4 osób, a spodziewasz się 6 gości? Musisz zwiększyć proporcje o połowę. Zamiast precyzyjnie przeliczać 150g mąki na 225g, mogę oszacować, że potrzebuję "trochę więcej niż szklankę" lub "półtora raza tyle". To znacznie przyspiesza pracę i pozwala na elastyczność.

Szacowanie w podróży: ile czasu zajmie ci dotarcie do celu?

Planowanie podróży to kolejne pole do popisu dla szacowania. Jeśli wiem, że mam do przejechania 300 km, a średnia prędkość, jaką mogę osiągnąć, to około 80-90 km/h, mogę szybko oszacować, że zajmie mi to około 3,5 do 4 godzin. Podobnie z kosztami paliwa jeśli samochód pali 7 litrów na 100 km, a litr kosztuje 7 zł, to na 300 km wydam około 3 * 7 * 7 = 147 zł. Te szacunki są wystarczające, by zaplanować wyjazd.

Najczęstsze błędy w szacowaniu i jak ich unikać

Błąd 1: Mylenie szacowania z dokładnym obliczaniem

Najczęstszym błędem, jaki widzę, jest próba uzyskania zbyt dużej precyzji w szacowaniu. Pamiętajmy, że szacowanie ma być szybkie i ma dać nam ogólny obraz. Jeśli zaczniemy zaokrąglać do dziesiątych części, a potem do setnych, to tak naprawdę przestajemy szacować, a zaczynamy dążyć do dokładnego wyniku, co niweczy cały cel tej umiejętności.

Błąd 2: Wybieranie nieodpowiedniej metody zaokrąglania

Wybór niewłaściwego rzędu wielkości do zaokrąglania może prowadzić do mało użytecznych oszacowań. Na przykład, jeśli mamy liczby takie jak 487 + 312 i zaokrąglimy je tylko do najbliższej dziesiątki (490 + 310 = 800), to jest to wciąż dobre. Ale gdybyśmy mieli liczby w tysiącach, a zaokrąglali tylko do dziesiątek, wynik mógłby być mylący. Zawsze starajmy się zaokrąglać do rzędu wielkości, który jest sensowny dla danych liczb i celu szacowania.

Błąd 3: Ignorowanie rzędu wielkości wyniku

To błąd, który może mieć poważne konsekwencje. Zawsze po oszacowaniu warto zadać sobie pytanie: "Czy ten wynik ma sens?". Wracając do przykładu 28 * 51, gdzie ktoś podał wynik 14280. Moje oszacowanie (30 * 50 = 1500) od razu pokazało, że wynik jest o rząd wielkości za duży. Ignorowanie tej różnicy mogłoby doprowadzić do zaakceptowania błędnego wyniku. Zawsze sprawdzajmy, czy oszacowany wynik jest w "odpowiedniej lidze".

Przeczytaj również: Wyrażenia algebraiczne: Zrozum fundamenty algebry i unikaj błędów

Dlaczego szacowanie to kluczowa umiejętność?

Jak regularne szacowanie rozwija logiczne myślenie?

Regularne ćwiczenie szacowania to coś więcej niż tylko nauka matematyki. To trening dla naszego mózgu. Rozwija umiejętności analityczne, uczy logicznego myślenia i zdolności do szybkiej oceny sytuacji. Dzięki niemu stajemy się sprawniejsi w podejmowaniu decyzji, nie tylko tych związanych z liczbami. Zaczynamy dostrzegać wzorce, przewidywać i weryfikować, co jest nieocenione w każdej dziedzinie życia.

Podsumowanie: zacznij szacować i ułatw sobie życie

Podsumowując, szacowanie to prawdziwa, praktyczna umiejętność, która ułatwia codzienne życie, sprawia, że matematyka staje się bardziej intuicyjna i mniej zniechęcająca. To nie tylko narzędzie do rozwiązywania zadań, ale sposób myślenia, który pozwala nam czuć się pewniej w świecie liczb. Zachęcam każdego uczniów, rodziców, dorosłych do aktywnego praktykowania szacowania. Zobaczysz, jak szybko stanie się Twoją drugą naturą i jak wiele problemów pomoże Ci rozwiązać bez sięgania po kalkulator.