W świecie matematyki istnieją pewne fundamentalne koncepcje, które potrafią znacząco ułatwić naukę i rozwiązywanie problemów. Jedną z nich są działania odwrotne. W tym artykule, jako Alan Szymczak, pokażę Wam, czym są te operacje, dlaczego ich zrozumienie jest kluczowe dla uczniów, rodziców i nauczycieli, oraz jak wykorzystać je w praktyce do sprawdzania wyników i rozwiązywania równań.
- Działania odwrotne to operacje, które wzajemnie się neutralizują, "cofając" swój efekt i przywracając wartość początkową.
- Podstawowe pary to dodawanie i odejmowanie, mnożenie i dzielenie oraz potęgowanie i pierwiastkowanie.
- Służą do weryfikacji poprawności obliczeń, np. sprawdzania odejmowania za pomocą dodawania.
- Są fundamentalnym narzędziem do rozwiązywania równań z jedną niewiadomą, pozwalając na izolowanie "x".
- Zrozumienie ich buduje głębsze pojmowanie struktury matematyki i zależności między operacjami.
Prosta definicja, która rozjaśni Ci wszystko
Działania odwrotne w matematyce to nic innego jak operacje, które wzajemnie się neutralizują. Wyobraźcie sobie, że wykonujecie jakąś czynność, a potem robicie coś, co sprawia, że wracacie do punktu wyjścia dokładnie tak działają działania odwrotne. One "odwracają" efekt poprzedniej operacji, przywracając wartość początkową. To naprawdę fundamentalne narzędzie, które każdy uczeń powinien opanować.
Dlaczego zrozumienie tej zasady to supermoc w matematyce?
Z mojego doświadczenia wiem, że zrozumienie działań odwrotnych to prawdziwa supermoc w matematyce. Po pierwsze, dają nam niezawodne narzędzie do sprawdzania wyników naszych obliczeń. Ile razy zastanawialiście się, czy dobrze odjęliście? Dzięki działaniom odwrotnym możecie to łatwo zweryfikować. Po drugie, są one absolutnie niezbędne do rozwiązywania równań, zwłaszcza tych z jedną niewiadomą, które są podstawą algebry. Właśnie dzięki nim możemy "izolować" niewiadomą i znaleźć jej wartość. Co więcej, świadomość istnienia tych par pomaga budować głębsze zrozumienie zależności matematycznych i struktury samej matematyki. To pojęcie jest zresztą obecne w podstawie programowej dla szkół podstawowych, co tylko podkreśla jego wagę.

Dodawanie i odejmowanie: Dwa oblicza tej samej monety
Jak odejmowanie "cofa" to, co zrobiło dodawanie? Przykłady, które od razu zrozumiesz
Zacznijmy od najprostszej i najbardziej intuicyjnej pary: dodawania i odejmowania. Te dwie operacje są ze sobą nierozerwalnie związane. Kiedy dodajemy jakąś liczbę, a potem odejmiemy tę samą liczbę, wracamy do punktu wyjścia. Pozwólcie, że pokażę Wam to na przykładzie: jeśli mamy liczbę 5 i dodamy do niej 3, otrzymamy 8 (5 + 3 = 8). Ale jeśli od tej ósemki odejmiemy z powrotem 3, znów otrzymamy 5 (8 - 3 = 5). Widzicie? Odejmowanie dosłownie "cofnęło" efekt dodawania. To jest właśnie esencja działań odwrotnych.
Niezawodna metoda na sprawdzanie wyników: Jak używać dodawania do weryfikacji odejmowania?
Ta zależność jest niezwykle przydatna do sprawdzania poprawności naszych obliczeń, zwłaszcza przy odejmowaniu. Oto jak to zrobić krok po kroku:
- Wykonaj odejmowanie i uzyskaj różnicę.
- Aby sprawdzić wynik, dodaj otrzymaną różnicę do odjemnika (czyli liczby, którą odejmowaliśmy).
- Jeśli wynik tego dodawania jest równy odjemnej (liczbie, od której odejmowaliśmy), to Twoje odejmowanie jest poprawne.
Przykład: Obliczamy 15 - 7 = 8. Aby sprawdzić, dodajemy różnicę (8) do odjemnika (7): 8 + 7 = 15. Ponieważ 15 to nasza odjemna, wiemy, że wynik jest prawidłowy. Proste, prawda?
Praktyczne zadanie: Rozwiązujemy pierwsze równanie z niewiadomą
Działania odwrotne są również kluczem do rozwiązywania równań. Spójrzmy na proste równanie: x + 5 = 10. Naszym celem jest znaleźć wartość 'x'.
- Zauważamy, że do 'x' dodano 5. Działaniem odwrotnym do dodawania jest odejmowanie.
- Aby "pozbyć się" +5 z lewej strony równania, musimy odjąć 5. Ale pamiętajcie o złotej zasadzie równań: co robimy po jednej stronie, musimy zrobić też po drugiej!
- Odejmujemy więc 5 od obu stron równania:
x + 5 - 5 = 10 - 5 - Upraszczamy:
x = 5
W ten sposób, dzięki działaniu odwrotnemu, szybko znaleźliśmy wartość niewiadomej 'x'.
Mnożenie i dzielenie: Odkryj ich nierozerwalną więź
Zobacz, jak dzielenie jest sekretem rozwiązywania zagadek z mnożeniem
Podobnie jak dodawanie i odejmowanie, mnożenie i dzielenie tworzą parę działań odwrotnych. Dzielenie jest operacją, która "cofa" efekt mnożenia. Jeśli pomnożymy jakąś liczbę, a potem podzielimy ją przez ten sam czynnik (oczywiście różny od zera), wrócimy do wartości początkowej. Spójrzmy na przykład: jeśli mamy liczbę 4 i pomnożymy ją przez 2, otrzymamy 8 (4 * 2 = 8). Jeśli teraz tę ósemkę podzielimy przez 2, znów otrzymamy 4 (8 / 2 = 4). Dzielenie idealnie odwróciło operację mnożenia!
Sprawdzanie poprawności dzielenia za pomocą mnożenia krok po kroku
Ta zależność jest niezwykle użyteczna do sprawdzania wyników dzielenia, zwłaszcza gdy mamy do czynienia z większymi liczbami lub dzieleniem z resztą. Oto jak to zrobić:
- Wykonaj dzielenie i uzyskaj iloraz (wynik) oraz ewentualnie resztę.
- Aby sprawdzić wynik, pomnóż otrzymany iloraz przez dzielnik (liczbę, przez którą dzieliliśmy).
- Jeśli wynik tego mnożenia (plus ewentualna reszta) jest równy dzielnej (liczbie, którą dzieliliśmy), to Twoje dzielenie jest poprawne.
Przykład: Obliczamy 18 / 3 = 6. Aby sprawdzić, mnożymy iloraz (6) przez dzielnik (3): 6 * 3 = 18. Ponieważ 18 to nasza dzielna, wynik jest prawidłowy. A co, gdy mamy resztę? 17 / 3 = 5 reszty 2. Sprawdzamy: 5 * 3 + 2 = 15 + 2 = 17. Zgadza się!
Dlaczego znajomość tabliczki mnożenia ułatwia rozumienie działań odwrotnych?
Biegła znajomość tabliczki mnożenia to fundament, który znacząco ułatwia rozumienie i stosowanie działań odwrotnych, zwłaszcza w kontekście dzielenia. Kiedy szybko potrafimy skojarzyć, że 3 razy 6 to 18, automatycznie widzimy, że 18 podzielone przez 3 to 6, a 18 podzielone przez 6 to 3. To buduje intuicję i pozwala na błyskawiczne rozpoznawanie zależności między liczbami, co jest nieocenione zarówno przy sprawdzaniu wyników, jak i przy rozwiązywaniu równań.
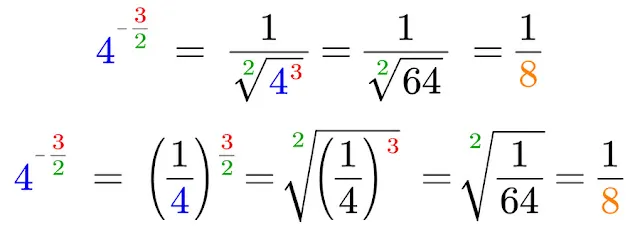
Przenieś swoją wiedzę na wyższy poziom: Potęgowanie i pierwiastkowanie
Czym jest pierwiastkowanie i dlaczego nazywamy je "odwrotnością" potęgowania?
Przejdźmy teraz do nieco bardziej zaawansowanej pary działań odwrotnych: potęgowania i pierwiastkowania. Pierwiastkowanie to działanie, które jest odwrotne do potęgowania. Kiedy podnosimy liczbę do potęgi (np. do kwadratu), a następnie wyciągniemy z wyniku pierwiastek o tym samym stopniu (np. pierwiastek kwadratowy), wracamy do liczby początkowej. Spójrzmy na przykład: jeśli liczbę 3 podniesiemy do kwadratu, otrzymamy 9 (3² = 9). Jeśli teraz z tej dziewiątki wyciągniemy pierwiastek kwadratowy (√9), znów otrzymamy 3. Pierwiastkowanie "cofnęło" potęgowanie. To jest właśnie piękno działań odwrotnych!
Kiedy ta wiedza przydaje się w szkole? Konkretne zadania z potęgami i pierwiastkami
Ta wiedza jest niezwykle przydatna w wielu praktycznych zadaniach, zwłaszcza w geometrii. Wyobraźmy sobie, że mamy kwadrat, którego pole wynosi 25 cm². Pytanie brzmi: jaka jest długość boku tego kwadratu? Wiemy, że pole kwadratu to bok razy bok, czyli bok do kwadratu (a²). Aby znaleźć długość boku (a), musimy wykonać działanie odwrotne do potęgowania, czyli pierwiastkowanie. Zatem a = √25, co daje nam a = 5 cm. Zrozumienie tej zależności pozwala na szybkie i efektywne rozwiązywanie takich problemów.
Jak unikać typowych błędów przy obliczaniu pierwiastków?
Przy obliczaniu pierwiastków, zwłaszcza na początku, łatwo o pomyłki. Oto 2-3 najczęstsze błędy i wskazówki, jak ich unikać:
- Mylenie pierwiastkowania z dzieleniem przez 2: Pamiętajcie, że √9 to nie 9/2. Pierwiastek kwadratowy z 9 to liczba, która pomnożona przez siebie da 9 (czyli 3), a nie jej połowa.
- Brak świadomości, że pierwiastek kwadratowy z liczby ujemnej nie istnieje w zbiorze liczb rzeczywistych: Nie ma takiej liczby rzeczywistej, która pomnożona przez siebie dałaby wynik ujemny. Zawsze sprawdzajcie, czy liczba pod pierwiastkiem jest nieujemna.
- Zapominanie o stopniu pierwiastka: Pierwiastek kwadratowy (stopnia 2) to nie to samo co pierwiastek sześcienny (stopnia 3). Zawsze zwracajcie uwagę na małą liczbę nad znakiem pierwiastka (indeks).
Działania odwrotne w akcji: Jak ułatwiają rozwiązywanie zadań?
Strategia rozwiązywania równań: Krok po kroku do znalezienia "x"
Działania odwrotne są sercem rozwiązywania równań. Moja strategia jest zawsze taka sama: dążymy do tego, aby po jednej stronie równania została tylko niewiadoma 'x', a po drugiej stronie jej wartość. Kluczem jest zawsze wykonywanie tej samej operacji po obu stronach. Spójrzmy na przykład: x - 7 = 12.
- Mamy 'x' i odjęto od niego 7. Działaniem odwrotnym do odejmowania jest dodawanie.
- Aby "pozbyć się" -7 z lewej strony, musimy dodać 7.
- Dodajemy 7 do obu stron równania:
x - 7 + 7 = 12 + 7 - Upraszczamy:
x = 19
Ta prosta, ale potężna strategia pozwala na rozwiązywanie nawet bardziej złożonych równań, krok po kroku "rozplątując" je za pomocą działań odwrotnych.
Jak myślenie o "odwracaniu" pomaga w zadaniach tekstowych?
Zadania tekstowe często sprawiają problemy, ale myślenie o działaniach odwrotnych może je znacząco uprościć. Moim zdaniem, kluczem jest umiejętność przetłumaczenia słów na język matematyki, czyli na równanie. Weźmy przykład: "Miałem 10 zł, dostałem od babci pewną kwotę i mam teraz 25 zł. Ile dostałem od babci?".
Możemy to zapisać jako równanie: 10 + x = 25, gdzie 'x' to kwota, którą dostałem od babci. Aby znaleźć 'x', musimy "odwrócić" dodawanie 10. Wykonujemy działanie odwrotne, czyli odejmujemy 10 od obu stron równania: 10 + x - 10 = 25 - 10. Otrzymujemy x = 15. Dostałem od babci 15 zł. Widzicie, jak działania odwrotne pomagają rozwikłać codzienny problem?
Najczęstsze pułapki i jak ich unikać (np. dzielenie przez zero)
Chociaż działania odwrotne są niezwykle użyteczne, istnieje jedna bardzo ważna pułapka, o której zawsze musimy pamiętać: dzielenie przez zero. Dzielenie przez zero jest matematycznie niedozwolone i nie ma działania odwrotnego. Dlaczego? Ponieważ żadna liczba pomnożona przez zero nie da wyniku różnego od zera. Jeśli mielibyśmy równanie typu 5 * x = 0, to x musiałoby być zerem. Ale jeśli mielibyśmy 5 * x = 10, a chcielibyśmy "odwrócić" mnożenie przez zero, to nie ma takiej liczby, która pomnożona przez 0 dałaby 10. Zawsze upewnijcie się, że nie próbujecie dzielić przez zero w swoich obliczeniach i równaniach!
Podsumowanie: Jak myślenie o działaniach odwrotnych sprawi, że polubisz matematykę?
Krótkie przypomnienie najważniejszych par i ich zastosowań
Podsumowując, działania odwrotne to niezwykle ważny filar matematyki, który ułatwia naukę i rozwiązywanie problemów. Przypomnijmy sobie najważniejsze pary i ich główne zastosowania:
- Dodawanie i odejmowanie: Wzajemnie się neutralizują. Idealne do sprawdzania wyników odejmowania i rozwiązywania równań typu x + a = b.
- Mnożenie i dzielenie: Również wzajemnie się "cofają". Niezastąpione do weryfikacji dzielenia i znajdowania niewiadomej w równaniach typu a * x = b.
- Potęgowanie i pierwiastkowanie: Pierwiastkowanie odwraca potęgowanie. Kluczowe w zadaniach z geometrią (np. pole kwadratu) i rozwiązywaniu równań z potęgami.
Przeczytaj również: Opanuj litery greckie w matematyce: Klucz do wzorów!
Dlaczego to jedno z najważniejszych narzędzi w Twoim matematycznym przyborniku?
Z mojej perspektywy, zrozumienie działań odwrotnych to jedno z najważniejszych narzędzi, jakie możesz mieć w swoim matematycznym przyborniku. Daje Ci pewność siebie, bo wiesz, jak sprawdzić swoje obliczenia. Daje Ci moc rozwiązywania problemów, bo znasz fundamentalną strategię na równania. Co najważniejsze, buduje głębsze, intuicyjne rozumienie matematyki, pokazując, jak operacje są ze sobą powiązane. Gdy tylko opanujesz tę koncepcję, zobaczysz, że matematyka stanie się znacznie bardziej logiczna, a przez to mam nadzieję również bardziej lubiana!

