Pole trójkąta bez wysokości? 3 metody, które musisz znać!

W świecie geometrii, obliczanie pola trójkąta zazwyczaj kojarzy się z prostym wzorem obejmującym podstawę i wysokość. Jednak co zrobić, gdy wysokość jest nieznana lub jej wyznaczenie staje się skomplikowane? Właśnie wtedy z pomocą przychodzą alternatywne metody, które pozwalają skutecznie rozwiązać ten problem. W tym artykule pokażę Ci, jak radzić sobie z takimi wyzwaniami, wykorzystując wzór Herona, trygonometrię i geometrię analityczną.

Gdy brakuje wysokości: Dlaczego klasyczny wzór na pole trójkąta to nie wszystko?

Klasyczny wzór na pole trójkąta, P = 1/2 * a * h, jest fundamentem, którego uczymy się na początku przygody z geometrią. Jest on intuicyjny i prosty, pod warunkiem, że znamy długość podstawy (a) i odpowiadającej jej wysokości (h). Niestety, w wielu zadaniach matematycznych, zwłaszcza tych bardziej złożonych, wysokość nie jest podana wprost, a jej wyznaczenie może być trudniejsze niż znalezienie alternatywnej drogi do rozwiązania. Właśnie w takich momentach okazuje się, że poleganie wyłącznie na tym podstawowym wzorze to za mało.

Poznaj ograniczenia wzoru P = 1/2 * a * h

Z mojego doświadczenia wiem, że podstawowy wzór na pole trójkąta, choć użyteczny, ma swoje ograniczenia. Oto trzy typowe sytuacje, w których staje się on niepraktyczny lub wręcz niemożliwy do zastosowania, zmuszając nas do szukania innych rozwiązań:

• Brak danych o wysokości: Często w zadaniu podane są tylko długości boków trójkąta, a wysokość jest całkowicie nieznana. Próba jej obliczenia może być bardziej skomplikowana niż zastosowanie innego wzoru.
• Wysokość niewymierna lub trudna do wyznaczenia: Nawet jeśli wysokość da się obliczyć, może okazać się, że jest ona liczbą niewymierną, co wprowadza dodatkowe trudności w rachunkach i wymaga zaokrągleń, wpływając na precyzję wyniku.
• Trójkąt w układzie współrzędnych: Gdy wierzchołki trójkąta są podane w układzie współrzędnych, obliczanie wysokości wymagałoby znajomości równania prostej, na której leży podstawa, a następnie odległości punktu (wierzchołka) od tej prostej. To czasochłonne i podatne na błędy.

Jakie dane są kluczowe, by ruszyć z zadaniem bez wysokości?

Zanim wybierzesz odpowiednią metodę, musisz wiedzieć, jakie dane masz do dyspozycji. To absolutna podstawa! Kluczem do sukcesu jest rozpoznanie, który zestaw informacji posiadasz. Możesz mieć podane długości wszystkich trzech boków, co od razu naprowadzi Cię na wzór Herona. Innym razem będziesz dysponować długościami dwóch boków i miarą kąta zawartego między nimi wtedy trygonometria będzie Twoim sprzymierzeńcem. Wreszcie, jeśli trójkąt jest osadzony w układzie współrzędnych, a Ty znasz współrzędne jego wierzchołków, geometria analityczna okaże się niezastąpiona. Pamiętaj, że te zestawy danych są niczym klucze do różnych drzwi każdy otwiera inną, skuteczną ścieżkę do rozwiązania.

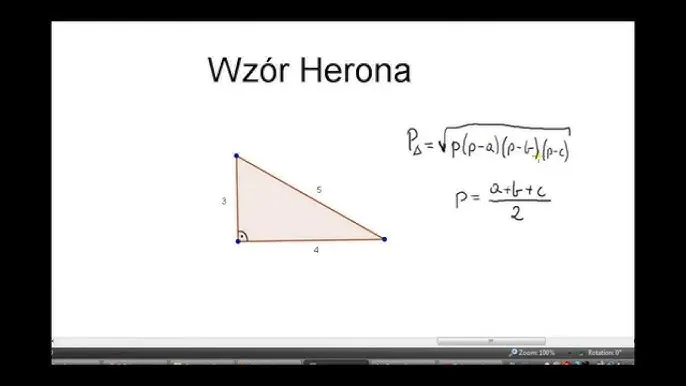
Wzór Herona, czyli siła trzech boków

Wzór Herona to prawdziwy ratunek, gdy dysponujemy jedynie długościami wszystkich trzech boków trójkąta (oznaczmy je jako a, b, c). Jest to eleganckie i potężne narzędzie, które pozwala na obliczenie pola bez konieczności znajdowania wysokości. Sam wzór prezentuje się następująco: P = √[p(p-a)(p-b)(p-c)], gdzie 'p' to połowa obwodu trójkąta.

Kim był Heron i dlaczego jego wzór jest tak genialny?

Heron z Aleksandrii, żyjący w I wieku n.e., był greckim matematykiem i inżynierem. Jego wkład w naukę jest ogromny, a wzór na pole trójkąta, znany dziś jako wzór Herona, to jeden z jego najbardziej znanych osiągnięć. Genialność tego wzoru polega na tym, że umożliwia on obliczenie pola trójkąta, wykorzystując jedynie jego boki. W czasach, gdy pomiary wysokości były często nieprecyzyjne lub trudne do wykonania, wzór Herona stanowił przełom, oferując prostą i niezawodną metodę, która omijała potrzebę znajomości wysokości. To sprawia, że jest on niezwykle użyteczny do dziś, zwłaszcza w kontekście zadań, gdzie wysokość jest nieznana lub jej wyznaczenie jest kłopotliwe.

Krok po kroku: Jak obliczyć połowę obwodu (p)?

Zanim zastosujemy wzór Herona, musimy obliczyć tak zwaną połowę obwodu, którą oznaczamy literą 'p'. To nic innego jak suma długości wszystkich boków trójkąta podzielona przez dwa. Oto jak to zrobić:

1. Zsumuj długości wszystkich boków: Jeśli boki trójkąta mają długości a, b i c, oblicz ich sumę: a + b + c.
2. Podziel sumę przez 2: Wynik sumowania podziel przez 2. Otrzymasz wartość 'p'.
3. Wzór: p = (a + b + c) / 2
4. Przykład: Załóżmy, że trójkąt ma boki o długościach a=3, b=4, c=5.
   • Suma boków: 3 + 4 + 5 = 12
   • Połowa obwodu (p): 12 / 2 = 6
   W tym przypadku p = 6.

Zastosowanie wzoru Herona w praktyce: rozwiązujemy przykładowe zadanie

Przejdźmy do konkretnego przykładu, aby zobaczyć, jak wzór Herona działa w praktyce. Obliczmy pole trójkąta o bokach a=7, b=8, c=9.

1. Oblicz połowę obwodu (p):
   • p = (a + b + c) / 2
   • p = (7 + 8 + 9) / 2
   • p = 24 / 2
   • p = 12
2. Oblicz różnice (p-a), (p-b), (p-c):
   • p - a = 12 - 7 = 5
   • p - b = 12 - 8 = 4
   • p - c = 12 - 9 = 3
3. Podstaw wartości do wzoru Herona:
   • P = √[p(p-a)(p-b)(p-c)]
   • P = √[12 * 5 * 4 * 3]
   • P = √[60 * 12]
   • P = √[720]
4. Uprość pierwiastek (jeśli to możliwe):
   • Aby uprościć √720, szukamy największego kwadratu, który jest jego dzielnikiem. 720 = 144 * 5.
   • P = √(144 * 5)
   • P = √144 * √5
   • P = 12√5

Ostateczne pole trójkąta wynosi 12√5 jednostek kwadratowych.

Najczęstsze błędy przy stosowaniu wzoru Herona i jak ich unikać

Wzór Herona jest potężny, ale jak każde narzędzie, wymaga precyzji. Oto najczęstsze błędy, które widuję u moich uczniów, oraz wskazówki, jak ich unikać:

• Błędy w obliczaniu połowy obwodu (p): Najczęściej zdarza się zapomnieć o podzieleniu sumy boków przez 2. Zawsze dokładnie sprawdzaj ten pierwszy krok!
• Błędy w odejmowaniu w nawiasach: Czasami w pośpiechu odejmujemy 'p' od 'a', zamiast 'a' od 'p'. Pamiętaj, że zawsze odejmujemy długość boku od połowy obwodu: (p-a), (p-b), (p-c).
• Błędy pierwiastkowania: Obliczanie pierwiastka kwadratowego z dużej liczby może być mylące. Jeśli wynik nie jest liczbą całkowitą, staraj się uprościć pierwiastek, wyciągając czynniki przed znak pierwiastka (jak w przykładzie 12√5).
• Pominięcie warunku istnienia trójkąta: Wzór Herona działa tylko dla trójkątów, które faktycznie istnieją. Pamiętaj o zasadzie, że suma długości dwóch dowolnych boków musi być większa od długości trzeciego boku (np. a+b > c). Jeśli ten warunek nie jest spełniony, trójkąt nie istnieje, a wzór Herona zwróci błąd (np. pierwiastek z liczby ujemnej).

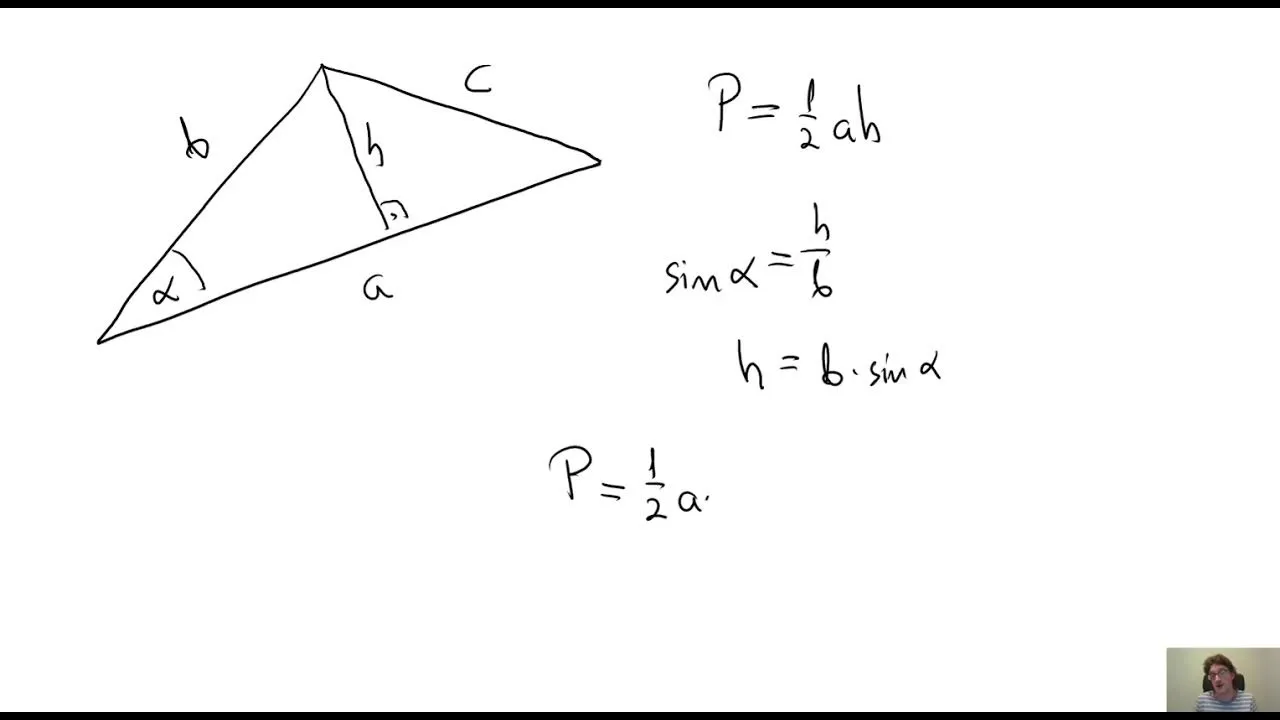
Trygonometria wkracza do gry: pole z dwóch boków i kąta

Kiedy dane są dwa boki trójkąta i kąt zawarty między nimi, trygonometria staje się naszym najlepszym sprzymierzeńcem. To druga, niezwykle użyteczna metoda obliczania pola, która również pozwala ominąć konieczność znajdowania wysokości. Wzór trygonometryczny na pole trójkąta to: P = 1/2 * a * b * sin(γ), gdzie 'a' i 'b' to długości znanych boków, a 'γ' to miara kąta między nimi.

Jak funkcja sinus ratuje sytuację, gdy znasz kąt między bokami?

Funkcja sinus jest kluczowa w tym wzorze, ponieważ pozwala nam w pewnym sensie "stworzyć" wysokość, nawet jeśli nie jest ona podana. Wyobraź sobie trójkąt z bokami 'a' i 'b' oraz kątem 'γ' między nimi. Jeśli z wierzchołka, z którego wychodzą te boki, opuścimy wysokość 'h' na bok 'a' (lub jego przedłużenie), to w powstałym trójkącie prostokątnym funkcja sinus kąta 'γ' będzie równa stosunkowi wysokości 'h' do boku 'b' (sin(γ) = h/b). Stąd możemy wyznaczyć h = b * sin(γ). Podstawiając to do klasycznego wzoru P = 1/2 * a * h, otrzymujemy P = 1/2 * a * b * sin(γ). To elegancki sposób na obejście problemu nieznanej wysokości, wykorzystując relacje kątów i boków w trójkącie.

Kluczowy wzór: P = 1/2 * a * b * sin(γ) jak go rozumieć?

Rozłóżmy ten wzór na czynniki pierwsze, abyś dokładnie wiedział, co oznacza każdy element:

• P: Oczywiście, to pole trójkąta, które chcemy obliczyć.
• 1/2: Stały współczynnik, który pojawia się w większości wzorów na pole trójkąta.
• a i b: To długości dwóch boków trójkąta, które znasz. Ważne jest, aby były to boki, które tworzą kąt γ. Nie mogą to być dowolne dwa boki!
• sin(γ): To wartość funkcji sinus dla kąta γ. Kąt γ to miara kąta zawartego między bokami a i b. Musisz znać ten konkretny kąt, aby wzór zadziałał.

Pamiętaj, że możesz użyć dowolnych dwóch boków i kąta między nimi. Jeśli masz boki 'b' i 'c' oraz kąt 'α' między nimi, wzór będzie wyglądał tak: P = 1/2 * b * c * sin(α). Analogicznie dla boków 'a' i 'c' oraz kąta 'β': P = 1/2 * a * c * sin(β).

Praktyczny przykład: Obliczamy pole trójkąta, znając dwa boki i kąt

Wyobraź sobie trójkąt, w którym znasz długości dwóch boków: a=10 i b=12, a kąt między nimi wynosi 45°. Obliczmy jego pole:

1. Zidentyfikuj dane:
   • a = 10
   • b = 12
   • γ = 45°
2. Znajdź wartość sin(γ):
   • Wartość sin(45°) to √2 / 2, czyli w przybliżeniu 0.7071.
   • Jeśli używasz kalkulatora, upewnij się, że jest ustawiony na stopnie (DEG).
3. Podstaw wartości do wzoru:
   • P = 1/2 * a * b * sin(γ)
   • P = 1/2 * 10 * 12 * sin(45°)
   • P = 1/2 * 120 * (√2 / 2)
   • P = 60 * (√2 / 2)
   • P = 30√2
4. Oblicz wartość przybliżoną (jeśli wymagana):
   • P ≈ 30 * 0.7071
   • P ≈ 21.213

Pole trójkąta wynosi 30√2 jednostek kwadratowych, czyli w przybliżeniu 21.21 jednostek kwadratowych (zaokrąglając do dwóch miejsc po przecinku).

Na co uważać? Tablice wartości trygonometrycznych i użycie kalkulatora

Precyzja w trygonometrii jest kluczowa. Oto kilka rad, na co zwracać uwagę:

• Jednostki miary kąta: To jest absolutnie krytyczne! Upewnij się, że Twój kalkulator jest ustawiony na stopnie (DEG), a nie radiany (RAD) czy grady (GRAD). Błąd w jednostce kąta całkowicie zafałszuje wynik.
• Tablice trygonometryczne: Jeśli korzystasz z tablic, zawsze sprawdzaj, czy odczytujesz wartość dla odpowiedniego kąta i funkcji. Czasem łatwo pomylić sinus z cosinusem.
• Zaokrąglenia: Wartości funkcji trygonometrycznych dla większości kątów nie są liczbami całkowitymi. Staraj się używać jak największej precyzji (więcej miejsc po przecinku) w trakcie obliczeń, a zaokrąglaj dopiero ostateczny wynik do wymaganej liczby miejsc po przecinku.
• Kąty specjalne: Pamiętaj o wartościach funkcji trygonometrycznych dla kątów specjalnych (30°, 45°, 60°, 90°), ponieważ często pojawiają się w zadaniach i ich znajomość przyspiesza obliczenia.

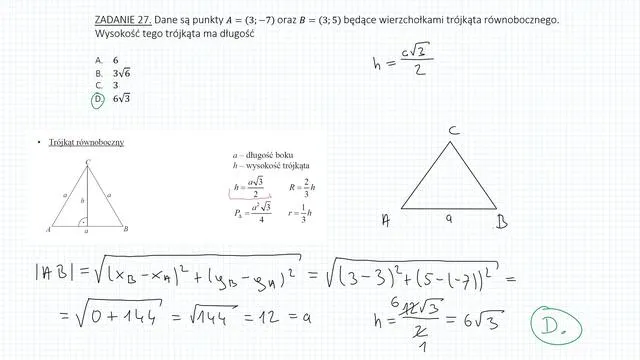
Geometria analityczna, czyli pole ze współrzędnych wierzchołków

Trzecia metoda, którą chcę Ci przedstawić, jest niezwykle przydatna, gdy trójkąt jest "osadzony" w układzie współrzędnych. Jeśli znasz współrzędne wszystkich trzech wierzchołków (A=(x_A, y_A), B=(x_B, y_B), C=(x_C, y_C)), możesz obliczyć jego pole za pomocą wzoru z geometrii analitycznej. Ogólny wzór wygląda następująco: P = 1/2 |(x_B - x_A)(y_C - y_A) - (y_B - y_A)(x_C - x_A)|.

Kiedy ta metoda jest niezastąpiona? Zadania na układzie współrzędnych

Ta metoda jest absolutnie niezastąpiona w zadaniach, gdzie trójkąt jest przedstawiony na płaszczyźnie kartezjańskiej. Zamiast męczyć się z wyznaczaniem wysokości, co w układzie współrzędnych często wymagałoby obliczania równania prostej i odległości punktu od prostej, możemy od razu przejść do obliczeń pola, używając samych współrzędnych. Jest to szczególnie wygodne, gdy wierzchołki mają "ładne" współrzędne, ale działa równie dobrze dla dowolnych punktów. To narzędzie, które każdy uczeń przygotowujący się do matury z matematyki powinien mieć w swoim arsenale.

Tajemniczy wzór z wyznacznikiem odszyfrowujemy krok po kroku

Wzór P = 1/2 |(x_B - x_A)(y_C - y_A) - (y_B - y_A)(x_C - x_A)| może na pierwszy rzut oka wydawać się skomplikowany, ale w rzeczywistości jest bardzo logiczny. Rozłóżmy go:

• 1/2: Standardowy współczynnik.
• |...|: Oznacza wartość bezwzględną. Pole zawsze musi być dodatnie, więc jeśli wynik w nawiasie kwadratowym wyjdzie ujemny, bierzemy jego wartość dodatnią.
• (x_B - x_A) i (y_B - y_A): To różnice współrzędnych, które tworzą wektor AB.
• (x_C - x_A) i (y_C - y_A): To różnice współrzędnych, które tworzą wektor AC.

Wzór ten jest w istocie połową wartości bezwzględnej wyznacznika macierzy utworzonej przez współrzędne wektorów AB i AC. Często nazywa się go również "wzorem sznurowadłowym" lub "metodą wyznacznika", zwłaszcza w nieco innej, bardziej intuicyjnej formie, którą omówię za chwilę.

Przykład z życia wzięty: Oblicz pole trójkąta A=(1, 2), B=(5, 4), C=(3, 7)

Obliczmy pole trójkąta o wierzchołkach A=(1, 2), B=(5, 4), C=(3, 7) za pomocą wzoru analitycznego.

1. Zidentyfikuj współrzędne:
   • x_A = 1, y_A = 2
   • x_B = 5, y_B = 4
   • x_C = 3, y_C = 7
2. Oblicz różnice współrzędnych:
   • x_B - x_A = 5 - 1 = 4
   • y_B - y_A = 4 - 2 = 2
   • x_C - x_A = 3 - 1 = 2
   • y_C - y_A = 7 - 2 = 5
3. Podstaw wartości do wzoru:
   • P = 1/2 |(x_B - x_A)(y_C - y_A) - (y_B - y_A)(x_C - x_A)|
   • P = 1/2 |(4 * 5) - (2 * 2)|
   • P = 1/2 |20 - 4|
   • P = 1/2 |16|
   • P = 1/2 * 16
   • P = 8

Pole trójkąta wynosi 8 jednostek kwadratowych.

Jak nie pomylić się w rachunkach: technika "sznurowadłowa"

Technika "sznurowadłowa" to alternatywny sposób zapisu i obliczania tego samego wzoru, który wielu osobom wydaje się bardziej intuicyjny i mniej podatny na błędy. Polega na uporządkowaniu współrzędnych w kolumnach i "przemnażaniu na krzyż":

1. Zapisz współrzędne wierzchołków jeden pod drugim, powtarzając pierwszy wierzchołek na końcu:

   x_A y_A
   x_B y_B
   x_C y_C
   x_A y_A

2. Pomnóż współrzędne "na skos" w dół w prawo i zsumuj wyniki (np. x_A * y_B, x_B * y_C, x_C * y_A). Otrzymasz S1.
3. Pomnóż współrzędne "na skos" w dół w lewo i zsumuj wyniki (np. y_A * x_B, y_B * x_C, y_C * x_A). Otrzymasz S2.
4. Pole P = 1/2 |S1 - S2|.

Dla przykładu A=(1, 2), B=(5, 4), C=(3, 7):

1 2
5 4
3 7
1 2

• S1 = (1*4) + (5*7) + (3*2) = 4 + 35 + 6 = 45
• S2 = (2*5) + (4*3) + (7*1) = 10 + 12 + 7 = 29
• P = 1/2 |45 - 29| = 1/2 |16| = 8

Ta wizualna metoda pomaga zminimalizować pomyłki w podstawianiu do wzoru.

Którą metodę wybrać? Praktyczny przewodnik decyzyjny

Teraz, kiedy znasz już trzy potężne metody obliczania pola trójkąta bez wysokości, naturalnie pojawia się pytanie: którą wybrać? Odpowiedź jest prosta i zależy wyłącznie od danych, które masz do dyspozycji w zadaniu. Pamiętaj, że każda z tych metod jest najlepsza w konkretnym scenariuszu.

Masz podane 3 boki? Wybór jest tylko jeden!

Jeśli w zadaniu podane są długości wszystkich trzech boków trójkąta (a, b, c), to wzór Herona jest Twoim pierwszym i najlepszym wyborem. Jest on stworzony właśnie do takich sytuacji i pozwala na szybkie i precyzyjne obliczenia bez żadnych dodatkowych kroków.

Dane to 2 boki i kąt? Sięgnij po trygonometrię.

Gdy masz podane długości dwóch boków i miarę kąta zawartego między nimi, to wzór trygonometryczny P = 1/2 * a * b * sin(γ) jest najbardziej odpowiedni. Wykorzystanie funkcji sinus w tym przypadku jest niezwykle efektywne i pozwala na bezpośrednie obliczenie pola.

Zadanie z wierzchołkami w układzie współrzędnych? Geometria analityczna to Twój klucz.

Jeżeli trójkąt jest zdefiniowany przez współrzędne jego wierzchołków w układzie kartezjańskim, metoda z geometrii analitycznej (wzór z wyznacznika/sznurowadłowy) jest niezastąpiona. Unikasz w ten sposób skomplikowanych obliczeń wysokości i odległości, przechodząc od razu do rozwiązania.

Podsumowanie: Twoja nowa matematyczna supermoc

Poznałeś właśnie trzy potężne narzędzia, które pozwolą Ci obliczyć pole trójkąta w sytuacjach, gdy klasyczny wzór z wysokością jest niewystarczający. Wzór Herona, trygonometria i geometria analityczna to nie tylko alternatywy, ale wręcz niezbędne elementy w zestawie umiejętności każdego, kto mierzy się z geometrią. Opanowanie tych metod to prawdziwa matematyczna supermoc!

Dlaczego znajomość tych metod otwiera nowe możliwości?

Opanowanie tych alternatywnych wzorów to znacznie więcej niż tylko nauka kolejnych formułek. To poszerzenie Twoich umiejętności analitycznych i problemowych. Dzięki nim możesz rozwiązywać znacznie bardziej złożone problemy geometryczne, które pojawiają się nie tylko w podręcznikach, ale także na egzaminach, w tym na maturze. Niezależnie od tego, czy stoisz przed zadaniem z brakującą wysokością, kątem czy współrzędnymi, zawsze będziesz miał skuteczne narzędzie do ręki. To daje ogromną pewność siebie i pozwala patrzeć na matematykę z nowej perspektywy.

Przeczytaj również: Jak wyznaczyć równanie prostej? Kompletny poradnik do matury

Jak trenować nowo nabyte umiejętności, by nie zapomnieć wzorów?

Sama znajomość wzorów to dopiero początek. Aby naprawdę je opanować i utrwalić, potrzebujesz regularnej praktyki. Oto moje sprawdzone wskazówki:

• Rozwiązuj zadania z podręczników: Szukaj zadań, które wymagają obliczenia pola trójkąta bez podanej wysokości. Zaczynaj od prostych, a potem przechodź do bardziej skomplikowanych.
• Twórz własne przykłady: Wymyślaj własne trójkąty z różnymi danymi (np. trzy boki, dwa boki i kąt, współrzędne wierzchołków) i próbuj obliczać ich pola. To świetny sposób na zrozumienie, jak działają wzory.
• Regularnie powtarzaj wzory: Zapisuj wzory na kartkach, twórz fiszki. Powtarzaj je co kilka dni, aby utrwalić je w pamięci.
• Korzystaj z zasobów online: W internecie znajdziesz wiele quizów, kalkulatorów i dodatkowych przykładów, które pomogą Ci w ćwiczeniach.
• Tłumacz wzory innym: Jeśli masz kolegę lub koleżankę, która również uczy się matematyki, spróbuj wytłumaczyć jej te metody. Uczenie innych to jedna z najlepszych form utrwalania własnej wiedzy.