Zrozumienie pojęcia czynnika w matematyce to absolutna podstawa dla każdego, kto zaczyna swoją przygodę z arytmetyką, a zwłaszcza z mnożeniem. To klucz do rozłożenia liczb na ich fundamentalne elementy i zrozumienia, jak są one budowane. W tym artykule zabiorę Cię w podróż od podstawowych definicji, poprzez praktyczne przykłady i porównania z innymi działaniami, aż po zaawansowane zastosowania, takie jak rozkład na czynniki pierwsze.
Czynnik w matematyce klucz do zrozumienia mnożenia i budowania liczb
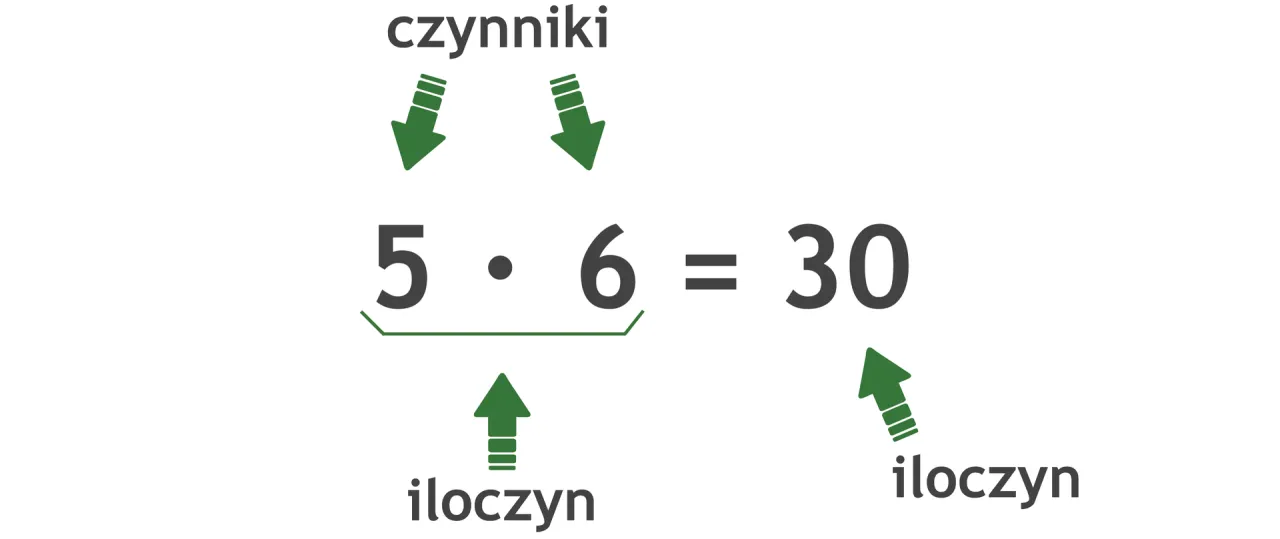
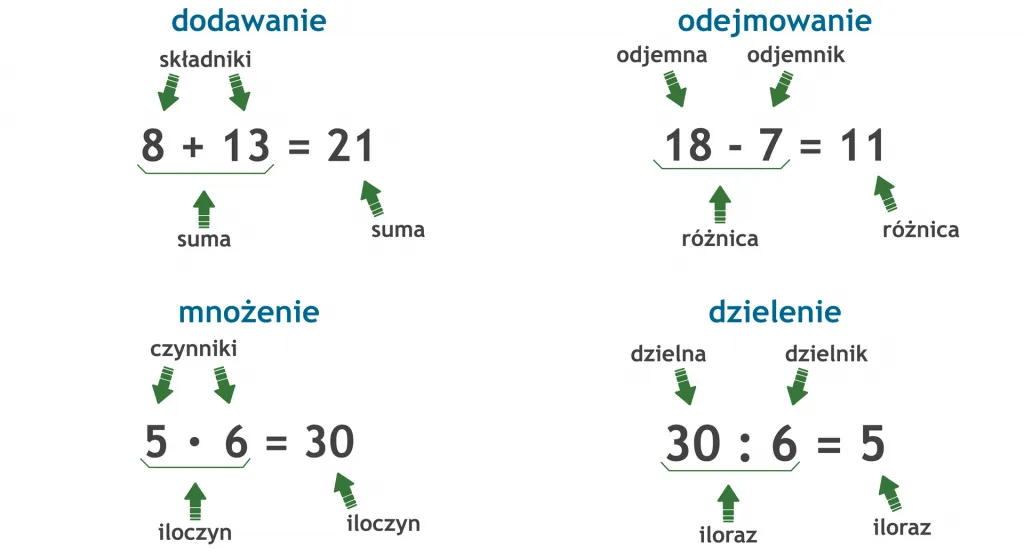
- Czynnik to każda z liczb, które są przez siebie mnożone, a wynik tego działania nazywamy iloczynem (np. w 5 * 4 = 20, liczby 5 i 4 to czynniki).
- Należy odróżniać czynnik (mnożenie) od składnika (dodawanie), aby unikać podstawowych błędów w arytmetyce.
- Czynniki danej liczby to wszystkie liczby naturalne, przez które dzieli się ona bez reszty, czyli jej dzielniki.
- Czynnik pierwszy to szczególny rodzaj czynnika, który jest liczbą pierwszą (ma tylko dwa dzielniki: 1 i samą siebie).
- Rozkład liczby na czynniki pierwsze (faktoryzacja) to przedstawienie jej jako iloczynu wyłącznie liczb pierwszych, co jest podstawą wielu działań matematycznych.
- Znajomość czynników i faktoryzacji ma praktyczne zastosowania, od skracania ułamków po zaawansowaną kryptografię.
Czym jest czynnik? Odkryj klucz do zrozumienia mnożenia
W świecie matematyki, a konkretnie w działaniu mnożenia, czynnik to każda z liczb, które są przez siebie mnożone. Z kolei wynik tego mnożenia nazywamy iloczynem. To naprawdę proste. Weźmy klasyczny przykład: 5 * 4 = 20. W tym działaniu liczby 5 i 4 to czynniki, a liczba 20 to iloczyn. Bez czynników nie byłoby mnożenia, a co za tym idzie iloczynu!
Czynniki odgrywają kluczową rolę w mnożeniu, a ich zrozumienie ułatwia przyswojenie sobie podstawowych własności tego działania:
- Przemienność: Kolejność czynników nie ma znaczenia dla wyniku. Oznacza to, że 3 * 5 da nam ten sam iloczyn co 5 * 3, czyli 15. To bardzo wygodna własność, prawda?
- Łączność: Jeśli mnożymy więcej niż dwie liczby, sposób ich grupowania nie zmienia iloczynu. Na przykład, (2 * 3) * 4 = 6 * 4 = 24, ale także 2 * (3 * 4) = 2 * 12 = 24. Wynik jest ten sam, niezależnie od tego, jak "połączymy" czynniki.
- Element neutralny: Liczba 1 jest specjalnym czynnikiem. Pomnożenie dowolnej liczby przez 1 nie zmienia jej wartości. Czyli 7 * 1 zawsze będzie równe 7.
- Mnożenie przez zero: To kolejna ważna zasada. Jeśli choć jeden z czynników wynosi 0, cały iloczyn zawsze będzie równy 0. Niezależnie od tego, jak duża jest druga liczba, 9 * 0 zawsze da nam 0.
Czynnik to nie składnik! Jak nie mylić pojęć matematycznych?
Często na początku nauki matematyki uczniowie mylą pojęcia czynnika i składnika. Pamiętajmy, że czynnik i iloczyn są nierozerwalnie związane z działaniem mnożenia. Czynniki to elementy, które "składają się" na iloczyn poprzez mnożenie.
Z drugiej strony, w działaniu dodawania mamy do czynienia ze składnikami i sumą. Składniki to liczby, które do siebie dodajemy, a ich wynik to suma. Na przykład, w działaniu 2 + 3 = 5, liczby 2 i 3 to składniki, a liczba 5 to suma.
Aby ułatwić zrozumienie i uniknąć pomyłek, przygotowałem krótkie zestawienie:
| Pojęcie | Opis i przykład |
|---|---|
| Czynnik | Liczba, która jest mnożona przez inną liczbę w celu uzyskania iloczynu. Przykład: W 6 * 2 = 12, liczby 6 i 2 to czynniki. |
| Iloczyn | Wynik działania mnożenia. Przykład: W 6 * 2 = 12, liczba 12 to iloczyn. |
| Składnik | Liczba, która jest dodawana do innej liczby w celu uzyskania sumy. Przykład: W 6 + 2 = 8, liczby 6 i 2 to składniki. |
| Suma | Wynik działania dodawania. Przykład: W 6 + 2 = 8, liczba 8 to suma. |
Kluczowa różnica polega na tym, że czynniki są mnożone, a składniki są dodawane. Mylenie tych pojęć to jeden z najczęstszych błędów na wczesnych etapach nauki, dlatego warto poświęcić chwilę na ich utrwalenie.
Jak znaleźć wszystkie czynniki danej liczby? Prosta instrukcja krok po kroku
Kiedy mówimy o "czynnikach danej liczby", mamy na myśli wszystkie liczby naturalne, przez które ta liczba dzieli się bez reszty. Innymi słowy, są to jej dzielniki. Na przykład, dla liczby 12, jej czynnikami są: 1, 2, 3, 4, 6 i 12. Każda z tych liczb dzieli 12 bez reszty.
Jak znaleźć wszystkie czynniki dla dowolnej liczby? Oto prosta metoda:
- Zacznij od liczby 1. Zawsze jest ona czynnikiem każdej liczby naturalnej.
- Sprawdzaj kolejne liczby naturalne (2, 3, 4, itd.), czy dzielą daną liczbę bez reszty. Jeśli tak, to jest to czynnik.
- Kontynuuj ten proces, aż dojdziesz do liczby, której kwadrat jest większy niż badana liczba. Jeśli znajdziesz czynnik 'a', to 'liczba / a' również będzie czynnikiem.
- Wypisz wszystkie znalezione czynniki.
Zastosujmy tę metodę do kilku przykładów:
-
Dla liczby 18:
- 1 (18 / 1 = 18)
- 2 (18 / 2 = 9)
- 3 (18 / 3 = 6)
- 4 (nie dzieli bez reszty)
- 5 (nie dzieli bez reszty)
- 6 (już znaleziono jako 18/3)
- 9 (już znaleziono jako 18/2)
- 18 (już znaleziono jako 18/1)
Czynniki liczby 18 to: 1, 2, 3, 6, 9, 18.
-
Dla liczby 24:
- 1 (24 / 1 = 24)
- 2 (24 / 2 = 12)
- 3 (24 / 3 = 8)
- 4 (24 / 4 = 6)
- 5 (nie dzieli bez reszty)
- 6 (już znaleziono jako 24/4)
- 8 (już znaleziono jako 24/3)
- 12 (już znaleziono jako 24/2)
- 24 (już znaleziono jako 24/1)
Czynniki liczby 24 to: 1, 2, 3, 4, 6, 8, 12, 24.
-
Dla liczby 30:
- 1 (30 / 1 = 30)
- 2 (30 / 2 = 15)
- 3 (30 / 3 = 10)
- 4 (nie dzieli bez reszty)
- 5 (30 / 5 = 6)
- 6 (już znaleziono jako 30/5)
- 10 (już znaleziono jako 30/3)
- 15 (już znaleziono jako 30/2)
- 30 (już znaleziono jako 30/1)
Czynniki liczby 30 to: 1, 2, 3, 5, 6, 10, 15, 30.
Jak widać, liczby mogą mieć różną liczbę czynników. Liczby pierwsze (o których za chwilę) mają tylko dwa czynniki: 1 i samą siebie. Liczba 1 jest wyjątkiem ma tylko jeden czynnik (samą siebie). Ciekawe są też liczby będące kwadratami (np. 4, 9, 16), które zawsze mają nieparzystą liczbę czynników. To dlatego, że ich pierwiastek kwadratowy jest czynnikiem, który występuje tylko raz, a nie w parze (np. dla 9 są to 1, 3, 9).
Wprowadzenie do czynników pierwszych fundament arytmetyki
Przechodząc do bardziej zaawansowanych, ale równie fundamentalnych koncepcji, musimy zdefiniować liczbę pierwszą. Jest to liczba naturalna większa od 1, która ma dokładnie dwa dzielniki: 1 i samą siebie. To bardzo ważna definicja. Przykłady liczb pierwszych to 2, 3, 5, 7, 11, 13 i tak dalej. Pamiętaj, że 1 nie jest liczbą pierwszą, ponieważ ma tylko jeden dzielnik.
Mając tę definicję, możemy teraz zrozumieć, czym jest czynnik pierwszy. To po prostu czynnik danej liczby, który jest jednocześnie liczbą pierwszą. Różnica między "zwykłym" czynnikiem a czynnikiem pierwszym jest taka, że czynnik może być liczbą złożoną (czyli taką, która ma więcej niż dwa dzielniki, np. 4, 6, 8), natomiast czynnik pierwszy musi być zawsze liczbą pierwszą. Na przykład, dla liczby 12, czynniki to 1, 2, 3, 4, 6, 12. Ale jej czynniki pierwsze to tylko 2 i 3.
Pojęcie czynników pierwszych jest tak ważne, że stanowi podstawę Fundamentalnego Twierdzenia Arytmetyki. Mówi ono, że każdą liczbę złożoną naturalną większą od 1 można jednoznacznie przedstawić w postaci iloczynu czynników pierwszych (pomijając kolejność tych czynników). To twierdzenie jest niczym DNA liczb każda liczba ma swoją unikalną "recepturę" złożoną z liczb pierwszych. To naprawdę fascynujące!

Rozkład na czynniki pierwsze, czyli jak rozebrać liczbę na części
Proces przedstawiania liczby złożonej w postaci iloczynu wyłącznie liczb pierwszych nazywamy rozkładem na czynniki pierwsze, lub fachowo faktoryzacją. Jest to jedna z najważniejszych umiejętności w matematyce, ponieważ pozwala nam "rozebrać" liczbę na jej najprostsze, niepodzielne elementy. Ma to ogromne znaczenie, chociażby przy znajdowaniu Największego Wspólnego Dzielnika (NWD) czy Najmniejszej Wspólnej Wielokrotności (NWW), o czym opowiem za chwilę.
Najprostszą i najpopularniejszą metodą rozkładu na czynniki pierwsze jest metoda "pionowej kreski". Oto jak to działa krok po kroku:
- Zapisz liczbę, którą chcesz rozłożyć, a obok niej narysuj pionową kreskę.
- Zacznij dzielić liczbę przez najmniejszą możliwą liczbę pierwszą (zazwyczaj 2).
- Jeśli dzielenie jest bez reszty, zapisz wynik pod dzieloną liczbą, a czynnik pierwszy (przez który dzieliłeś) po prawej stronie kreski.
- Powtarzaj krok 2 i 3 z nowo uzyskanym wynikiem, zawsze dzieląc przez najmniejszą możliwą liczbę pierwszą.
- Kontynuuj, aż uzyskasz 1 jako wynik dzielenia.
- Wszystkie liczby po prawej stronie kreski to czynniki pierwsze danej liczby.
Zobaczmy to na przykładach:
-
Rozkład liczby 72 na czynniki pierwsze:
72 | 2 36 | 2 18 | 2 9 | 3 3 | 3 1 |
Zatem 72 = 2 * 2 * 2 * 3 * 3
-
Rozkład liczby 100 na czynniki pierwsze:
100 | 2 50 | 2 25 | 5 5 | 5 1 |
Zatem 100 = 2 * 2 * 5 * 5
-
Rozkład liczby 150 na czynniki pierwsze:
150 | 2 75 | 3 25 | 5 5 | 5 1 |
Zatem 150 = 2 * 3 * 5 * 5
Gdzie w praktyce przydaje się znajomość czynników?
Znajomość czynników, a zwłaszcza czynników pierwszych i umiejętność rozkładu liczb, ma ogromne znaczenie w wielu obszarach matematyki i nie tylko. W szkolnej matematyce jest to narzędzie niezbędne do:
- Skracania ułamków: Aby skrócić ułamek, musimy znaleźć wspólne czynniki w liczniku i mianowniku i je "wyeliminować". Na przykład, aby skrócić ułamek 12/18, rozkładamy 12 = 2 * 2 * 3 i 18 = 2 * 3 * 3. Wspólne czynniki to 2 i 3. Skracając je, otrzymujemy 2/3.
- Znajdowania Największego Wspólnego Dzielnika (NWD): NWD to największa liczba, przez którą dzielą się bez reszty dwie lub więcej liczb. Aby go znaleźć, rozkładamy liczby na czynniki pierwsze i mnożymy przez siebie wszystkie wspólne czynniki. Dla 12 i 18, NWD(12, 18) = 2 * 3 = 6.
- Znajdowania Najmniejszej Wspólnej Wielokrotności (NWW): NWW to najmniejsza liczba, która jest wielokrotnością dwóch lub więcej liczb. Aby ją znaleźć, rozkładamy liczby na czynniki pierwsze, a następnie mnożymy przez siebie wszystkie czynniki, biorąc pod uwagę ich największą potęgę. Dla 12 i 18, NWW(12, 18) = (2 * 2 * 3) * 3 = 36.
Pojęcie czynnika nie ogranicza się tylko do arytmetyki. W algebrze również spotykamy się z czynnikami, ale w kontekście wyrażeń algebraicznych. Na przykład, w wyrażeniu 3x(y+1), liczby 3, x i wyrażenie (y+1) są czynnikami. Rozkładanie wielomianów na czynniki, czyli przedstawianie ich w postaci iloczynu prostszych wyrażeń, jest kluczową umiejętnością w algebrze, pomagającą w rozwiązywaniu równań i upraszczaniu wyrażeń.
Co więcej, znaczenie czynników wykracza daleko poza salę lekcyjną. Duże liczby pierwsze i ich czynniki są fundamentem kryptografii, czyli nauki o zabezpieczaniu danych. Algorytmy takie jak RSA, które chronią nasze komunikacje w internecie, bankowość elektroniczną i wiele innych cyfrowych interakcji, opierają się na fakcie, że rozłożenie bardzo dużej liczby na jej czynniki pierwsze jest niezwykle trudne i czasochłonne dla komputerów, nawet tych najpotężniejszych. To pokazuje, jak podstawowe pojęcie czynnika, które poznajemy na wczesnym etapie edukacji, staje się kluczowym elementem w zaawansowanych technologiach, wpływając na nasze codzienne bezpieczeństwo w cyfrowym świecie.