Zastanawiasz się, czym jest obwód trójkąta i jak go obliczyć? To jedno z podstawowych zagadnień w matematyce, które każdy uczeń powinien dobrze zrozumieć. Obwód to nic innego jak suma długości wszystkich boków figury, czyli po prostu miara "dookoła" niej. Zrozumienie tych wzorów to klucz do rozwiązywania wielu zadań, nie tylko tych szkolnych, ale i tych, które spotykamy w życiu codziennym.
Obwód trójkąta: Proste wzory i przykłady, które pomogą Ci w zadaniach
- Ogólny wzór na obwód trójkąta to suma długości jego trzech boków: Obw = a + b + c.
- Dla trójkąta równobocznego, gdzie wszystkie boki są równe, wzór upraszcza się do: Obw = 3a.
- W trójkącie równoramiennym z dwoma równymi ramionami (a) i podstawą (b) obwód obliczysz jako: Obw = 2a + b.
- W trójkącie prostokątnym, jeśli brakuje jednego boku, możesz go znaleźć za pomocą twierdzenia Pitagorasa (a² + b² = c²).
- Zawsze upewnij się, że wszystkie długości boków są wyrażone w tych samych jednostkach przed przystąpieniem do obliczeń.
- Pamiętaj o nierówności trójkąta: suma długości dwóch dowolnych boków musi być większa od długości trzeciego boku.
Definicja, którą zrozumiesz w 10 sekund
Kiedy mówimy o obwodzie trójkąta, mamy na myśli po prostu całkowitą długość linii, która tworzy jego granice. Wyobraź sobie, że idziesz wzdłuż krawędzi trójkątnego pola obwód to cała droga, którą musiałbyś pokonać, aby wrócić do punktu wyjścia. To nic innego jak suma długości wszystkich jego boków.
Kluczowy wzór na obwód każdego trójkąta: poznaj i zapamiętaj
Niezależnie od tego, czy trójkąt jest duży, mały, prostokątny czy ostrokątny, zawsze możemy zastosować ten sam, podstawowy wzór. Jeśli oznaczymy długości boków trójkąta jako a, b i c, to jego obwód (Obw) obliczymy w następujący sposób:
Obw = a + b + c
To jest naprawdę proste! Wystarczy zsumować długości wszystkich trzech boków. Ten wzór to absolutna podstawa, którą warto zapamiętać, bo działa w każdym przypadku.
Dlaczego jednostki mają znaczenie? O czym musisz pamiętać przed obliczeniami
Zanim zaczniesz dodawać długości boków, musisz zwrócić uwagę na jedną bardzo ważną rzecz: wszystkie długości muszą być wyrażone w tych samych jednostkach! Nie możesz dodać centymetrów do milimetrów bez wcześniejszego przeliczenia. To tak, jakbyś próbował dodać jabłka do gruszek. Na przykład, jeśli jeden bok ma 10 cm, a drugi 50 mm, musisz najpierw przeliczyć 50 mm na 5 cm (bo 1 cm = 10 mm). Dopiero wtedy możesz je dodać do pozostałych boków. To częsty błąd, na który ja sam zwracałem uwagę moim uczniom pamiętaj o tym, a unikniesz wielu pomyłek!

Obwód trójkąta równobocznego: Błyskawiczny sposób na obliczenia
Wzór, który maksymalnie upraszcza obliczenia
Trójkąt równoboczny to wyjątkowa figura, ponieważ wszystkie jego boki mają identyczną długość. Oznacza to, że jeśli jeden bok ma długość 'a', to pozostałe dwa również mają długość 'a'. Dzięki temu obliczenie obwodu staje się jeszcze prostsze! Zamiast dodawać a + a + a, możemy po prostu pomnożyć długość jednego boku przez 3. Wzór na obwód trójkąta równobocznego to:
Obw = 3a
To naprawdę oszczędza czas!
Przykład krok po kroku: Obliczamy obwód trójkąta równobocznego o boku 5 cm
Przejdźmy do praktyki. Załóżmy, że mamy trójkąt równoboczny, którego każdy bok ma długość 5 cm. Jak obliczyć jego obwód?
- Zidentyfikuj rodzaj trójkąta: To trójkąt równoboczny, więc wszystkie boki są równe.
- Zapisz długość boku: a = 5 cm.
- Zastosuj wzór: Obw = 3a.
- Podstaw wartości i oblicz: Obw = 3 * 5 cm = 15 cm.
Jak widzisz, obwód tego trójkąta wynosi 15 cm. Proste, prawda?
Obwód trójkąta równoramiennego: Co musisz wiedzieć?
Rozpoznawanie ramion i podstawy klucz do poprawnego wzoru
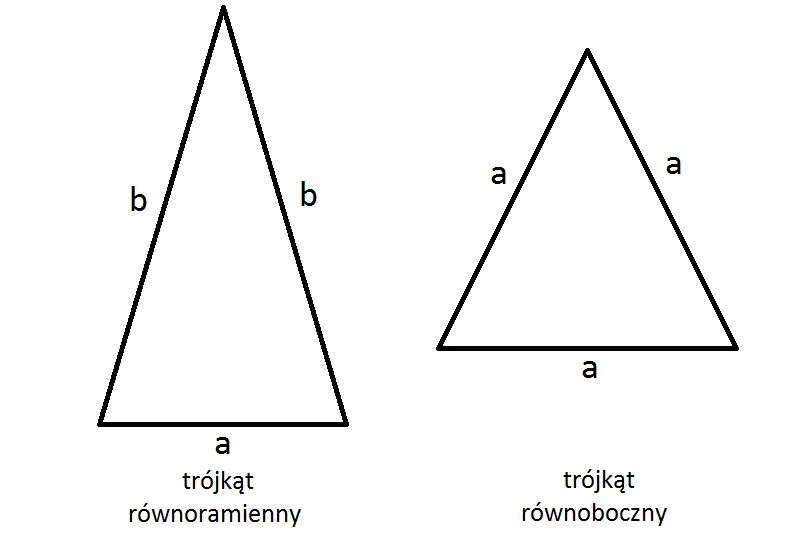
Trójkąt równoramienny to taki, który ma dwa boki równej długości. Te równe boki nazywamy ramionami, a trzeci, różny od nich bok, to podstawa. Kluczem do sukcesu w obliczaniu obwodu takiego trójkąta jest właśnie prawidłowe rozpoznanie, które boki są ramionami, a który jest podstawą. Zawsze upewnij się, że wiesz, które długości są takie same!
Wzór na obwód trójkąta z dwoma takimi samymi bokami
Skoro dwa boki są równe, możemy nieco uprościć ogólny wzór. Jeśli długość ramienia oznaczymy jako 'a', a długość podstawy jako 'b', to wzór na obwód trójkąta równoramiennego będzie wyglądał tak:
Obw = 2a + b
To logiczne, prawda? Dodajemy dwa ramiona i jedną podstawę.
Praktyczne zadanie: Trójkąt o podstawie 6 cm i ramieniu 8 cm
Wyobraź sobie trójkąt równoramienny, w którym podstawa ma 6 cm, a każde z ramion po 8 cm. Jak obliczyć jego obwód?
- Zidentyfikuj długości: Długość ramienia (a) = 8 cm, długość podstawy (b) = 6 cm.
- Zastosuj wzór: Obw = 2a + b.
- Podstaw wartości i oblicz: Obw = (2 * 8 cm) + 6 cm = 16 cm + 6 cm = 22 cm.
Obwód tego trójkąta równoramiennego wynosi 22 cm. Widzisz, to wcale nie jest trudne, jeśli wiesz, co jest czym!

Obwód trójkąta prostokątnego: Jak pokonać wyzwania?
Standardowy wzór, który zawsze działa
Trójkąt prostokątny, choć ma swoją specyficzną cechę (kąt prosty), nadal jest trójkątem! To oznacza, że ogólny wzór na obwód Obw = a + b + c jest w pełni aktualny. Jeśli znasz długości wszystkich trzech boków, po prostu je sumujesz i masz wynik. Nic się nie zmienia w samej metodzie dodawania.
Co zrobić, gdy brakuje jednego boku? Twój przyjaciel Pitagoras
Często w zadaniach dotyczących trójkątów prostokątnych podane są tylko długości dwóch boków. I tu wkracza do akcji Twierdzenie Pitagorasa, które jest Twoim najlepszym przyjacielem w takiej sytuacji! Pamiętaj, że w trójkącie prostokątnym boki tworzące kąt prosty nazywamy przyprostokątnymi (oznaczamy je zazwyczaj jako 'a' i 'b'), a bok leżący naprzeciwko kąta prostego to przeciwprostokątna (zazwyczaj 'c'). Twierdzenie Pitagorasa mówi, że:
a² + b² = c²
Dzięki niemu, znając dwie przyprostokątne, możesz obliczyć przeciwprostokątną, i na odwrót. To pozwala Ci znaleźć brakujący bok, a następnie obliczyć obwód.
Przykład z wykorzystaniem twierdzenia Pitagorasa: Oblicz obwód, znając tylko przyprostokątne
Załóżmy, że mamy trójkąt prostokątny, którego przyprostokątne mają długości 3 cm i 4 cm. Jak obliczyć jego obwód?
- Zidentyfikuj znane boki: Przyprostokątne a = 3 cm, b = 4 cm.
-
Użyj twierdzenia Pitagorasa, aby znaleźć przeciwprostokątną (c):
- a² + b² = c²
- 3² + 4² = c²
- 9 + 16 = c²
- 25 = c²
- c = √25
- c = 5 cm (długość przeciwprostokątnej)
- Teraz, gdy znasz wszystkie boki, zastosuj ogólny wzór na obwód: Obw = a + b + c.
- Podstaw wartości i oblicz: Obw = 3 cm + 4 cm + 5 cm = 12 cm.
Obwód tego trójkąta prostokątnego wynosi 12 cm. Jak widzisz, Pitagoras to naprawdę pomocny przyjaciel!
Najczęstsze pułapki i błędy w zadaniach: Jak ich uniknąć?
Nierówność trójkąta: Czy z każdych trzech boków powstanie trójkąt?
To bardzo ważna zasada, o której często zapominają uczniowie! Nie z każdych trzech odcinków da się zbudować trójkąt. Musi być spełniony warunek zwany nierównością trójkąta: suma długości dwóch dowolnych boków musi być zawsze większa niż długość trzeciego boku. Jeśli ten warunek nie jest spełniony, trójkąt po prostu się "nie zamknie". Na przykład, jeśli masz boki o długościach 2 cm, 3 cm i 6 cm, nie zbudujesz z nich trójkąta, ponieważ 2 + 3 = 5, co jest mniejsze niż 6. Pamiętaj o tym, aby uniknąć błędnych założeń!
Mieszane jednostki: Jak nie popełnić prostego błędu na starcie?
Wspominałem o tym wcześniej, ale to tak częsty błąd, że warto go powtórzyć: zawsze ujednolicaj jednostki przed rozpoczęciem obliczeń! To prosta zasada, która może uratować Cię przed błędnym wynikiem. Wyobraź sobie zadanie, w którym boki trójkąta mają długości: 5 cm, 20 mm i 0.1 dm. Zanim zaczniesz dodawać, przelicz wszystko na jedną, wspólną jednostkę, na przykład centymetry:
- 5 cm (pozostaje bez zmian)
- 20 mm = 2 cm (ponieważ 1 cm = 10 mm)
- 0.1 dm = 1 cm (ponieważ 1 dm = 10 cm)
Teraz możesz dodać: 5 cm + 2 cm + 1 cm = 8 cm. Widzisz, jak łatwo można się pomylić, jeśli się o tym zapomni?
Po co liczymy obwód trójkąta? Praktyczne zastosowania
Planowanie ogrodzenia działki w kształcie trójkąta
Obliczanie obwodu trójkąta to nie tylko teoria szkolna, ale coś, co ma realne zastosowanie w życiu. Wyobraź sobie, że masz działkę w kształcie trójkąta i chcesz ją ogrodzić. Aby kupić odpowiednią ilość siatki lub paneli ogrodzeniowych, musisz dokładnie wiedzieć, jaką długość ma całe ogrodzenie. Właśnie wtedy obliczenie obwodu trójkąta staje się absolutnie niezbędne! To pozwala na precyzyjne zaplanowanie budżetu i uniknięcie niepotrzebnych kosztów.
Przeczytaj również: Działania odwrotne: Twoja supermoc w matematyce! Rozwiąż równania
Zadania z życia codziennego, w których obwód jest niezbędny
- Obszywanie tkanin: Jeśli chcesz obszyć krawędzie trójkątnego obrusu, serwetki czy flagi, musisz znać obwód, aby kupić odpowiednią ilość taśmy lub nici.
- Prace budowlane i remontowe: Architekci i budowlańcy często obliczają obwody trójkątnych elementów konstrukcyjnych, aby określić zapotrzebowanie na materiały, np. listwy wykończeniowe.
- Geodezja: W pomiarach terenowych, zwłaszcza przy wytyczaniu granic działek czy dróg, geodeci wykorzystują obwody figur, w tym trójkątów, do precyzyjnych obliczeń powierzchni i odległości.
- Sztuka i rzemiosło: Tworząc ramki na zdjęcia, mozaiki czy inne dzieła sztuki z trójkątnych elementów, znajomość obwodu pomaga w dokładnym cięciu i dopasowywaniu materiałów.

