W świecie matematyki, gdzie liczby opowiadają swoje historie, dzielenie jest jedną z najbardziej fundamentalnych operacji. Ten artykuł to Twój przewodnik po jej podstawach. Pomogę Ci zrozumieć, czym jest dzielna, a czym dzielnik, jak je bezbłędnie rozróżniać i jak swobodnie rozwiązywać zadania, co jest kluczowe zarówno dla uczniów, jak i dla każdego, kto chce odświeżyć swoją wiedzę.
Dzielna to liczba dzielona, dzielnik to ten, który dzieli poznaj klucz do zrozumienia dzielenia.
- Dzielna (a) to liczba, którą dzielimy, dzielnik (b) to liczba, przez którą dzielimy, a iloraz (c) to wynik.
- Dzielna zawsze występuje jako pierwsza w zapisie działania dzielenia, przed znakiem ":".
- Kardynalna zasada: dzielnik nigdy nie może być równy zero, ponieważ dzielenie przez zero jest niewykonalne.
- Dzielenie z resztą pozwala określić, ile razy dzielnik mieści się w dzielnej i jaka część pozostaje; reszta zawsze musi być mniejsza od dzielnika.
- Skuteczne mnemotechniki i proste triki pomagają raz na zawsze zapamiętać, która liczba jest dzielną, a która dzielnikiem.
- Dzielenie nie jest przemienne ani łączne, a w zadaniach z wieloma działaniami wykonuje się je przed dodawaniem i odejmowaniem.
Zrozumieć dzielenie: dlaczego warto znać dzielną i dzielnika?
Zrozumienie pojęć dzielnej i dzielnika to absolutna podstawa, bez której trudno o swobodne poruszanie się w świecie matematyki. To nie tylko kwestia szkolnych ocen, ale przede wszystkim umiejętność logicznego myślenia i rozwiązywania problemów, które napotykamy na co dzień. W końcu, czy to dzieląc pizzę na równe kawałki, czy obliczając, ile dni zostało do ważnego wydarzenia, zawsze mamy do czynienia z dzieleniem. Solidne opanowanie tych fundamentów otwiera drzwi do dalszej nauki, na przykład o podzielności liczb czy największym wspólnym dzielniku.
Czym jest dzielna, a czym dzielnik? Prosta definicja na start
Zacznijmy od absolutnych podstaw. W każdym działaniu dzielenia, które możemy zapisać jako a : b = c, mamy do czynienia z trzema kluczowymi elementami. Liczba a to nasza dzielna czyli liczba, którą zamierzamy podzielić. Liczba b to dzielnik to ona określa, na ile części lub grup dzielimy naszą dzielną. Natomiast c to iloraz, czyli po prostu wynik naszego dzielenia. Weźmy przykład: 10 : 2 = 5. Tutaj 10 to dzielna, 2 to dzielnik, a 5 to iloraz.
Rola głównych bohaterów: kto jest kim w działaniu a: b = c?
Aby jeszcze lepiej to zrozumieć, wyobraź sobie, że masz pyszny tort i chcesz go podzielić między swoich gości. W tym scenariuszu, tort to nasza dzielna to on jest całością, którą będziemy rozdzielać. Goście to dzielnik to oni determinują, na ile równych części musimy podzielić tort. A każdy kawałek, który dostanie gość, to iloraz wynik sprawiedliwego podziału. Dzielenie to nic innego jak rozdzielanie pewnej całości na równe części lub sprawdzanie, ile razy jedna liczba mieści się w drugiej.
Iloraz i reszta: poznaj pozostałych członków matematycznej rodziny
Jak już wspomniałem, iloraz to wynik dzielenia, czyli to, co otrzymujemy po sprawiedliwym podziale. Ale co, jeśli tortu nie da się podzielić idealnie na równe kawałki dla każdego gościa? Wtedy pojawia się reszta. Dzielenie z resztą to operacja, która pokazuje, ile razy dzielnik w całości mieści się w dzielnej, a także jaka część pozostaje niepodzielona. Ważne jest, aby pamiętać, że reszta zawsze musi być mniejsza od dzielnika. Na przykład, jeśli mamy 7 cukierków i chcemy podzielić je między 2 osoby (7 : 2), każda osoba dostanie 3 cukierki (iloraz), a 1 cukierek zostanie (reszta). Zatem 7 : 2 = 3 reszta 1.
Jak raz na zawsze zapamiętać, która liczba jest która?
Wielu uczniów, a nawet dorosłych, ma problem z bezbłędnym rozróżnianiem dzielnej od dzielnika. To naturalne, zwłaszcza na początku nauki. Jednak prawidłowe zidentyfikowanie tych elementów jest absolutnie kluczowe dla poprawnego wykonania działania. Pomylenie ich miejscami prowadzi do błędnych wyników i nieporozumień. Na szczęście istnieją proste triki i mnemotechniki, które pomogą Ci raz na zawsze zapamiętać, która liczba jest która.
Prosty trik wizualny: dlaczego dzielna zawsze stoi na początku?
Jednym z najprostszych sposobów na zapamiętanie jest obserwacja zapisu. W standardowym działaniu dzielenia, na przykład 12 : 3, dzielna zawsze występuje jako pierwsza, przed znakiem dzielenia (dwukropkiem). To stała pozycja, która nigdy się nie zmienia. Pomyśl o tym jak o głównym bohaterze, który zawsze pojawia się na scenie jako pierwszy. To bardzo prosta, ale niezwykle skuteczna wskazówka wizualna, która może zapobiec wielu pomyłkom.
Mnemotechniki, które działają: wierszyki i skojarzenia do zapamiętania
- Skojarzenie z płciami: Jedna z popularnych mnemotechnik to skojarzenie, że "dzielna" (kobieta) jest zawsze pierwsza, a "dzielnik" (mężczyzna) jest drugi. To proste, humorystyczne skojarzenie, które często pomaga zapamiętać kolejność.
- Rymowanki: Możesz spróbować stworzyć własną rymowankę. Na przykład: "Dzielna jest duża, stoi na początku, dzielnik ją dzieli, bez żadnego smutku." Im bardziej absurdalna lub osobista rymowanka, tym łatwiej ją zapamiętać.
- Historyjki: Stwórz krótką historyjkę. Dzielna to skarb, który trzeba podzielić. Dzielnik to pirat, który ten skarb dzieli. Skarb (dzielna) zawsze jest pierwszy, bo to o niego chodzi.
Zachęcam Cię do eksperymentowania i tworzenia własnych metod. To, co działa dla Ciebie, jest najlepsze!
Najczęstszy błąd: pułapka zamiany miejsc i jak jej unikać
Najczęstszym błędem, jaki widzę u moich uczniów, jest pomylenie dzielnej z dzielnikiem. Ludzie często myślą, że "większa liczba zawsze jest dzielną" lub "dzielimy mniejszą przez większą". To prowadzi do poważnych konsekwencji, ponieważ zamiana miejscami dzielnej i dzielnika całkowicie zmienia wynik działania. Na przykład, 10 : 2 = 5, ale 2 : 10 = 0,2 (lub 0 reszty 2). Różnica jest kolosalna! Zastosowanie wspomnianych mnemotechnik i zwracanie uwagi na stałą pozycję dzielnej w zapisie to najlepszy sposób, aby uniknąć tej pułapki.
Dzielenie w praktyce: od teorii do rozwiązywania zadań
Zrozumienie teorii to jedno, ale prawdziwa magia zaczyna się, gdy potrafimy zastosować tę wiedzę w praktyce. Dzielenie to nie tylko abstrakcyjne działanie, ale narzędzie, które pozwala nam rozwiązywać codzienne problemy. Przejdźmy teraz do konkretnych przykładów, które pokażą Ci, jak swobodnie posługiwać się dzielną i dzielnikiem w różnych sytuacjach.
Proste przykłady krok po kroku: jak poprawnie wykonać dzielenie?
Przyjrzyjmy się kilku podstawowym przykładom dzielenia bez reszty:
-
10 : 2 = ?
- Dzielna: 10
- Dzielnik: 2
- Pytamy: ile razy liczba 2 mieści się w liczbie 10?
- Odpowiedź: 5 razy.
- Iloraz: 5.
-
12 : 3 = ?
- Dzielna: 12
- Dzielnik: 3
- Pytamy: ile razy liczba 3 mieści się w liczbie 12?
- Odpowiedź: 4 razy.
- Iloraz: 4.
-
15 : 5 = ?
- Dzielna: 15
- Dzielnik: 5
- Pytamy: ile razy liczba 5 mieści się w liczbie 15?
- Odpowiedź: 3 razy.
- Iloraz: 3.
Co zrobić, gdy pojawia się "reszta"? Wszystko o dzieleniu z resztą
Dzielenie z resztą jest równie ważne i często spotykane. Pamiętajmy o zasadzie, że reszta musi być zawsze mniejsza od dzielnika. Aby sprawdzić poprawność dzielenia z resztą, możemy użyć wzoru: dzielna = dzielnik × iloraz + reszta. To bardzo przydatne narzędzie do weryfikacji. Oto kilka przykładów:
-
7 : 2 = ?
- Dzielna: 7, Dzielnik: 2
- 2 mieści się w 7 trzy razy (2 × 3 = 6).
- Pozostaje 7 - 6 = 1.
- Iloraz: 3, Reszta: 1. (Sprawdzenie: 2 × 3 + 1 = 7)
-
11 : 3 = ?
- Dzielna: 11, Dzielnik: 3
- 3 mieści się w 11 trzy razy (3 × 3 = 9).
- Pozostaje 11 - 9 = 2.
- Iloraz: 3, Reszta: 2. (Sprawdzenie: 3 × 3 + 2 = 11)
-
17 : 4 = ?
- Dzielna: 17, Dzielnik: 4
- 4 mieści się w 17 cztery razy (4 × 4 = 16).
- Pozostaje 17 - 16 = 1.
- Iloraz: 4, Reszta: 1. (Sprawdzenie: 4 × 4 + 1 = 17)
Sprawdzenie wyniku to podstawa: jak użyć mnożenia, by mieć 100% pewności?
Zawsze powtarzam moim uczniom: sprawdzanie wyniku to podstawa! Mnożenie jest operacją odwrotną do dzielenia, dlatego idealnie nadaje się do weryfikacji. Jeśli masz wątpliwości, czy poprawnie wykonałeś dzielenie, po prostu pomnóż iloraz przez dzielnik. Jeśli wynik zgadza się z dzielną (lub z dzielną minus reszta), to masz pewność, że wszystko jest w porządku.
-
Dla dzielenia bez reszty:
- Przykład: 10 : 2 = 5
- Sprawdzenie:
dzielnik × iloraz = dzielnaczyli 2 × 5 = 10. Wynik się zgadza!
-
Dla dzielenia z resztą:
- Przykład: 7 : 2 = 3 reszta 1
- Sprawdzenie:
dzielnik × iloraz + reszta = dzielnaczyli 2 × 3 + 1 = 6 + 1 = 7. Wynik się zgadza!
Zadania tekstowe z życia wzięte: gdzie na co dzień spotykamy dzielną i dzielnika?
Matematyka jest wszędzie, a dzielenie to jedno z tych działań, które stosujemy intuicyjnie. Oto kilka przykładów zadań tekstowych, które pokazują, jak dzielna i dzielnik pomagają nam w codziennym życiu:
-
Podział przedmiotów: Masz 24 cukierki i chcesz rozdzielić je równo między 6 przyjaciół. Ile cukierków dostanie każdy z nich?
- Dzielna: 24 (liczba cukierków)
- Dzielnik: 6 (liczba przyjaciół)
- Rozwiązanie: 24 : 6 = 4. Każdy przyjaciel dostanie 4 cukierki.
-
Obliczanie czasu: Wiesz, że rok ma 365 dni. Ile to pełnych tygodni?
- Dzielna: 365 (liczba dni)
- Dzielnik: 7 (liczba dni w tygodniu)
- Rozwiązanie: 365 : 7 = 52 reszta 1. To 52 pełne tygodnie i 1 dzień pozostaje.
-
Rozdzielanie kosztów: Cztery osoby wybrały się na wycieczkę i wydały łącznie 120 zł na paliwo. Ile każda osoba powinna zapłacić, jeśli dzielą się kosztami po równo?
- Dzielna: 120 (całkowity koszt)
- Dzielnik: 4 (liczba osób)
- Rozwiązanie: 120 : 4 = 30. Każda osoba powinna zapłacić 30 zł.
Kluczowe zasady, o których nie można zapomnieć
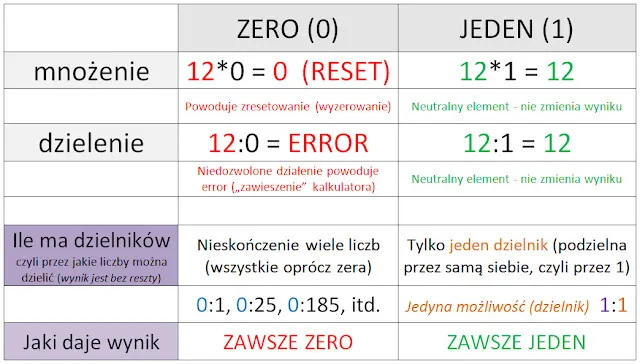
Zrozumienie dzielnej i dzielnika to jeden filar, ale istnieją też inne fundamentalne zasady, które rządzą operacją dzielenia. Ich znajomość jest niezbędna do prawidłowego i bezpiecznego wykonywania działań matematycznych. Pozwól, że przypomnę Ci o najważniejszych z nich.Kardynalna reguła matematyki: dlaczego nigdy nie wolno dzielić przez zero?
To jedna z najważniejszych i najbardziej fundamentalnych zasad w matematyce: nigdy nie wolno dzielić przez zero. Dzielenie przez zero jest operacją niewykonalną i nie ma sensu matematycznego. Wyobraź sobie, że masz 10 jabłek i chcesz je podzielić na zero grup. Jak miałoby to wyglądać? Nie da się tego zrobić. Matematyka opiera się na logice, a dzielenie przez zero prowadzi do sprzeczności i nieokreśloności. Zawsze pamiętaj: dzielnik nigdy nie może być równy zero!
Dzielenie a inne działania: jaka jest prawidłowa kolejność w zadaniach?
Kiedy w jednym zadaniu pojawia się wiele różnych działań, kluczowa jest znajomość prawidłowej kolejności ich wykonywania. Zasada jest prosta: najpierw wykonujemy działania w nawiasach, potem potęgowanie i pierwiastkowanie, następnie mnożenie i dzielenie (w kolejności ich występowania od lewej do prawej), a na końcu dodawanie i odejmowanie (również w kolejności występowania). Na przykład, w działaniu 10 + 6 : 2, najpierw wykonujemy dzielenie: 6 : 2 = 3. Dopiero potem dodajemy: 10 + 3 = 13. Pamiętaj o tym, aby uniknąć błędów!
Przeczytaj również: Sprawdzanie równania: Jak mieć pewność, że wynik jest poprawny?
Czy kolejność ma znaczenie? Słów kilka o przemienności dzielenia
W przeciwieństwie do dodawania (np. 2 + 3 = 3 + 2) i mnożenia (np. 2 × 3 = 3 × 2), dzielenie nie jest przemienne. Oznacza to, że zmiana kolejności dzielnej i dzielnika zmienia wynik działania. Weźmy prosty przykład: 10 : 2 = 5. Jeśli jednak zmienimy kolejność i spróbujemy podzielić 2 : 10, otrzymamy 0,2. Jak widać, wyniki są zupełnie inne. Ta własność jest bardzo ważna i podkreśla, dlaczego tak istotne jest prawidłowe rozróżnianie dzielnej od dzielnika.