Kolejność działań w matematyce: Jak zawsze liczyć poprawnie?

Zrozumienie kolejności działań w matematyce to absolutna podstawa, bez której trudno o poprawne wyniki w obliczeniach. Niezależnie od tego, czy jesteś uczniem, rodzicem pomagającym w nauce, czy po prostu chcesz odświeżyć swoją wiedzę, opanowanie tej hierarchii jest kluczowe do skutecznego rozwiązywania zadań i unikania frustrujących błędów.

Dlaczego kolejność działań jest kluczowa w matematyce?

Dla mnie, jako osoby, która od lat zajmuje się matematyką, jasne jest, że przestrzeganie kolejności działań to absolutny fundament. To nie jest tylko szkolna zasada, ale logiczny system, który gwarantuje, że wszyscy dojdziemy do tego samego, poprawnego wyniku. Nawet drobna pomyłka w tej hierarchii może prowadzić do całkowicie błędnych rezultatów, co w realnym świecie mogłoby mieć poważne konsekwencje od błędnie obliczonego budżetu po źle zaplanowany projekt.

Jak jeden błąd w kolejności może całkowicie zmienić wynik?

To klasyczny przykład, który często pokazuję, aby uzmysłowić, jak ważna jest kolejność działań. Weźmy proste wyrażenie: 5 + 3 * 2. Jeśli zapomnimy o priorytecie mnożenia i dodamy najpierw 5 + 3, otrzymamy 8, a następnie pomnożymy to przez 2, co da nam 16. Wynik jest całkowicie błędny! Poprawne obliczenie to 5 + (3 * 2) = 5 + 6 = 11. Widzisz, jak jeden mały błąd w kolejności zmienia wynik o ponad 40%? To właśnie dlatego ta zasada jest tak krytyczna.

Od szkolnej ławki po codzienne życie gdzie przydają się te zasady?

Może się wydawać, że kolejność działań to tylko teoria, ale w rzeczywistości ma ona mnóstwo praktycznych zastosowań poza salą lekcyjną. Osobiście widzę jej wartość w wielu codziennych sytuacjach:

• Planowanie budżetu domowego: Obliczając wydatki i przychody, często musimy sumować różne kwoty, a następnie odejmować je od dochodów.
• Robienie zakupów z rabatami: Kiedy kupujemy wiele produktów i stosujemy różne rabaty (np. procentowe na cały koszyk, a stałe na pojedyncze produkty), musimy precyzyjnie obliczyć ostateczną cenę.
• Gotowanie i pieczenie: Skalowanie przepisów (np. podwojenie składników) wymaga mnożenia, a potem dodawania, aby uzyskać prawidłowe proporcje.
• Proste majsterkowanie: Obliczanie ilości materiałów, kosztów czy wymiarów często wymaga złożonych działań.

To pokazuje, że matematyka, a w szczególności kolejność działań, to nie tylko abstrakcyjne pojęcia, ale narzędzia, które pomagają nam sprawniej funkcjonować w codziennym życiu.

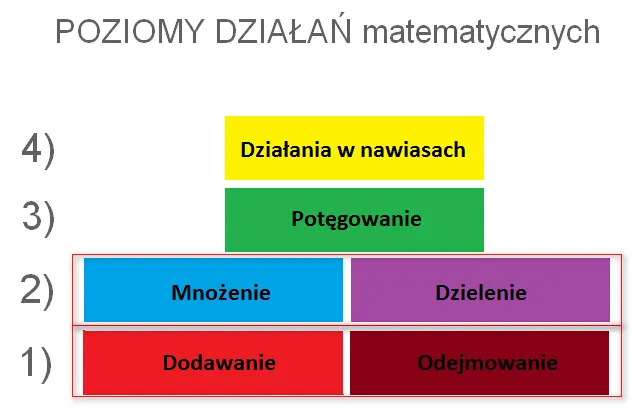
Poznaj 4 kluczowe zasady kolejności działań w matematyce

Matematyka to język precyzji, a jej fundamentem są jasno określone reguły. W kontekście kolejności działań mamy do czynienia z hierarchią, która jest uniwersalna i pozwala nam wszystkim dojść do tego samego, poprawnego rozwiązania. Przyjrzyjmy się czterem kluczowym zasadom, które stanowią kręgosłup każdego złożonego obliczenia.

Krok 1: Nawiasy absolutny priorytet w każdym działaniu

Zawsze powtarzam moim uczniom: nawiasy to król! To one mają bezwzględne pierwszeństwo w każdym wyrażeniu matematycznym. Niezależnie od tego, co znajduje się w nawiasach, musimy wykonać te działania jako pierwsze. Jeśli mamy do czynienia z nawiasami zagnieżdżonymi (nawias w nawiasie), zawsze zaczynamy od tych najbardziej wewnętrznych i stopniowo przechodzimy na zewnątrz. Spójrzmy na przykład:

(5 + 3) * 2

1. Najpierw wykonujemy działanie w nawiasie: 5 + 3 = 8.
2. Następnie podstawiamy wynik do wyrażenia: 8 * 2.
3. Otrzymujemy ostateczny wynik: 16.

Krok 2: Potęgi i pierwiastki druga w hierarchii siła matematyczna

Gdy uporamy się z nawiasami, kolej na potęgowanie i pierwiastkowanie. Te działania zajmują drugie miejsce w hierarchii i są ze sobą równorzędne. Oznacza to, że jeśli w wyrażeniu pojawią się zarówno potęgi, jak i pierwiastki, wykonujemy je w kolejności, w jakiej występują, od lewej do prawej. Oto prosty przykład:

4² + 3

1. Najpierw obliczamy potęgę: 4² = 4 * 4 = 16.
2. Następnie podstawiamy wynik do wyrażenia: 16 + 3.
3. Otrzymujemy ostateczny wynik: 19.

Krok 3: Mnożenie i dzielenie zasada równorzędności od lewej do prawej

Po nawiasach, potęgach i pierwiastkach przychodzi czas na mnożenie i dzielenie. Te dwa działania są trzecie w kolejności i są ze sobą równorzędne. Kluczowa zasada tutaj to: wykonujemy je w kolejności występowania, od lewej do prawej. Nie ma znaczenia, czy najpierw jest mnożenie, czy dzielenie idziemy po prostu od lewej do prawej. Zobaczmy to na przykładzie:

10 / 2 * 3

1. Zaczynamy od lewej: 10 / 2 = 5.
2. Następnie podstawiamy wynik i kontynuujemy: 5 * 3.
3. Otrzymujemy ostateczny wynik: 15.

Krok 4: Dodawanie i odejmowanie ostatni, równie ważny etap obliczeń

Na samym końcu hierarchii znajdują się dodawanie i odejmowanie. Podobnie jak mnożenie i dzielenie, są to działania równorzędne i wykonujemy je w kolejności występowania, od lewej do prawej. To ostatni etap, który prowadzi nas do finalnego wyniku. Przykład:

15 - 5 + 2

1. Zaczynamy od lewej: 15 - 5 = 10.
2. Następnie podstawiamy wynik i kontynuujemy: 10 + 2.
3. Otrzymujemy ostateczny wynik: 12.

Kolejność działań w praktyce: Przykłady krok po kroku

Poznanie zasad to jedno, ale prawdziwe mistrzostwo osiąga się poprzez praktykę. Przygotowałem dla Ciebie serię przykładów, które pozwolą Ci przećwiczyć i utrwalić nabytą wiedzę. Zaczniemy od prostych działań, a potem stopniowo zwiększymy poziom trudności, abyś poczuł się pewnie w obliczeniach.

Rozgrzewka: Proste przykłady z mnożeniem i dodawaniem

1. Przykład: 7 + 2 * 4
   • Krok 1: Najpierw wykonujemy mnożenie, ponieważ ma wyższy priorytet niż dodawanie: 2 * 4 = 8.
   • Krok 2: Następnie dodajemy wynik: 7 + 8 = 15.
   • Wynik: 15
2. Przykład: 12 / 3 - 1
   • Krok 1: Najpierw wykonujemy dzielenie, ponieważ ma wyższy priorytet niż odejmowanie: 12 / 3 = 4.
   • Krok 2: Następnie odejmujemy: 4 - 1 = 3.
   • Wynik: 3

Poziom wyżej: Działania z nawiasami jak je poprawnie rozwiązywać?

Nawiasy to Twój najlepszy przyjaciel w złożonych wyrażeniach wskazują, co należy zrobić najpierw. Pamiętaj o zasadzie "najpierw nawiasy wewnętrzne"!

1. Przykład: (10 - 4) * 5
   • Krok 1: Zaczynamy od działania w nawiasie: 10 - 4 = 6.
   • Krok 2: Następnie mnożymy wynik przez 5: 6 * 5 = 30.
   • Wynik: 30
2. Przykład: 3 * (2 + (8 / 4))
   • Krok 1: Zaczynamy od najbardziej wewnętrznego nawiasu, a w nim od dzielenia: 8 / 4 = 2.
   • Krok 2: Podstawiamy wynik do wewnętrznego nawiasu i wykonujemy dodawanie: 2 + 2 = 4.
   • Krok 3: Podstawiamy wynik do zewnętrznego nawiasu i wykonujemy mnożenie: 3 * 4 = 12.
   • Wynik: 12

Wyzwanie mistrza: Złożone wyrażenia z potęgami i wieloma działaniami

Teraz czas na prawdziwe wyzwanie! Połączymy wszystkie zasady, aby rozwiązać bardziej skomplikowane wyrażenia. To właśnie tutaj widać, jak kluczowe jest konsekwentne przestrzeganie hierarchii.

1. Przykład: 20 - (3 * 2² + 5) / 3
   • Krok 1: Zaczynamy od nawiasu. Wewnątrz nawiasu najpierw potęgowanie: 2² = 4.
   • Krok 2: Nadal w nawiasie, teraz mnożenie: 3 * 4 = 12.
   • Krok 3: Nadal w nawiasie, teraz dodawanie: 12 + 5 = 17.
   • Krok 4: Całe wyrażenie staje się: 20 - 17 / 3. Teraz dzielenie: 17 / 3 = 5.666... (zaokrąglimy do dwóch miejsc po przecinku dla uproszczenia, w rzeczywistości wynik może być ułamkiem).
   • Krok 5: Na koniec odejmowanie: 20 - 5.67 = 14.33.
   • Wynik: 14.33 (lub 14 i 1/3, jeśli zostawimy w ułamku).

Najczęstsze pułapki i błędy w kolejności działań

Nawet doświadczeni matematycy czasem popełniają błędy, zwłaszcza gdy są rozproszeni. Z mojego doświadczenia wiem, że pewne pomyłki powtarzają się częściej niż inne. Świadomość tych pułapek to już połowa sukcesu w ich unikaniu. Przyjrzyjmy się najczęstszym błędom, abyś mógł ich świadomie unikać.

Błąd #1: Zapominanie o zasadzie "od lewej do prawej" przy mnożeniu i dzieleniu

To bardzo podstępny błąd, który często pojawia się, gdy w wyrażeniu mamy kilka działań równorzędnych (np. dodawanie i odejmowanie lub mnożenie i dzielenie). Ludzie mają tendencję do "grupowania" liczb w sposób, który wydaje im się intuicyjny, zamiast ściśle trzymać się zasady "od lewej do prawej". Weźmy przykład 10 - 4 + 2. Błędne myślenie prowadzi do obliczenia 10 - (4 + 2) = 10 - 6 = 4. To jest nieprawidłowe! Prawidłowa kolejność to (10 - 4) + 2 = 6 + 2 = 8. Pamiętaj, że gdy działania mają ten sam priorytet, zawsze idziemy od lewej do prawej.

Błąd #2: Wykonywanie dodawania przed mnożeniem klasyczna pomyłka

Ten błąd to absolutny klasyk i jeden z najczęściej popełnianych przez początkujących. Wrócimy do naszego przykładu: 5 + 3 * 2. Widząc 5 + 3 na początku, wiele osób instynktownie wykonuje to dodawanie jako pierwsze, otrzymując 8 * 2 = 16. Niestety, jest to błąd! Mnożenie ma wyższy priorytet niż dodawanie, dlatego najpierw musimy obliczyć 3 * 2 = 6, a dopiero potem dodać 5, co daje nam poprawny wynik 11. Zawsze, ale to zawsze, najpierw mnożenie i dzielenie, potem dodawanie i odejmowanie.

Błąd #3: Gubienie się w nawiasach jak zachować porządek w obliczeniach?

Im bardziej złożone wyrażenie, tym więcej nawiasów, a co za tym idzie większe ryzyko pomyłki. Gubienie się w nawiasach, zwłaszcza tych zagnieżdżonych, to częsty problem. Kluczem jest metodyczne podejście: zawsze zaczynamy od nawiasów najbardziej wewnętrznych i krok po kroku, systematycznie, rozwiązujemy je, aż dojdziemy do nawiasów zewnętrznych. Traktuj każdy nawias jako mini-zadanie, które musisz rozwiązać, zanim przejdziesz dalej. To pomaga zachować porządek i unikać błędów.

Zawsze zwracaj uwagę na położenie nawiasów, zwłaszcza przy potęgowaniu liczb ujemnych! Pamiętaj, że -3² to -9 (bo potęgujemy tylko trójkę, a minus zostaje), natomiast (-3)² to 9 (bo potęgujemy całą liczbę ujemną).

Mnemotechniki i triki na zapamiętanie kolejności działań

Wiem, że zapamiętanie wszystkich zasad może być na początku wyzwaniem. Dlatego chcę podzielić się z Wami kilkoma sprawdzonymi mnemotechnikami i trikami, które pomogą Wam utrwalić kolejność działań w pamięci. Sam często polecam je moim uczniom, bo wiem, że działają!

Stwórz własną "piramidę działań" wizualny sposób na naukę

Jednym z najskuteczniejszych sposobów na zapamiętanie hierarchii działań jest stworzenie wizualnej "piramidy kolejności działań". Wyobraź sobie piramidę, na której szczycie znajdują się działania o najwyższym priorytecie, a na dole te o najniższym. Możesz narysować ją na kartce lub po prostu wizualizować w głowie:

1. Szczyt: Nawiasy
2. Poniżej: Potęgi i pierwiastki
3. Jeszcze niżej: Mnożenie i dzielenie (na tym samym poziomie)
4. Podstawa: Dodawanie i odejmowanie (na tym samym poziomie)

Taka piramida jasno pokazuje, co ma pierwszeństwo. To doskonała pomoc wizualna, która utrwala kolejność w pamięci i pomaga szybko przypomnieć sobie zasady podczas rozwiązywania zadań.

Rymowanki i skojarzenia jak kreatywnie utrwalić zasady?

Kreatywne mnemotechniki, takie jak rymowanki czy skojarzenia, to świetny sposób na zapamiętanie skomplikowanych informacji. W Polsce nie mamy tak popularnych akronimów jak anglosaskie PEMDAS czy BODMAS, ale nic nie stoi na przeszkodzie, by stworzyć własne! Możesz wymyślić krótkie zdanie, w którym pierwsze litery słów odpowiadają kolejności działań. Na przykład, dla uproszczenia:

Na Początku Mnożymy Dodajemy

Oczywiście, to bardzo uproszczona wersja, która pomija pierwiastki i odejmowanie, ale pokazuje ideę. Możesz stworzyć bardziej rozbudowaną rymowankę, która obejmie wszystkie elementy hierarchii, np.: "Nawiasy Potęgują, Mnożą, Dzielą, Dodają, Odejmują". Im bardziej zabawna i osobista będzie Twoja mnemotechnika, tym łatwiej ją zapamiętasz!

Przeczytaj również: Jak rozwiązać równanie? Spróbuj zgadnąć! Proste metody

Kolejność działań w życiu codziennym: Zadania z treścią

Matematyka to nie tylko cyfry i abstrakcyjne wzory. To także narzędzie do rozwiązywania problemów z życia wziętych. Zrozumienie kolejności działań jest niezwykle przydatne, gdy musimy przekształcić realny scenariusz w matematyczne wyrażenie i poprawnie je obliczyć. Pokażę Ci to na dwóch praktycznych przykładach.

Przykład z życia wzięty: Jak obliczyć koszt zakupów z rabatem?

Wyobraź sobie, że idziesz na zakupy. Kupiłeś 3 zeszyty po 5 zł każdy i 2 długopisy po 3 zł każdy. Przy kasie okazało się, że masz kupon na 10 zł rabatu na całe zakupy. Ile ostatecznie zapłaciłeś?

Aby poprawnie obliczyć koszt, musimy zastosować kolejność działań:

1. Oblicz koszt zeszytów: 3 * 5 zł = 15 zł
2. Oblicz koszt długopisów: 2 * 3 zł = 6 zł
3. Oblicz łączny koszt przed rabatem: 15 zł + 6 zł = 21 zł
4. Odejmij rabat: 21 zł - 10 zł = 11 zł

Możemy to zapisać w jednym wyrażeniu matematycznym: (3 * 5) + (2 * 3) - 10

• (3 * 5) + (2 * 3) - 10
• 15 + 6 - 10 (najpierw mnożenie w nawiasach)
• 21 - 10 (następnie dodawanie)
• 11 (na koniec odejmowanie)

Zapłaciłeś 11 zł. Bez znajomości kolejności działań łatwo byłoby pomylić się i np. odjąć rabat od ceny zeszytów, zanim dodamy długopisy.

Planowanie podróży: Kolejność działań w obliczaniu czasu i dystansu

Planujesz podróż samochodem. Przez pierwsze 2 godziny jedziesz z prędkością 80 km/h, a potem przez 1 godzinę z prędkością 60 km/h. Ile kilometrów przejechałeś łącznie?

Tutaj również musimy przestrzegać kolejności działań, aby uzyskać poprawny dystans:

1. Oblicz dystans z pierwszej części podróży: 2 h * 80 km/h = 160 km
2. Oblicz dystans z drugiej części podróży: 1 h * 60 km/h = 60 km
3. Oblicz łączny dystans: 160 km + 60 km = 220 km

W formie wyrażenia matematycznego wygląda to tak: (2 * 80) + (1 * 60)

• (2 * 80) + (1 * 60)
• 160 + 60 (najpierw mnożenie w nawiasach)
• 220 (następnie dodawanie)

Przejechałeś łącznie 220 km. Gdybyśmy nie przestrzegali kolejności działań, moglibyśmy np. dodać godziny, a potem pomnożyć przez jedną z prędkości, co dałoby całkowicie błędny wynik.