Zrozumienie funkcji sinus to podstawa w świecie matematyki i wielu dziedzinach nauki. Ta pozornie skomplikowana funkcja trygonometryczna jest w rzeczywistości kluczem do opisywania zjawisk falowych, analizowania drgań czy projektowania konstrukcji. Jako Alan Szymczak, pokażę Ci, jak krok po kroku opanować obliczanie sinusa, niezależnie od tego, czy masz do czynienia z prostym trójkątem, czy złożonym układem współrzędnych.
Sinus: jak go obliczyć krok po kroku najważniejsze informacje w pigułce.
- Sinus to funkcja trygonometryczna definiowana jako stosunek przyprostokątnej leżącej naprzeciwko danego kąta do przeciwprostokątnej w trójkącie prostokątnym.
- Można go obliczyć w trójkącie prostokątnym (dla kątów ostrych) lub za pomocą koła trygonometrycznego (dla dowolnych kątów).
- Wartości sinusa dla kątów charakterystycznych (0°, 30°, 45°, 60°, 90°) należy znać na pamięć.
- Do obliczeń używaj kalkulatora naukowego, zawsze upewniając się, że jest ustawiony w trybie stopni (DEG).
- Dla kątów większych niż 90° stosuje się koło trygonometryczne i wzory redukcyjne.
- Najczęstsze błędy to mylenie boków w trójkącie i niewłaściwy tryb kalkulatora.
Prosta definicja, która rozjaśni Ci wszystko
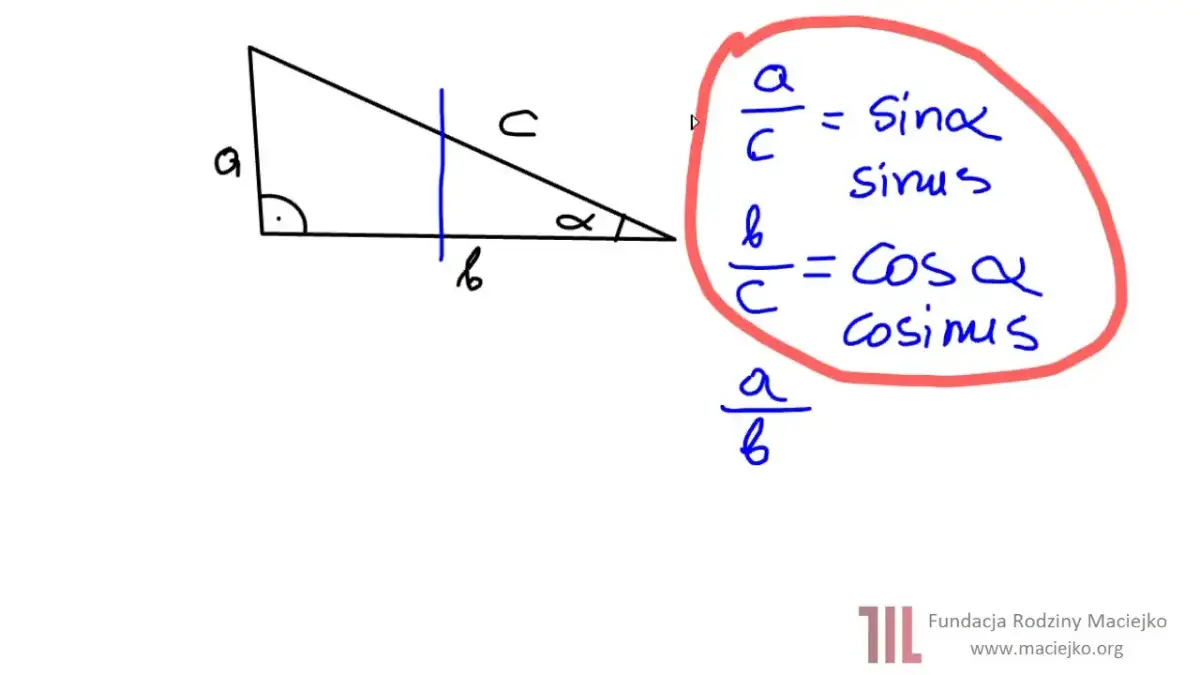
Zacznijmy od podstaw. Funkcja sinus, w skrócie sin, to jedna z kluczowych funkcji trygonometrycznych. Dla dowolnego kąta ostrego (czyli mniejszego niż 90°) w trójkącie prostokątnym, sinus jest definiowany jako stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej. Mówiąc prościej, jeśli masz kąt α, a naprzeciwko niego leży bok o długości 'a', a najdłuższy bok (przeciwprostokątna) ma długość 'c', to sinus tego kąta obliczasz ze wzoru:
sin(α) = a/c
Gdzie 'a' to długość przyprostokątnej leżącej naprzeciwko kąta α, a 'c' to długość przeciwprostokątnej. To naprawdę proste, gdy tylko poprawnie zidentyfikujesz te dwa boki.
Gdzie w praktyce spotkasz się z sinusem od szkoły po życie codzienne
Zrozumienie sinusa wykracza daleko poza salę lekcyjną. W fizyce jest on niezbędny do opisywania fal (dźwiękowych, świetlnych, radiowych), drgań czy rozkładu sił. Inżynierowie używają go przy projektowaniu mostów i budynków, aby obliczyć naprężenia i stabilność konstrukcji. Nawigacja, zarówno morska, jak i lotnicza, opiera się na trygonometrii do wyznaczania pozycji i kursu. Nawet w grafice komputerowej i animacji sinus pomaga tworzyć płynne ruchy i realistyczne efekty, na przykład modelując ruch wahadła czy falowanie wody. Jak widzisz, sinus jest wszędzie, dlatego warto go dobrze poznać.
Jak obliczyć sinus w trójkącie prostokątnym?
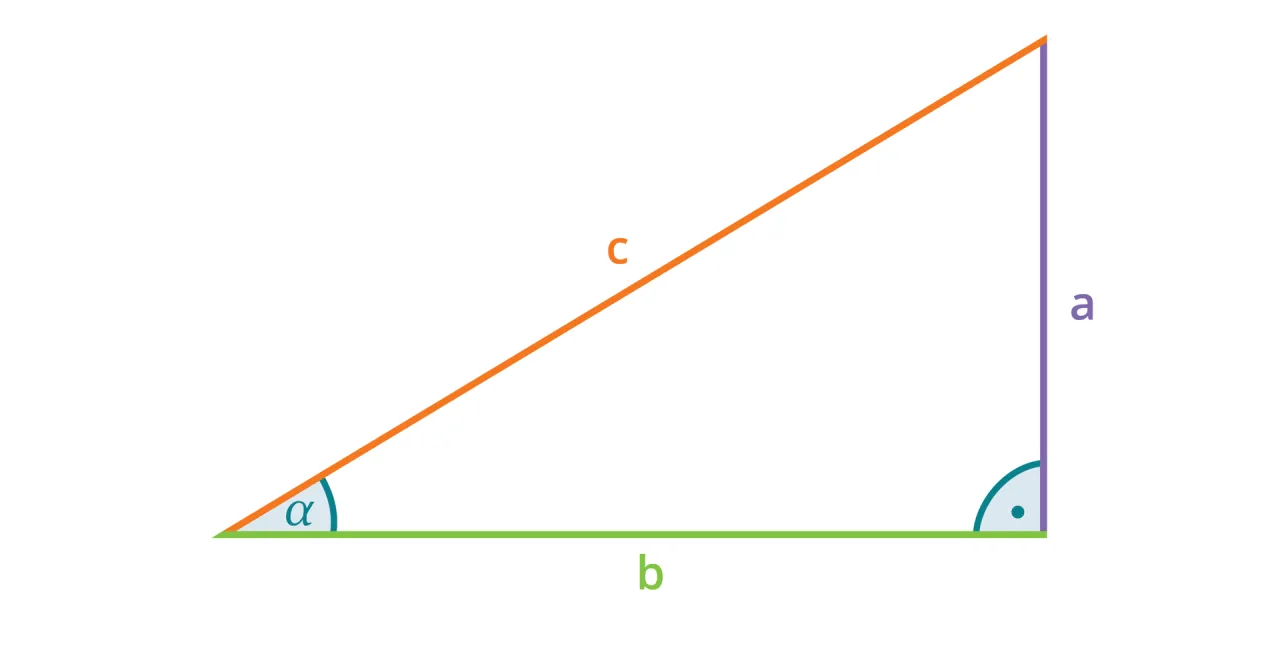
Krok 1: Zidentyfikuj kluczowe boki „ten naprzeciw” i „ten najdłuższy”
Pierwszym i najważniejszym krokiem jest prawidłowe zidentyfikowanie boków w trójkącie prostokątnym. Zawsze pamiętaj, że przeciwprostokątna to najdłuższy bok trójkąta i zawsze leży naprzeciwko kąta prostego (90°). To jest nasze 'c'. Następnie musisz znaleźć przyprostokątną leżącą naprzeciwko kąta, którego sinus chcesz obliczyć. Jeśli rozważamy kąt α, to przyprostokątna leżąca "po drugiej stronie" tego kąta to nasze 'a'. Poprawne rozróżnienie tych dwóch boków jest absolutnie kluczowe, bo pomyłka na tym etapie oznacza błędny wynik.
Krok 2: Zastosuj fundamentalny wzór, który zawsze działa
Gdy już poprawnie zidentyfikujesz długości przyprostokątnej 'a' (leżącej naprzeciwko kąta) i przeciwprostokątnej 'c', wystarczy podstawić te wartości do podstawowego wzoru: sin(α) = a/c. To jest uniwersalna zasada dla wszystkich kątów ostrych w trójkącie prostokątnym. Pamiętaj, że wynik sinusa zawsze będzie liczbą z przedziału od 0 do 1 (dla kątów ostrych), ponieważ przyprostokątna nigdy nie może być dłuższa niż przeciwprostokątna.
Praktyczny przykład: Obliczamy sinus kąta alfa krok po kroku
Wyobraź sobie trójkąt prostokątny o bokach 3, 4 i 5. Wiemy, że 5 to przeciwprostokątna, bo jest najdłuższym bokiem. Załóżmy, że chcemy obliczyć sinus kąta α, który leży naprzeciwko boku o długości 3.
- Zidentyfikuj przeciwprostokątną (c): W naszym trójkącie najdłuższy bok to 5. Zatem c = 5.
- Zidentyfikuj przyprostokątną naprzeciwko kąta (a): Kąt α leży naprzeciwko boku o długości 3. Zatem a = 3.
- Zastosuj wzór: Podstawiamy wartości do wzoru sin(α) = a/c.
- Wykonaj obliczenia: sin(α) = 3/5 = 0.6.
W ten sposób, krok po kroku, obliczyliśmy sinus kąta α, który wynosi 0.6. Proste, prawda?
Wartości sinusa dla kluczowych kątów co warto zapamiętać?
Tabela z gotowymi wynikami dla 0°, 30°, 45°, 60° i 90°
W matematyce, zwłaszcza na poziomie szkolnym, często spotkasz się z tak zwanymi "kątami charakterystycznymi". Wartości sinusa dla tych kątów dobrze jest znać na pamięć, ponieważ pojawiają się w wielu zadaniach. Oto one:
| Kąt | sin(Kąt) |
|---|---|
| 0° | 0 |
| 30° | 1/2 |
| 45° | √2/2 |
| 60° | √3/2 |
| 90° | 1 |
Zapamiętanie tych wartości znacząco przyspieszy Twoje obliczenia i pomoże w rozwiązywaniu zadań bez konieczności sięgania po kalkulator.
Prosty trik na zapamiętanie tych wartości bez wkuwania
Wiem, że zapamiętywanie tabel może być nużące. Na szczęście istnieje sprytny trik, który pozwala odtworzyć wartości sinusa dla kątów 0°, 30°, 45°, 60° i 90° bez wkuwania. Wystarczy zapamiętać wzór √(n)/2, gdzie 'n' przyjmuje wartości od 0 do 4:
- Dla 0°: n=0, więc sin(0°) = √(0)/2 = 0/2 = 0
- Dla 30°: n=1, więc sin(30°) = √(1)/2 = 1/2
- Dla 45°: n=2, więc sin(45°) = √(2)/2 = √2/2
- Dla 60°: n=3, więc sin(60°) = √(3)/2 = √3/2
- Dla 90°: n=4, więc sin(90°) = √(4)/2 = 2/2 = 1
Ten prosty wzór to świetna mnemotechnika, która pozwoli Ci szybko przypomnieć sobie te kluczowe wartości.
Sinus dla kątów większych niż 90°: przewodnik po kole trygonometrycznym
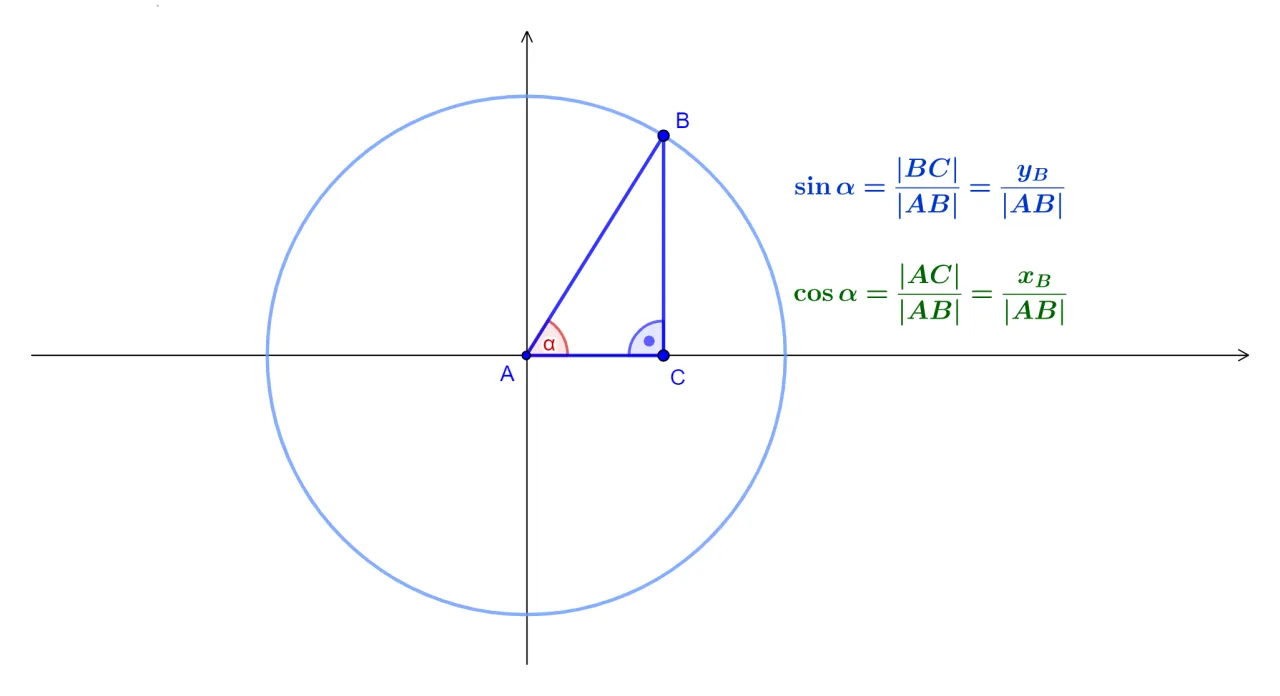
Czym jest koło trygonometryczne i jak ułatwia ono obliczenia?
Kiedy mówimy o kątach większych niż 90° (czyli rozwartych, wklęsłych lub ujemnych), trójkąt prostokątny przestaje być wystarczający. Wtedy na scenę wkracza koło trygonometryczne, znane również jako okrąg jednostkowy. Jest to okrąg o promieniu równym 1, umieszczony w układzie współrzędnych kartezjańskich, ze środkiem w punkcie (0,0). Kąt mierzymy od dodatniej półosi X, obracając się przeciwnie do ruchu wskazówek zegara. Kluczowe jest to, że dla dowolnego kąta, wartość sinusa jest równa współrzędnej 'y' punktu przecięcia końcowego ramienia kąta z tym okręgiem. To uniwersalna definicja, która działa dla każdego kąta.
Znajdowanie sinusa w układzie współrzędnych uniwersalna metoda
Wyznaczanie sinusa za pomocą koła trygonometrycznego jest bardzo intuicyjne. Oto jak to zrobić krok po kroku:
- Narysuj koło trygonometryczne: Okrąg o promieniu 1 z początkiem w (0,0).
- Zaznacz kąt: Odmierz dany kąt (np. 150°) od dodatniej półosi X, obracając się przeciwnie do ruchu wskazówek zegara.
- Znajdź punkt przecięcia: Zlokalizuj punkt, w którym ramię kąta przecina okrąg.
- Odczytaj współrzędną Y: Wartość współrzędnej 'y' tego punktu to właśnie sinus danego kąta.
Na przykład, dla kąta 150°, punkt przecięcia z okręgiem będzie miał współrzędne (-√3/2, 1/2). Zatem sin(150°) = 1/2. Jak widać, koło trygonometryczne pozwala na wizualizację i odczytanie wartości sinusa dla kątów, których nie da się "zmieścić" w trójkącie prostokątnym.
Wzory redukcyjne w akcji: Sprytny sposób na kąty rozwarte i ujemne
Wzory redukcyjne to potężne narzędzie, które pozwala sprowadzić obliczanie sinusa dla kątów większych niż 90° (lub ujemnych) do obliczeń dla kąta ostrego. Dzięki nim nie musisz za każdym razem rysować koła trygonometrycznego. Oto kilka najważniejszych wzorów dla sinusa, które osobiście uważam za najbardziej przydatne:
- sin(180° - α) = sin(α): Jeśli masz kąt w drugiej ćwiartce (np. 150°), możesz go sprowadzić do kąta ostrego. sin(150°) = sin(180° - 30°) = sin(30°) = 1/2.
- sin(180° + α) = -sin(α): Dla kątów w trzeciej ćwiartce (np. 210°), sinus będzie ujemny. sin(210°) = sin(180° + 30°) = -sin(30°) = -1/2.
- sin(360° - α) = -sin(α): Dla kątów w czwartej ćwiartce (np. 330°), sinus również jest ujemny. sin(330°) = sin(360° - 30°) = -sin(30°) = -1/2.
Pamiętaj, że znak sinusa zależy od ćwiartki, w której znajduje się końcowe ramię kąta. W I i II ćwiartce sinus jest dodatni, a w III i IV ujemny. Wzory redukcyjne automatycznie uwzględniają ten znak, co jest niezwykle wygodne.
Kalkulator i inne narzędzia: jak poprawnie obliczyć sinus?
Kalkulator naukowy: Ustawienie, które chroni przed 99% błędów (DEG vs RAD)
Kalkulator naukowy to Twój najlepszy przyjaciel przy obliczaniu sinusa, ale tylko wtedy, gdy jest poprawnie ustawiony! To jest punkt, w którym widzę najwięcej błędów u moich uczniów. Absolutnie kluczowe jest, aby kalkulator był ustawiony w trybie 'DEG' (degrees - stopnie). Większość zadań w szkole i na studiach wymaga podawania kątów w stopniach, a jeśli Twój kalkulator jest w trybie 'RAD' (radiany) lub 'GRAD' (gradusy), dostaniesz zupełnie inny, błędny wynik. Zawsze sprawdź mały wskaźnik na ekranie kalkulatora (zazwyczaj DEG, DRG, R lub G) i w razie potrzeby zmień go za pomocą przycisku 'MODE' lub 'DRG'. To naprawdę uratuje Cię przed frustracją i niepoprawnymi odpowiedziami.
Darmowe kalkulatory online Twoi cyfrowi pomocnicy w matematyce
W dzisiejszych czasach nie musisz mieć fizycznego kalkulatora naukowego, aby obliczyć sinus. Istnieje mnóstwo darmowych kalkulatorów online oraz aplikacji mobilnych, które oferują tę funkcję. Są one niezwykle wygodne, zwłaszcza gdy potrzebujesz szybkiego sprawdzenia wyniku. Wyszukiwarki internetowe, takie jak Google, często mają wbudowane kalkulatory trygonometryczne. Pamiętaj jednak, aby zawsze sprawdzić, czy taki kalkulator online również jest ustawiony w trybie stopni (DEG), jeśli podajesz kąty w stopniach. To samo dotyczy aplikacji na smartfony upewnij się, że znasz ich ustawienia.
A co, jeśli nie masz kalkulatora? Tradycyjne metody, które wciąż działają
Co zrobić, jeśli nie masz pod ręką kalkulatora? Nie panikuj! Dla kątów charakterystycznych (0°, 30°, 45°, 60°, 90°) możesz skorzystać z tabelki, którą omówiliśmy wcześniej, lub z prostego triku z pierwiastkami. To najszybsza metoda. W przeszłości, gdy kalkulatory nie były powszechne, używano również tablic trygonometrycznych obszernych książek zawierających wartości funkcji trygonometrycznych dla wielu kątów. Choć dziś rzadziej stosowane, wciąż są one tradycyjną i skuteczną metodą, która może być wymagana w niektórych specyficznych sytuacjach, np. na egzaminach, gdzie kalkulatory są zabronione.
Najczęstsze błędy przy obliczaniu sinusa i jak ich unikać?
Błąd #1: Mylenie przyprostokątnej przeciwległej z przyległą
To jeden z najczęstszych błędów, jakie widzę. W trójkącie prostokątnym mamy dwie przyprostokątne: jedną leżącą naprzeciwko danego kąta (to nasze 'a' w sin(α) = a/c) i drugą leżącą przy kącie (przyległą). Często uczniowie mylą te dwie przyprostokątne, co oczywiście prowadzi do błędnego wyniku. Aby tego uniknąć, zawsze wizualizuj sobie kąt i zadaj sobie pytanie: "Który bok jest po drugiej stronie tego kąta?". Ten bok to zawsze przyprostokątna przeciwległa. Przeciwprostokątna (najdłuższy bok) jest zawsze łatwa do zidentyfikowania, więc skup się na właściwym wyborze przyprostokątnej.
Błąd #2: Niewłaściwy tryb w kalkulatorze cichy zabójca dobrych wyników
Już o tym wspominałem, ale muszę to powtórzyć, bo to prawdziwy "cichy zabójca" dobrych wyników. Użycie trybu 'RAD' (radiany) zamiast 'DEG' (stopnie) w kalkulatorze naukowym jest źródłem niezliczonych błędów. Wynika to z tego, że radiany i stopnie to dwie różne jednostki miary kąta. Na przykład, sin(30°) to 0.5, ale sin(30 radianów) to zupełnie inna wartość (-0.988...). Zawsze, ale to zawsze, upewnij się, że Twój kalkulator jest w trybie 'DEG', zanim zaczniesz obliczenia. To nawyk, który warto sobie wyrobić.
Przeczytaj również: Opanuj litery greckie w matematyce: Klucz do wzorów!
Błąd #3: Zapominanie o minusie przy kątach z III i IV ćwiartki
Kiedy pracujesz z kołem trygonometrycznym i kątami większymi niż 90°, łatwo zapomnieć o znaku sinusa. Pamiętaj, że sinus jest współrzędną 'y' punktu na okręgu. W I i II ćwiartce (kąty od 0° do 180°) współrzędna 'y' jest dodatnia, więc sinus jest dodatni. Jednak w III i IV ćwiartce (kąty od 180° do 360°) współrzędna 'y' jest ujemna, co oznacza, że sinus przyjmuje wartości ujemne. Jeśli używasz wzorów redukcyjnych, one automatycznie uwzględnią ten znak. Jeśli rysujesz koło, po prostu odczytaj współrzędną 'y' z odpowiednim znakiem. To drobiazg, ale ma ogromne znaczenie dla poprawności wyniku.