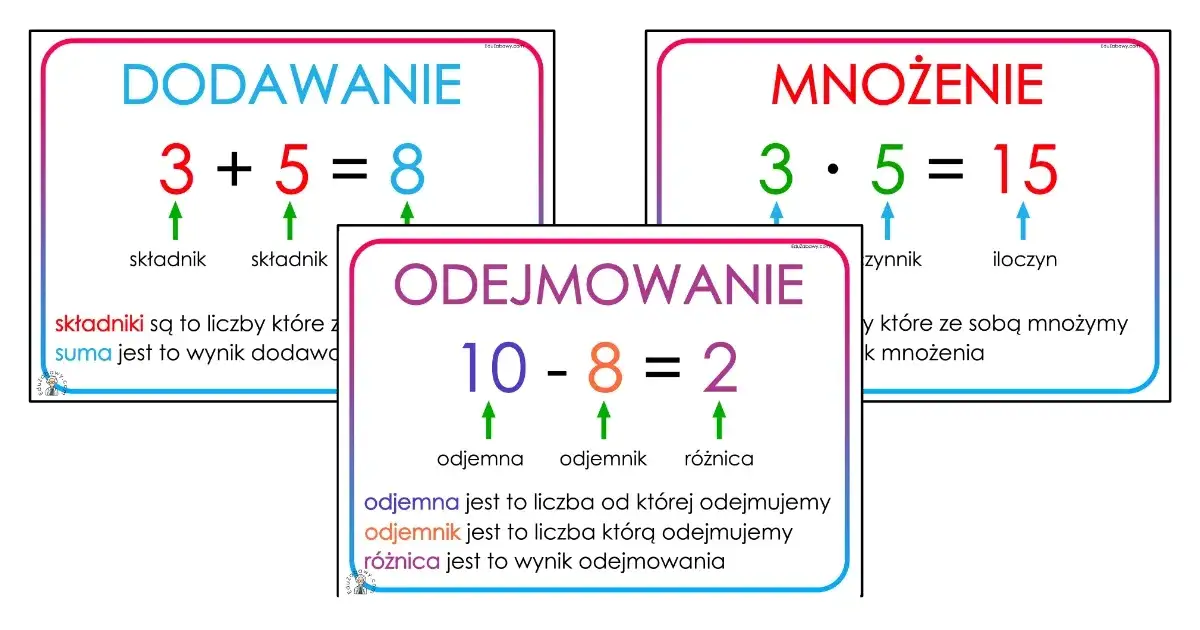
Matematyczne nazwy działań: składniki, czynniki i inne klucz do zrozumienia podstaw
- W dodawaniu liczby nazywamy składnikami, a wynik sumą.
- W odejmowaniu używamy terminów odjemna, odjemnik i różnica.
- Mnożenie ma czynniki i iloczyn; pamiętaj, że "składniki mnożenia" to błąd.
- W dzieleniu występują dzielna, dzielnik i iloraz.
- Każde działanie ma swoje unikalne nazwy, co jest ważne dla precyzji w matematyce.
- Kolejność liczb ma znaczenie w odejmowaniu i dzieleniu, ale nie w dodawaniu i mnożeniu.
Dlaczego nazwy w matematyce są tak ważne?
Jako Alan Szymczak, wielokrotnie widziałem, jak precyzyjne nazewnictwo potrafi ułatwić naukę matematyki. Wyobraź sobie, że próbujesz zbudować coś z klocków, ale nie znasz nazw poszczególnych elementów byłoby to bardzo trudne! Podobnie jest w matematyce. Kiedy uczeń zna i poprawnie używa terminów takich jak "składnik" czy "iloczyn", łatwiej mu zrozumieć treść zadania, precyzyjniej komunikować się z nauczycielem czy kolegami, a także budować solidne podstawy do rozwiązywania bardziej złożonych problemów. To nie jest tylko kwestia zapamiętywania słówek, ale przede wszystkim budowania logicznego myślenia i precyzji, które są esencją królowej nauk.
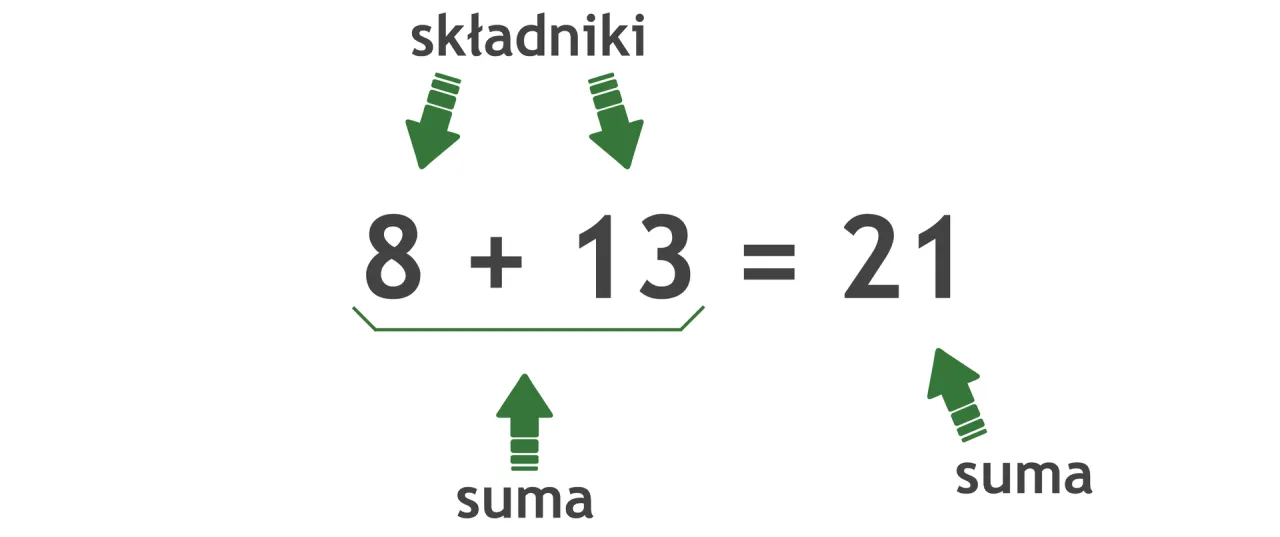
Dodawanie bez tajemnic: składniki i suma
Czym jest składnik? Definicja i proste przykłady
Zacznijmy od dodawania, które jest często pierwszym działaniem, jakie poznajemy. W dodawaniu liczby, które ze sobą łączymy, aby otrzymać większą całość, nazywamy składnikami. To takie "cegiełki", które budują naszą sumę. Na przykład, jeśli mamy działanie 3 + 5 = 8, to liczby 3 i 5 są właśnie składnikami. Inny przykład to 10 + 20 = 30, gdzie 10 i 20 to składniki.
Co nazywamy sumą i jak ją poprawnie obliczyć?
Gdy już połączymy nasze składniki, otrzymujemy sumę. Suma to nic innego jak wynik dodawania. Jest to ostateczny efekt połączenia wszystkich składników. W przykładzie 7 + 2 = 9, liczba 9 to suma. Podobnie, w działaniu 15 + 5 = 20, liczba 20 jest sumą. Obliczenie sumy polega po prostu na wykonaniu dodawania.
Kluczowa zasada: Dlaczego w dodawaniu kolejność nie ma znaczenia?
Jedną z najfajniejszych cech dodawania jest to, że kolejność składników nie wpływa na wynik. Mówimy, że dodawanie jest przemienne. To oznacza, że czy dodasz 5 + 3, czy 3 + 5, wynik zawsze będzie ten sam, czyli 8. To bardzo przydatna zasada, która ułatwia liczenie i pozwala na elastyczne podejście do rozwiązywania problemów.

Odejmowanie krok po kroku: odjemna, odjemnik i różnica
Przejdźmy teraz do odejmowania, które jest działaniem odwrotnym do dodawania. Tutaj nazewnictwo jest równie precyzyjne, a kolejność liczb ma już ogromne znaczenie.
Odjemna: Liczba, od której zaczynamy
W odejmowaniu, liczba, od której "zabieramy" inną liczbę, nazywana jest odjemną. Jest to nasza początkowa wartość. W działaniu 10 - 4 = 6, liczba 10 to odjemna. To od niej zaczynamy całe odejmowanie.
Odjemnik: Liczba, którą "zabieramy"
Natomiast liczba, którą "zabieramy" od odjemnej, to odjemnik. To właśnie ta wartość jest odejmowana. W naszym przykładzie 10 - 4 = 6, liczba 4 to odjemnik. Myślę o nim jak o części, którą usuwamy z całości.
Różnica: Jaki jest efekt końcowy odejmowania?
Wynik odejmowania nazywamy różnicą. Jest to to, co nam zostaje po odjęciu odjemnika od odjemnej. W działaniu 10 - 4 = 6, liczba 6 to różnica. To właśnie ona pokazuje, jaka jest różnica między dwiema liczbami.
Dlaczego w odejmowaniu musisz pilnować kolejności?
W przeciwieństwie do dodawania, odejmowanie nie jest przemienne. Oznacza to, że kolejność liczb ma kluczowe znaczenie i nie można jej dowolnie zmieniać. Na przykład, 8 - 3 = 5, ale już 3 - 8 da nam zupełnie inny wynik (liczbę ujemną, którą poznacie później). Zatem, aby otrzymać poprawną różnicę, musimy zawsze pamiętać o właściwej kolejności odjemnej i odjemnika.
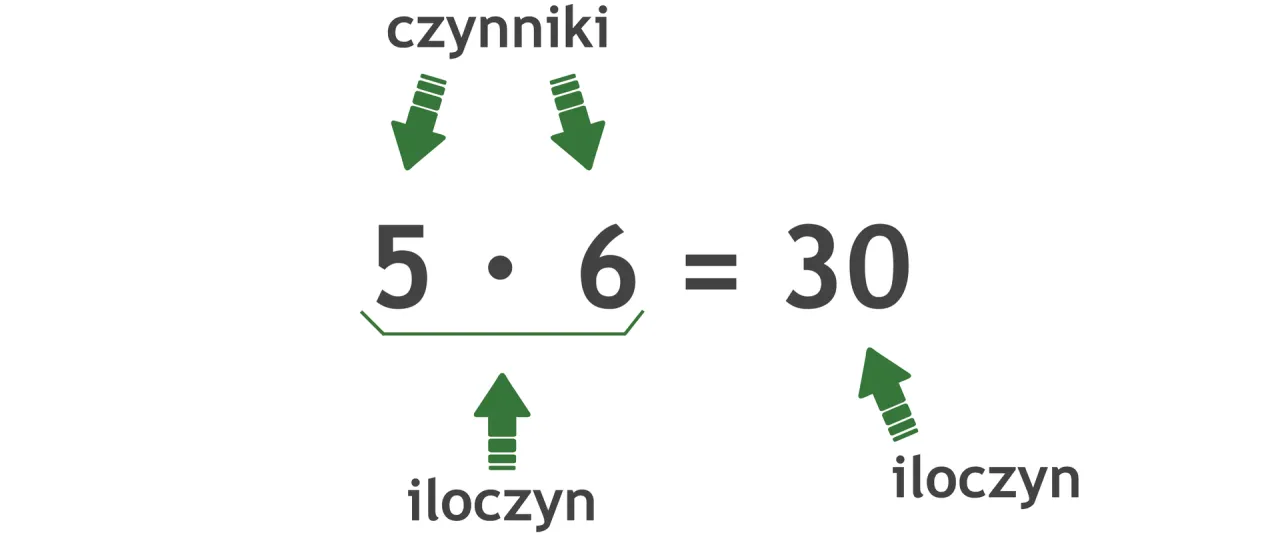
Świat mnożenia: czynniki i iloczyn
Mnożenie to szybki sposób na dodawanie wielu tych samych liczb. Podobnie jak w poprzednich działaniach, ma ono swoje specyficzne nazwy, które pomagają w precyzyjnym opisywaniu operacji.
Czym są czynniki w działaniu mnożenia?
Liczby, które przez siebie mnożymy, nazywamy czynnikami. Są to elementy, które "tworzą" nasz iloczyn. W działaniu 2 × 3 = 6, liczby 2 i 3 są czynnikami. Mogę to porównać do składników w dodawaniu, ale pamiętajmy, że to zupełnie inne działanie i inne nazwy.Iloczyn, czyli co otrzymujemy po pomnożeniu czynników?
Wynik mnożenia to iloczyn. Jest to ostateczny rezultat pomnożenia czynników. W naszym przykładzie 2 × 3 = 6, liczba 6 to iloczyn. To właśnie iloczyn mówi nam, ile razy jedna liczba została "pomnożona" przez drugą.
Czy "składniki mnożenia" to poprawne określenie? Wyjaśniamy wątpliwości
Bardzo często spotykam się z pytaniem, czy można mówić o "składnikach mnożenia". Odpowiedź jest prosta: nie, to błąd. Termin "składnik" odnosi się wyłącznie do dodawania. W mnożeniu używamy wyłącznie określenia czynniki. Pamiętajmy o tej precyzji to właśnie ona odróżnia poprawne rozumienie matematyki od powierzchownego.
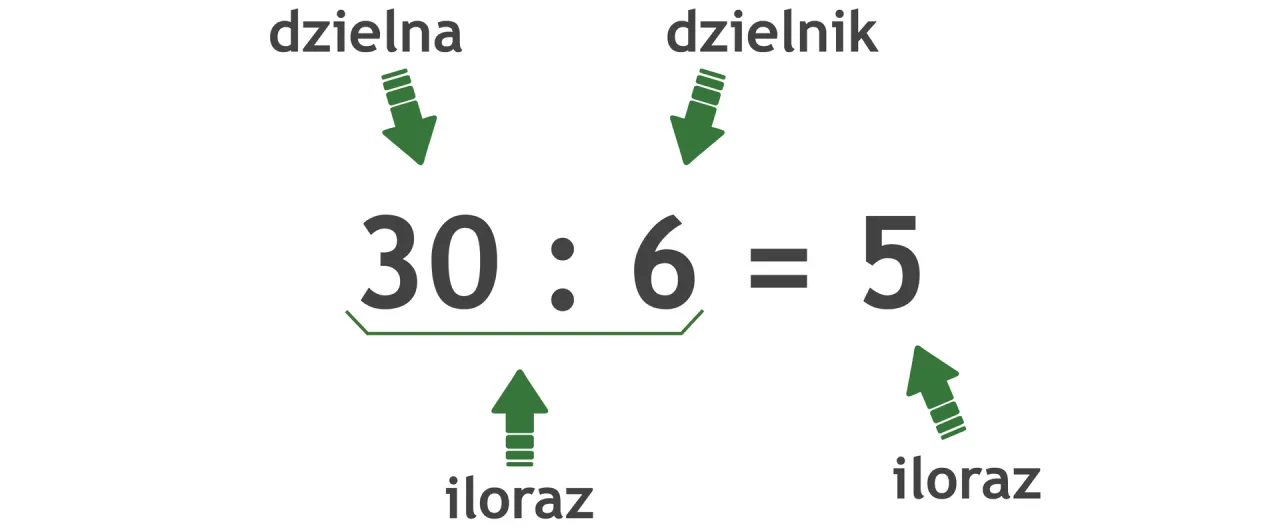
Dzielenie i jego bohaterowie: dzielna, dzielnik oraz iloraz
Dzielenie, będące odwrotnością mnożenia, również ma swoje unikalne nazwy dla poszczególnych elementów. Jest to działanie, które pozwala nam rozdzielać większe ilości na mniejsze, równe części.
Dzielna: Liczba, którą poddajemy dzieleniu
Liczba, którą dzielimy, czyli nasza "całość" do podziału, nazywana jest dzielną. W działaniu 12 : 3 = 4, liczba 12 to dzielna. To właśnie tę liczbę chcemy podzielić na mniejsze części.
Dzielnik: Przez tę liczbę dzielimy
Liczba, przez którą dzielimy dzielną, to dzielnik. Wskazuje on, na ile równych części dzielimy naszą całość. W przykładzie 12 : 3 = 4, liczba 3 to dzielnik. Dzielnik mówi nam, jak duża ma być każda z tych części (lub ile ich ma być).
Iloraz: Wynik, który musisz znać
Wynik dzielenia to iloraz. Jest to odpowiedź na pytanie, ile razy dzielnik mieści się w dzielnej lub ile wynosi każda z równych części. W działaniu 12 : 3 = 4, liczba 4 to iloraz. Iloraz jest kluczowy dla zrozumienia, jak rozłożyły się nasze wartości.
Najważniejsza reguła: Dlaczego nigdy nie wolno dzielić przez zero?
Jest jedna, absolutnie fundamentalna zasada w dzieleniu, której nie wolno łamać: nigdy nie wolno dzielić przez zero. To jest matematycznie niemożliwe i prowadzi do sprzeczności. Wyobraź sobie, że masz 10 ciastek i chcesz je podzielić na 0 osób to po prostu nie ma sensu! Zawsze pamiętajcie, że dzielnik nigdy nie może być zerem.
Dlaczego każde działanie ma inne nazwy? Rola przemienności
Zauważyliście, że każde z czterech podstawowych działań ma swoje unikalne nazwy dla liczb i wyników. To nie przypadek! Ta precyzja języka matematycznego jest niezwykle ważna, a jej korzenie leżą w właściwościach samych działań, zwłaszcza w ich przemienności.
Dodawanie i mnożenie: Działania, gdzie kolejność nie gra roli
Jak już wspomniałem, dodawanie i mnożenie są działaniami przemiennymi. To oznacza, że kolejność liczb nie wpływa na ostateczny wynik. Na przykład, 2 + 3 = 3 + 2 (oba dają 5) oraz 2 × 3 = 3 × 2 (oba dają 6). Dzięki tej właściwości, w tych działaniach możemy swobodnie przestawiać liczby, co często ułatwia nam obliczenia.
Odejmowanie i dzielenie: Tutaj porządek jest kluczowy
Zupełnie inaczej jest w przypadku odejmowania i dzielenia. Te działania nie są przemienne. Zmiana kolejności liczb drastycznie zmienia wynik, a czasem nawet uniemożliwia wykonanie działania w zbiorze liczb naturalnych. Przykładowo, 5 - 2 = 3, ale 2 - 5 to już inna historia. Podobnie, 6 : 2 = 3, ale 2 : 6 to ułamek, a nie liczba całkowita. Dlatego w tych działaniach musimy być szczególnie ostrożni i zawsze pilnować właściwej kolejności liczb.
Przeczytaj również: Jakiego języka się uczyć? Wybierz ten, który zmieni Twoją przyszłość
Kolejność wykonywania działań: Kiedy to jest ważne?
Oprócz znajomości nazw i właściwości działań, niezwykle ważna jest również kolejność wykonywania działań, gdy w jednym wyrażeniu pojawia się ich kilka. Pamiętamy o zasadzie: najpierw działania w nawiasach, potem mnożenie i dzielenie (od lewej do prawej), a na końcu dodawanie i odejmowanie (również od lewej do prawej). Ta hierarchia jest niczym drogowskaz, który pozwala nam unikać błędów i zawsze dochodzić do poprawnego rozwiązania, co jest kolejnym przykładem na to, jak precyzja języka matematycznego jest kluczowa.