W świecie matematyki i nauk ścisłych precyzja jest kluczowa. Znajomość i poprawne rozumienie greckich liter, które stały się nieodłącznym elementem matematycznego języka, jest absolutnie fundamentalne. Ten artykuł to kompleksowy przewodnik, który pomoże zarówno uczniom, studentom, jak i pasjonatom nauk ścisłych zrozumieć i zapamiętać tę bogatą symbolikę, ułatwiając nawigację po złożonych zagadnieniach matematycznych.
Greckie litery w matematyce: Niezbędne symbole i ich kluczowe zastosowania
- Greckie litery uzupełniają alfabet łaciński, umożliwiając precyzyjne oznaczanie stałych, zmiennych i operatorów bez ryzyka pomyłek.
- Stanowią uniwersalny język nauki, ułatwiający globalną komunikację i spójność w matematyce.
- Kluczowe symbole, takie jak Pi (π), Delta (Δ, δ) i Sigma (Σ, σ), mają specyficzne i fundamentalne zastosowania w geometrii, analizie matematycznej i statystyce.
- Artykuł dostarcza kompletny przewodnik po symbolach, od podstawowych (kąty, współczynniki) po zaawansowane (funkcje, wartości własne), wraz z ich znaczeniem.
- Zawiera praktyczne wskazówki dotyczące poprawnej wymowy oraz metod wprowadzania greckich symboli w edytorach tekstu.
Dlaczego matematycy tak chętnie sięgają po alfabet grecki?
Adaptacja alfabetu greckiego w matematyce i naukach ścisłych nie jest przypadkowa, lecz wynika z bardzo praktycznych potrzeb. Głównym powodem jest ograniczona liczba liter w alfabecie łacińskim. W miarę rozwoju matematyki i pojawiania się coraz to nowych pojęć, stałych, zmiennych, funkcji czy operatorów, szybko zabrakłoby unikalnych symboli. Greckie litery pozwoliły na rozszerzenie tego "matematycznego słownictwa", umożliwiając precyzyjne oznaczanie każdego elementu bez ryzyka pomyłek i dwuznaczności.
Co więcej, greckie symbole stały się uniwersalnym językiem nauki. Niezależnie od kraju czy języka ojczystego naukowca, symbol "π" zawsze oznacza stałą Pi, a "Σ" operator sumowania. Taka spójność i jednoznaczność jest kluczowa dla globalnej komunikacji między matematykami i naukowcami, ułatwiając wymianę wiedzy, publikowanie badań i współpracę w międzynarodowym środowisku akademickim. To właśnie dzięki temu mogę dziś swobodnie czytać prace naukowe z każdego zakątka świata, polegając na tej samej, dobrze znanej symbolice.

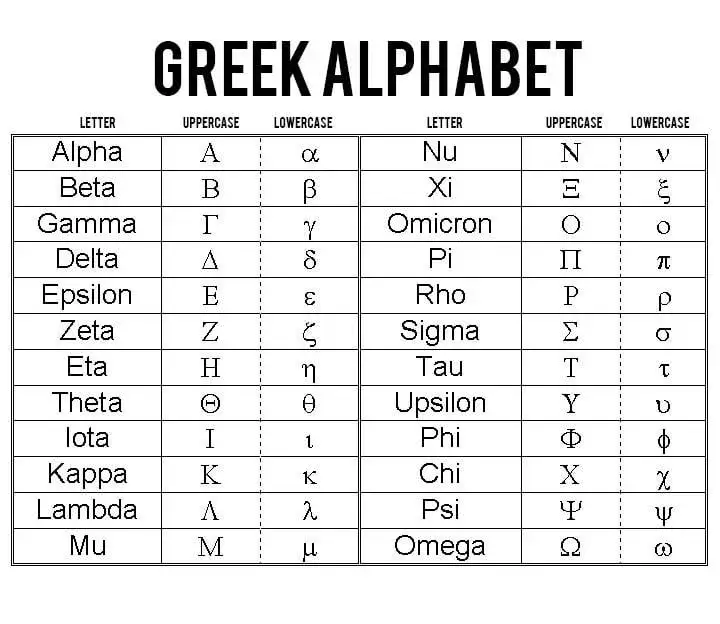
Tabela symboli: Małe i wielkie litery greckie oraz ich podstawowe zastosowania
| Wielka litera | Mała litera | Nazwa | Najczęstsze zastosowania w matematyce |
|---|---|---|---|
| Α | α | Alfa | Oznaczanie kątów, współczynników; w fizyce promieniowanie alfa. |
| Β | β | Beta | Oznaczanie kątów, współczynników w równaniach. |
| Γ | γ | Gamma | Kąty; w matematyce wyższej funkcja gamma Eulera; w fizyce promieniowanie gamma, fotony. |
| Δ | δ | Delta | Δ: zmiana/przyrost wartości (np. Δx), wyróżnik równania kwadratowego. δ: w analizie matematycznej (definicja granicy), symbol delty Kroneckera. |
| Ε | ε | Epsilon | Bardzo mała, dodatnia liczba w analizie matematycznej (definicja granicy). |
| Ζ | ζ | Dzeta | Głównie w funkcji dzeta Riemanna w teorii liczb. |
| Η | η | Eta | Często używana w fizyce do oznaczania efektywności lub współczynników. |
| Θ | θ | Theta | Popularne oznaczenie miary kąta, zwłaszcza we współrzędnych biegunowych. |
| Ι | ι | Jota | Rzadziej używana, czasami jako indeks lub zmienna. |
| Κ | κ | Kappa | Współczynniki, krzywizna. |
| Λ | λ | Lambda | Wartości własne w algebrze liniowej; w fizyce długość fali. |
| Μ | μ | Mi | Średnia arytmetyczna w statystyce (wartość oczekiwana); w fizyce współczynnik tarcia. |
| Ν | ν | Ni | W fizyce częstotliwość fali. |
| Ξ | ξ | Ksi | Zmienna losowa w rachunku prawdopodobieństwa. |
| Ο | ο | Omikron | Rzadko używana, ze względu na podobieństwo do łacińskiej litery 'o'. |
| Π | π | Pi | π: stała matematyczna (ok. 3,14159). Π: operator iloczynu. |
| Ρ | ρ | Rho | W fizyce gęstość; w statystyce współczynnik korelacji. |
| Σ | σ | Sigma | Σ: operator sumowania. σ: odchylenie standardowe w statystyce. |
| Τ | τ | Tau | Moment siły; w statystyce współczynnik korelacji rangowej Kendalla. |
| Υ | υ | Ypsilon | Rzadziej używana, czasami jako zmienna. |
| Φ | φ | Fi/Phi | Złota proporcja (liczba Fibonacciego); funkcja w teorii liczb; oznaczanie kątów. |
| Χ | χ | Chi | Rozkład chi-kwadrat w statystyce. |
| Ψ | ψ | Psi | Funkcja falowa w mechanice kwantowej. |
| Ω | ω | Omega | Ω: om (jednostka oporu elektrycznego), zbiór wszystkich zdarzeń elementarnych. ω: prędkość kątowa, częstość kołowa. |
Jak poprawnie czytać i wymawiać greckie nazwy liter?
Poprawna wymowa greckich liter jest ważna, aby móc swobodnie komunikować się w środowisku naukowym. Wiele z nich wymawia się intuicyjnie, zgodnie z polskimi zasadami, ale są też pewne niuanse. Na przykład, Pi wymawiamy jako "pi", Sigma jako "sigma" (z akcentem na 'i'), a Delta jako "delta". Warto zwrócić uwagę na Epsilon, które wymawiamy jako "epsilon", czy Lambda jako "lambda". Często spotykane Fi wymawia się jako "fi" lub "phi", a Omega jako "omega". Generalnie, polska fonetyka dobrze oddaje brzmienie większości tych symboli, co ułatwia ich przyswajanie.
Pi (π): Znacznie więcej niż tylko 3,14 serce geometrii i analizy
Mała litera Pi (π) to bez wątpienia jedna z najbardziej rozpoznawalnych stałych matematycznych. Jej wartość, w przybliżeniu 3,14159, reprezentuje stosunek obwodu koła do jego średnicy. Jest to fundamentalna liczba w geometrii, pojawiająca się we wzorach na obwód (2πr) i pole koła (πr²), a także w objętościach i powierzchniach wielu brył obrotowych. Jednak jej znaczenie wykracza daleko poza geometrię; Pi jest wszechobecne w analizie matematycznej, trygonometrii, rachunku prawdopodobieństwa i wielu innych dziedzinach. Z kolei wielka litera Pi (Π) pełni rolę operatora iloczynu, analogicznego do operatora sumowania Sigma (Σ). Jeśli mamy ciąg liczb a₁, a₂, ..., aₙ, to Πᵢ=₁ⁿ aᵢ oznacza iloczyn wszystkich tych liczb: a₁ * a₂ * ... * aₙ.
Delta (Δ, δ): Symbol zmiany, wyboru i precyzji w matematyce
Litera Delta, zarówno w formie wielkiej (Δ), jak i małej (δ), ma szerokie zastosowania w matematyce. Wielka Delta (Δ) najczęściej symbolizuje zmianę lub przyrost wartości, na przykład Δx oznacza zmianę wartości zmiennej x. Jest to kluczowe w rachunku różniczkowym, gdzie Δx dąży do zera. Ponadto, Δ jest powszechnie używana jako wyróżnik (dyskryminanta) równania kwadratowego (Δ = b² - 4ac), decydując o liczbie jego rozwiązań. Mała Delta (δ) odgrywa z kolei fundamentalną rolę w analizie matematycznej, szczególnie w formalnej definicji granicy ciągu i funkcji, gdzie δ oznacza bardzo małą, dodatnią liczbę, związaną z odległością na osi x. Używana jest również jako symbol delty Kroneckera, która przyjmuje wartość 1, gdy indeksy są równe, i 0 w przeciwnym razie.
Sigma (Σ, σ): Potęga sumowania i klucz do zrozumienia statystyki
Sigma to kolejna litera greckiego alfabetu o ogromnym znaczeniu w matematyce. Wielka litera Sigma (Σ) jest powszechnie rozpoznawana jako operator sumowania. Używamy jej, aby w skrócony sposób zapisać sumę wielu składników. Na przykład, Σᵢ=₁ⁿ aᵢ oznacza sumę a₁ + a₂ + ... + aₙ. Jest to niezastąpione narzędzie w algebrze, analizie, statystyce i wielu innych dziedzinach, pozwalające na zwięzłe przedstawianie skomplikowanych wyrażeń. Mała litera Sigma (σ) jest natomiast kluczowym symbolem w statystyce, gdzie oznacza odchylenie standardowe. Odchylenie standardowe mierzy rozrzut danych wokół średniej, co jest fundamentalne dla zrozumienia zmienności i precyzji w analizie danych. To właśnie dzięki σ możemy ocenić, jak bardzo poszczególne wartości odbiegają od średniej w danym zbiorze.
Alfa (α), Beta (β), Gamma (γ): Nie tylko kąty fundamenty trygonometrii
Litery Alfa (α), Beta (β) i Gamma (γ) są jednymi z pierwszych greckich symboli, z którymi spotykamy się w edukacji matematycznej, zwłaszcza w geometrii i trygonometrii. Ich najbardziej powszechne zastosowanie to oznaczanie kątów w trójkątach, figurach geometrycznych czy w układach współrzędnych. Poza tym, α i β często służą jako ogólne współczynniki w równaniach liniowych lub kwadratowych, a także jako parametry w różnych modelach matematycznych. Gamma (γ) ma również swoje specyficzne zastosowania, takie jak funkcja gamma Eulera w analizie matematycznej, która jest uogólnieniem silni na liczby rzeczywiste i zespolone. W fizyce, te same litery oznaczają również rodzaje promieniowania: alfa, beta i gamma, co pokazuje interdyscyplinarny charakter greckiej symboliki.
Lambda (λ) i Omega (Ω, ω): Od algebry liniowej po rachunek prawdopodobieństwa
Lambda (λ) to litera o szczególnym znaczeniu w algebrze liniowej, gdzie jest powszechnie używana do oznaczania wartości własnych macierzy. Wartości własne są kluczowe dla zrozumienia transformacji liniowych i diagonalizacji macierzy. W fizyce, λ symbolizuje długość fali, co jest fundamentalne w optyce i mechanice kwantowej. Z kolei Omega (Ω) i omega (ω) mają różnorodne zastosowania. Wielka litera Omega (Ω) jest standardowym symbolem dla oma, jednostki oporu elektrycznego w fizyce. W rachunku prawdopodobieństwa Ω często oznacza zbiór wszystkich zdarzeń elementarnych w danym eksperymencie. Mała litera omega (ω) jest używana do oznaczania prędkości kątowej w fizyce (np. w ruchu obrotowym) lub częstości kołowej w analizie sygnałów, co podkreśla jej rolę w opisie zjawisk cyklicznych.
Epsilon (ε) i jego rola w definiowaniu granic ciągów i funkcji
Epsilon (ε) to litera, która nabiera kluczowego znaczenia w zaawansowanej analizie matematycznej, szczególnie przy formalnym definiowaniu granic ciągów i funkcji. Jest to symbol, który zawsze oznacza bardzo małą, dodatnią liczbę. W definicji granicy, na przykład, mówimy, że funkcja f(x) ma granicę L, jeśli dla każdego ε > 0 istnieje takie δ > 0, że... Epsilon pozwala nam precyzyjnie określić, jak blisko wartości funkcji muszą być do granicy L. Jego obecność w tych definicjach jest fundamentalna, ponieważ umożliwia ścisłe i jednoznaczne formułowanie pojęć takich jak ciągłość, zbieżność czy różniczkowalność, stanowiąc kamień węgielny rachunku różniczkowego i całkowego.
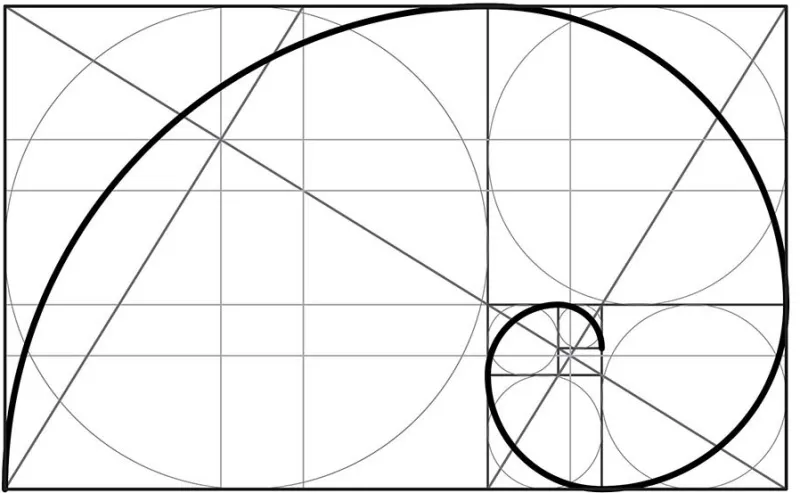
Fi (φ): Złota proporcja ukryta w naturze i matematyce
Litera Fi (φ), często wymawiana jako "fi" lub "phi", jest nierozerwalnie związana z koncepcją złotej proporcji, znanej również jako złota liczba (w przybliżeniu 1.618). Ta irracjonalna stała matematyczna fascynuje naukowców i artystów od wieków ze względu na jej niezwykłe właściwości estetyczne i częste występowanie w naturze (np. w spiralach muszli, układzie liści) oraz w sztuce i architekturze. W matematyce, φ pojawia się w ciągu Fibonacciego i ma głębokie powiązania z geometrią. Poza złotą proporcją, Fi może być również używane do oznaczania kątów, podobnie jak Alfa czy Beta, a także jako symbol funkcji w teorii liczb (np. funkcja Eulera φ(n)).
Rho (ρ) i Mi (μ): Kluczowe wskaźniki w świecie statystyki
Rho (ρ) i Mi (μ) to kolejne greckie litery, które odgrywają istotne role w matematyce i fizyce. Rho (ρ) jest powszechnie używane w fizyce do oznaczania gęstości materiału, co jest kluczowe w mechanice płynów i termodynamice. W statystyce, ρ symbolizuje współczynnik korelacji populacji, mierząc siłę i kierunek liniowego związku między dwiema zmiennymi. Z kolei Mi (μ) jest jednym z najważniejszych symboli w statystyce, gdzie oznacza średnią arytmetyczną populacji (wartość oczekiwaną). Jest to podstawowy parametr opisujący centralną tendencję zbioru danych. W fizyce, μ często reprezentuje współczynnik tarcia, co jest kluczowe w mechanice klasycznej.
Najczęstsze pomyłki i jak ich unikać (np. ν vs v, ρ vs p)
Chociaż greckie litery wzbogacają symbolikę matematyczną, ich podobieństwo do niektórych liter łacińskich może prowadzić do pomyłek, szczególnie w piśmie ręcznym. Jednym z klasycznych przykładów jest litera Ni (ν), która często bywa mylona z łacińskim "v". Inna częsta pomyłka to Rho (ρ), które łatwo pomylić z łacińskim "p". Aby uniknąć takich nieporozumień, zawsze staram się pisać greckie litery wyraźnie, zwracając uwagę na ich charakterystyczne cechy (np. ogonek w ν, bardziej zaokrąglona pętla w ρ). W edytorach tekstu problem ten jest mniejszy, ponieważ symbole są precyzyjnie renderowane, ale w notatkach odręcznych warto być szczególnie ostrożnym, aby zapewnić klarowność matematycznych zapisów.
Skróty klawiaturowe i kody Alt: Sposoby na szybkie wstawianie symboli w edytorach tekstu
W dobie edukacji cyfrowej i pracy z dokumentami elektronicznymi, umiejętność szybkiego wstawiania greckich symboli w edytorach tekstu jest niezwykle przydatna. To częste wyzwanie, z którym borykają się studenci i naukowcy. W programach takich jak Microsoft Word, można skorzystać z funkcji "Wstaw symbol" (Insert Symbol), gdzie znajdziemy pełen zestaw greckich liter. Alternatywnie, dla wielu symboli istnieją kody Alt (np. Alt + 227 dla π, Alt + 931 dla Σ), które można wpisać, trzymając klawisz Alt i używając klawiatury numerycznej. W środowisku LaTeX, które jest standardem w publikacjach naukowych, greckie litery wprowadza się za pomocą prostych komend, np. `\pi` dla π, `\Sigma` dla Σ, `\alpha` dla α. Istnieją również dodatki do przeglądarek i programów, które ułatwiają wprowadzanie tych symboli, co znacznie przyspiesza pracę.
Krótka wzmianka o alfabecie hebrajskim (np. alef w teorii mnogości)
Chociaż alfabet grecki dominuje w symbolice matematycznej, warto wspomnieć, że matematyka czerpie inspirację również z innych alfabetów. Doskonałym przykładem jest hebrajska litera Alef (ℵ), która znalazła swoje stałe miejsce w teorii mnogości. Jest ona używana do oznaczania mocy zbiorów nieskończonych, czyli "rozmiaru" nieskończoności. Na przykład ℵ₀ (alef zero) oznacza moc zbioru liczb naturalnych, a ℵ₁ (alef jeden) moc kolejnego, większego zbioru nieskończonego. Pokazuje to, że choć rzadsze, inne alfabety również wzbogacają symbolikę matematyczną, pozwalając na precyzyjne nazywanie i rozróżnianie złożonych pojęć.
Przeczytaj również: Konwersja równania prostej: Kierunkowa na ogólną krok po kroku
Dlaczego konsekwentne stosowanie symboliki jest kluczem do sukcesu?
Na koniec chciałbym podkreślić, że konsekwentne i precyzyjne stosowanie symboliki matematycznej, w tym greckich liter, jest absolutnie kluczowe dla sukcesu w każdej dziedzinie nauki. To nie jest jedynie kwestia estetyki czy tradycji, ale przede wszystkim jasności, jednoznaczności i efektywnej komunikacji. Poprawne użycie symboli minimalizuje ryzyko błędów interpretacyjnych, ułatwia zrozumienie skomplikowanych koncepcji i pozwala na swobodną wymianę myśli w międzynarodowym środowisku naukowym. Dla każdego, kto pracuje z matematyką, czy to w szkole, na studiach, czy w pracy zawodowej, opanowanie tej symboliki jest fundamentem, na którym buduje się dalszą wiedzę i umiejętności.