Czy zastanawiałeś się kiedyś, jak sprawdzić, czy konkretna liczba jest "rozwiązaniem" równania? W tym artykule skupimy się na jednej z najbardziej fascynujących liczb zerze. Pokażę Ci, krok po kroku, jak zweryfikować, czy zero spełnia dane równanie. To praktyczny przewodnik, który pomoże Ci zrozumieć podstawy algebry i uniknąć typowych błędów. Przygotuj się na to, że matematyka stanie się dla Ciebie prostsza i bardziej intuicyjna!
Zero spełnia równanie, gdy po podstawieniu go za niewiadomą lewa strona równa się prawej sprawdź, jak to zrobić krok po kroku.
- Liczba spełnia równanie, jeśli po podstawieniu jej w miejsce niewiadomej, lewa strona równania jest równa prawej.
- Aby sprawdzić, czy zero spełnia równanie, należy podstawić 0 w miejsce niewiadomej, wykonać obliczenia po obu stronach i porównać wyniki.
- Kluczowe właściwości zera to: każda liczba pomnożona przez 0 daje 0, dodanie/odjęcie 0 nie zmienia wartości, a 0 podniesione do dodatniej potęgi daje 0.
- Zwróć uwagę na kolejność działań, znaki przy liczbach ujemnych i poprawną interpretację wyniku, aby uniknąć typowych błędów.
Co to znaczy, że liczba spełnia równanie?
Kiedy mówimy, że liczba spełnia równanie, mamy na myśli, że po podstawieniu tej liczby w miejsce niewiadomej (najczęściej oznaczanej jako x, y lub z) i wykonaniu wszystkich działań, lewa strona równania staje się równa prawej. Innymi słowy, po podstawieniu otrzymujemy prawdziwą równość, na przykład 5 = 5. Taka liczba jest nazywana rozwiązaniem lub pierwiastkiem równania. To fundamentalna zasada, którą musimy opanować, zanim przejdziemy do konkretów z zerem.
Zero to naprawdę wyjątkowa liczba w matematyce, a jej unikalne właściwości sprawiają, że sprawdzanie równań z jej udziałem jest często znacznie prostsze. Pomyśl tylko: mnożenie przez zero zawsze daje zero, dodawanie czy odejmowanie zera nie zmienia wartości, a zero podniesione do dodatniej potęgi to nadal zero. Te "magiczne" cechy zera są naszymi sprzymierzeńcami i znacznie ułatwiają obliczenia, co zaraz pokażę na przykładach.
Zadania polegające na sprawdzaniu, czy dana liczba spełnia równanie, są kluczowym elementem nauczania podstaw algebry, zwłaszcza w klasach 6-7 szkoły podstawowej. Ich celem jest nie tylko utrwalenie pojęcia rozwiązania równania, ale także przećwiczenie podstawowych operacji arytmetycznych w praktycznym kontekście. To solidny fundament do dalszej, bardziej zaawansowanej nauki matematyki.
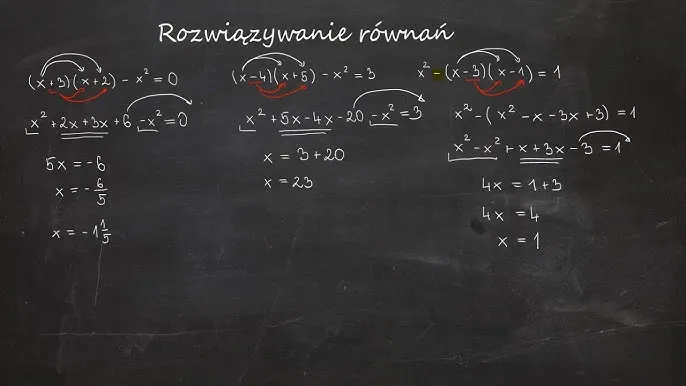
Jak sprawdzić, czy zero jest rozwiązaniem równania przewodnik krok po kroku
Pierwszym i absolutnie najważniejszym krokiem w weryfikacji, czy zero jest rozwiązaniem równania, jest wstawienie liczby 0 w każde miejsce, gdzie występuje niewiadoma. Niezależnie od tego, czy jest to x, y, czy z, po prostu zastąp ją zerem. To klucz do dalszych obliczeń i podstawa całego procesu bez tego ani rusz!
Po podstawieniu zera w miejsce niewiadomej, czas na wykonanie wszystkich działań, oddzielnie po lewej i prawej stronie równania. Pamiętaj o prawidłowej kolejności wykonywania działań, która jest niezmienna i kluczowa dla uzyskania poprawnego wyniku:
- Nawiasy
- Potęgowanie
- Mnożenie/Dzielenie (w kolejności występowania od lewej do prawej)
- Dodawanie/Odejmowanie (w kolejności występowania od lewej do prawej)
Dopiero po wykonaniu wszystkich obliczeń po obu stronach równania, możesz przejść do ostatniego kroku: porównania uzyskanych wyników. Jeśli liczba po lewej stronie jest identyczna z liczbą po prawej stronie, oznacza to, że zero spełnia to równanie. Jeśli wyniki są różne, na przykład po lewej stronie wyszło 5, a po prawej 7, to zero nie jest rozwiązaniem danego równania. To proste równość musi być prawdziwa!

Przykłady, które rozwieją wszelkie wątpliwości
Przyjrzyjmy się równaniu: 3x + 5 = 5.
Krok 1: Podstawiamy 0 za x.
3 * 0 + 5 = 5
Krok 2: Wykonujemy obliczenia. Pamiętamy, że 3 * 0 = 0.
0 + 5 = 5
5 = 5
Krok 3: Porównujemy wyniki. Lewa strona jest równa prawej.
Wniosek: Liczba 0 spełnia to równanie.
Teraz przykład z niewiadomą po obu stronach: 2 - 3x = 5x + 2.
Krok 1: Podstawiamy 0 za x po obu stronach.
2 - 3 * 0 = 5 * 0 + 2
Krok 2: Wykonujemy obliczenia. Pamiętamy, że 3 * 0 = 0 i 5 * 0 = 0.
2 - 0 = 0 + 2
2 = 2
Krok 3: Porównujemy wyniki. Lewa strona jest równa prawej.
Wniosek: Liczba 0 spełnia to równanie.
A co z równaniami z nawiasami i potęgami? Sprawdźmy: x(x + 2) = 0.
Krok 1: Podstawiamy 0 za x.
0 * (0 + 2) = 0
Krok 2: Wykonujemy obliczenia. Najpierw nawias: 0 + 2 = 2. Następnie mnożenie: 0 * 2 = 0.
0 = 0
Krok 3: Porównujemy wyniki. Lewa strona jest równa prawej.
Wniosek: Liczba 0 spełnia to równanie. Jak widzisz, właściwość mnożenia przez zero bardzo tu pomogła!
Na koniec przykład, którego zero nie spełnia: x + 5 = 7.
Krok 1: Podstawiamy 0 za x.
0 + 5 = 7
Krok 2: Wykonujemy obliczenia.
5 = 7
Krok 3: Porównujemy wyniki. Lewa strona (5) nie jest równa prawej (7).
Wniosek: Liczba 0 nie spełnia tego równania. To ważne, aby umieć poprawnie zinterpretować wynik, gdy równość nie jest prawdziwa.
Magiczne właściwości zera Twoi sprzymierzeńcy w równaniach
Jedną z najbardziej przydatnych właściwości zera jest to, że każda liczba pomnożona przez zero daje zero. To ogromne ułatwienie przy sprawdzaniu równań! Niezależnie od tego, czy masz 5 * 0 = 0, -10 * 0 = 0, czy nawet (a + b) * 0 = 0, wynik zawsze będzie zero. Ta zasada upraszcza wiele skomplikowanych wyrażeń do zera, co znacznie przyspiesza obliczenia.
Kolejną "magiczną" cechą zera jest to, że dodanie lub odjęcie zera nie zmienia wartości liczby. Jeśli masz 7 + 0, wynik to 7. Podobnie, 7 - 0 to również 7. To oznacza, że możesz po prostu "zignorować" zera, które są dodawane lub odejmowane w równaniu, co jeszcze bardziej upraszcza rachunki.
W kontekście potęgowania, zero również jest wyjątkowe: zero podniesione do dowolnej dodatniej potęgi daje zero. Czyli 0^2 = 0, 0^5 = 0, a nawet 0^100 = 0. Warto też wspomnieć, że zero podzielone przez dowolną liczbę różną od zera daje wynik 0 (np. 0 / 5 = 0). Pamiętaj jednak, że dzielenie przez zero jest niewykonalne nigdy nie możesz dzielić przez zero!

Unikaj pułapek najczęstsze błędy i jak sobie z nimi radzić
Nawet jeśli znasz właściwości zera, łatwo jest popełnić błąd, jeśli zapomnisz o prawidłowej kolejności wykonywania działań. Zawsze najpierw nawiasy, potem potęgi, następnie mnożenie i dzielenie, a na końcu dodawanie i odejmowanie. Na przykład, w wyrażeniu2 + 3 * 0, jeśli najpierw dodasz (2+3=5), a potem pomnożysz przez 0, otrzymasz 0. Poprawnie jest najpierw pomnożyć (3*0=0), a potem dodać (2+0=2). Różnica jest kolosalna! Inną pułapką są błędy w operacjach na liczbach ujemnych. Jeśli w równaniu pojawiają się liczby ujemne, na przykład -2x + 5 = 5, po podstawieniu zera mamy -2 * 0 + 5 = 5, co daje 0 + 5 = 5, a więc 5 = 5. Zero spełnia to równanie. Jednak w bardziej złożonych przypadkach, zwłaszcza przy odejmowaniu liczb ujemnych, łatwo o pomyłkę. Zawsze bądź ostrożny ze znakami!
Ostatni, ale równie ważny błąd, to nieprawidłowa interpretacja wyniku. Jeśli po wszystkich obliczeniach otrzymasz na przykład 3 = 5, to musisz jasno stwierdzić, że sprawdzana liczba (w tym przypadku zero) nie spełnia danego równania. Nie próbuj "dopasowywać" wyniku, aby pasował do oczekiwań. Matematyka jest precyzyjna i jeśli lewa strona nie równa się prawej, to równanie nie jest spełnione.
Przeczytaj również: Dzielna i dzielnik: Jak je odróżnić? Proste triki i przykłady!
Podsumowanie: Twoja nowa superumiejętność w matematyce
Właśnie zdobyłeś nową, ważną superumiejętność w matematyce! Oto trzy kluczowe kroki, które pozwolą Ci bezbłędnie sprawdzić, czy zero spełnia równanie:
- Podstaw 0 w miejsce każdej niewiadomej w równaniu.
- Wykonaj obliczenia po obu stronach równania, pamiętając o prawidłowej kolejności działań.
- Porównaj wyniki: jeśli lewa strona równa się prawej, zero spełnia równanie; w przeciwnym razie nie.
Ta umiejętność to fundament, na którym zbudujesz swoją wiedzę z algebry. Zrozumienie, jak weryfikować rozwiązania równań, pozwoli Ci pewniej podchodzić do bardziej złożonych problemów matematycznych i otworzy drzwi do dalszego, fascynującego świata liczb i niewiadomych. Ćwicz, a zobaczysz, jak szybko staniesz się prawdziwym ekspertem!

