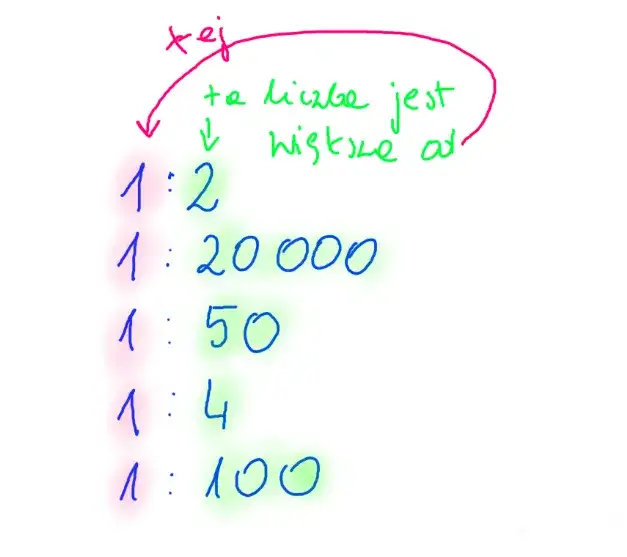Skala w matematyce: Opanuj obliczenia i unikaj pułapek!

Skala w matematyce to fascynujące narzędzie, które pozwala nam przedstawiać ogromne przestrzenie lub bardzo małe obiekty w sposób zrozumiały i użyteczny. Dzięki niej możemy bez trudu odczytywać odległości z mapy, planować rozmieszczenie mebli w mieszkaniu czy budować modele samolotów. W tym artykule, jako Alan Szymczak, pokażę Ci krok po kroku, czym jest skala, jakie są jej rodzaje i co najważniejsze jak bezbłędnie rozwiązywać zadania, które często sprawiają trudność.

Skala bez tajemnic: definicja, którą zrozumie każdy

Zacznijmy od podstaw. Czym właściwie jest skala? Najprościej mówiąc, skala to informacja o tym, ile razy coś zostało pomniejszone lub powiększone, aby zmieściło się na kartce papieru, ekranie czy w formie modelu. To stosunek długości na rysunku (mapie, planie) do rzeczywistej długości w terenie. Dzięki niej wiemy, że każdy centymetr na mapie odpowiada konkretnej liczbie centymetrów, metrów czy kilometrów w realnym świecie.

Skala w matematyce to stosunek wielkości liniowej (długości) obiektu lub odległości przedstawionej na mapie, planie, rysunku technicznym lub w modelu do odpowiadającej jej wielkości w rzeczywistości.

Od mapy do modelu samolotu: gdzie w codziennym życiu ukrywa się skala?

Skala to nie tylko szkolna abstrakcja. Otacza nas każdego dnia! Kiedy korzystasz z Google Maps lub nawigacji GPS w samochodzie, skala jest kluczowa to ona pozwala Ci zobaczyć, jak daleko masz do celu i jak duży obszar obejmuje widok na ekranie. Architekci i inżynierowie używają skali do tworzenia planów budynków, mostów czy maszyn, dzięki czemu wszystko jest proporcjonalne i precyzyjne. Modelarze, budując miniaturowe repliki samolotów, statków czy samochodów, również muszą ściśle trzymać się skali, aby ich dzieła były wiernym odzwierciedleniem oryginału. Nawet w kuchni, gdy zmniejszasz lub zwiększasz przepis, aby ugotować obiad dla mniejszej lub większej liczby osób, tak naprawdę operujesz skalą, czyli proporcjami składników.

Trzy oblicza skali: którą z nich musisz znać, by rozwiązać zadanie?

Aby skutecznie pracować ze skalą, musimy poznać jej różne formy. W zależności od tego, czy patrzymy na mapę, plan czy rysunek techniczny, możemy spotkać się z trzema głównymi rodzajami skali. Każda z nich przekazuje tę samą informację, ale w nieco inny sposób.

Skala liczbowa (np. 1: 100) jak ją poprawnie odczytać?

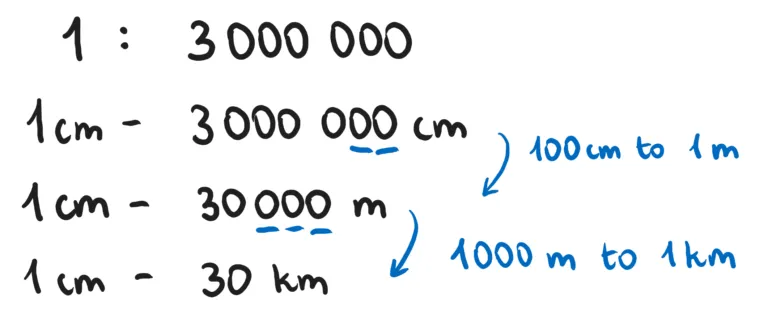
Skala liczbowa to najbardziej uniwersalny sposób zapisu skali. Zawsze przedstawia się ją jako stosunek dwóch liczb, np. 1:100, 1:10 000, 1:2 000 000. Pierwsza liczba (zazwyczaj 1) oznacza długość na mapie lub planie, a druga liczba oznacza odpowiadającą jej długość w rzeczywistości, zawsze w tych samych jednostkach. Na przykład, skala 1:100 000 oznacza, że 1 centymetr na mapie to 100 000 centymetrów w rzeczywistości. Aby to sobie lepiej wyobrazić, warto od razu przeliczyć te centymetry na bardziej zrozumiałe jednostki. 100 000 cm to 1000 metrów, czyli 1 kilometr. Zatem 1 cm na mapie w skali 1:100 000 to 1 km w terenie.

Skala mianowana (np. 1 cm -> 1 km) praktyczny skrót myślowy

Skala mianowana to nic innego jak skala liczbowa, która została już przetłumaczona na bardziej praktyczny język. Zapisuje się ją w formie, która od razu mówi nam, ile wynosi 1 cm na mapie w rzeczywistości, ale z podanymi jednostkami. Przykładem jest 1 cm -> 1 km. Taki zapis jest bardzo wygodny, ponieważ od razu widzimy, że jeden centymetr na mapie odpowiada jednemu kilometrowi w terenie. Nie musimy nic przeliczać, co znacznie ułatwia szybkie szacowanie odległości. Jest to po prostu skala liczbowa 1:100 000, ale przedstawiona w bardziej intuicyjny sposób.

Podziałka liniowa graficzny przewodnik po odległościach

Podziałka liniowa to graficzne przedstawienie skali, często spotykane na mapach. Jest to po prostu odcinek podzielony na mniejsze części, z zaznaczonymi wartościami odpowiadającymi rzeczywistym odległościom. Na przykład, na podziałce może być zaznaczone, że odcinek o długości 2 cm na mapie odpowiada 1 km w rzeczywistości. Jej wielką zaletą jest to, że działa niezależnie od tego, czy mapa jest powiększana, czy pomniejszana (np. podczas kopiowania). W przeciwieństwie do skali liczbowej, która staje się nieprawidłowa po zmianie rozmiaru mapy, podziałka liniowa "rozciąga się" lub "kurczy" wraz z mapą, zachowując swoją poprawność. Aby z niej skorzystać, wystarczy zmierzyć odległość na mapie linijką, a następnie przyłożyć linijkę do podziałki, aby odczytać rzeczywistą wartość.

Klucz do sukcesu: jak bezbłędnie przeliczać jednostki w zadaniach ze skalą?

Z mojego doświadczenia wiem, że największym wyzwaniem w zadaniach ze skalą nie jest sama skala, ale umiejętne przeliczanie jednostek długości. Bez tej umiejętności łatwo o błędy. Dlatego poświęćmy temu chwilę uwagi.

Zamiana kilometrów na centymetry w 3 prostych krokach

Często w zadaniach musimy przeliczyć kilometry na centymetry, aby móc porównać je ze skalą liczbową. Oto jak to zrobić:

1. Krok 1: Zamień kilometry na metry.
   • Pamiętaj, że 1 kilometr (km) to 1000 metrów (m).
   • Przykład: Jeśli masz 5 km, to 5 km * 1000 m/km = 5000 m.
2. Krok 2: Zamień metry na centymetry.
   • Pamiętaj, że 1 metr (m) to 100 centymetrów (cm).
   • Przykład: Jeśli masz 5000 m, to 5000 m * 100 cm/m = 500 000 cm.
3. Krok 3: Połącz kroki zamień kilometry od razu na centymetry.
   • Jeśli 1 km = 1000 m, a 1 m = 100 cm, to 1 km = 1000 * 100 cm = 100 000 cm.
   • Przykład: Jeśli masz 5 km, to 5 km * 100 000 cm/km = 500 000 cm.

Widzisz? To wcale nie jest takie trudne, jeśli znasz podstawowe przeliczniki!

Pamiętaj o tym, a już nigdy nie pomylisz metrów z milimetrami

Aby uniknąć najczęstszych błędów przy przeliczaniu jednostek, mam dla Ciebie kilka wskazówek:

• Zawsze zapisuj jednostki: Przy każdym kroku obliczeń zapisuj, czy to centymetry, metry czy kilometry. To pomaga utrzymać porządek.
• Pamiętaj o zerach: Przy zamianie km na cm, dodajesz aż pięć zer (1 km = 100 000 cm). To kluczowe!
• Używaj skali mianowanej jako "ściągawki": Jeśli skala liczbowa to 1:50 000, od razu przelicz to na skalę mianowaną: 1 cm -> 50 000 cm, czyli 1 cm -> 500 m. To ułatwi dalsze obliczenia.
• Ćwicz, ćwicz, ćwicz: Im więcej razy przeliczysz jednostki, tym szybciej i pewniej będziesz to robić.

Rozwiązywanie zadań ze skalą krok po kroku: praktyczny poradnik

Teraz, gdy już rozumiemy, czym jest skala i jak przeliczać jednostki, przejdźmy do sedna rozwiązywania typowych zadań. Przygotowałem dla Ciebie instrukcje krok po kroku dla trzech najczęściej spotykanych typów zadań ze skalą.

Zadanie typ 1: Jak obliczyć rzeczywistą odległość, znając skalę i wymiar na mapie?

To najczęstszy typ zadania. Musimy dowiedzieć się, jaka jest prawdziwa odległość w terenie.

1. Krok 1: Przeczytaj skalę i zapisz ją w formie mianowanej.
   • Przykład: Skala mapy to 1:200 000. Oznacza to, że 1 cm na mapie to 200 000 cm w rzeczywistości.
   • Przelicz na metry/kilometry: 200 000 cm = 2000 m = 2 km. Zatem skala mianowana to 1 cm -> 2 km.
2. Krok 2: Zmierz odległość na mapie (lub odczytaj z treści zadania).
   • Przykład: Odległość między dwoma miastami na mapie wynosi 7 cm.
3. Krok 3: Oblicz rzeczywistą odległość.
   • Pomnóż odległość na mapie przez wartość, którą reprezentuje 1 cm w rzeczywistości (ze skali mianowanej).
   • Przykład: 7 cm * 2 km/cm = 14 km.
   • Rzeczywista odległość między miastami to 14 km.

Zadanie typ 2: Jak obliczyć wymiar na planie, znając rzeczywistą odległość i skalę?

Tutaj musimy dowiedzieć się, jaką długość będzie miał dany obiekt na mapie lub planie.

1. Krok 1: Przeczytaj skalę i zapisz ją w formie mianowanej.
   • Przykład: Skala planu to 1:500. Oznacza to, że 1 cm na planie to 500 cm w rzeczywistości.
   • Przelicz na metry: 500 cm = 5 m. Zatem skala mianowana to 1 cm -> 5 m.
2. Krok 2: Zapisz rzeczywistą odległość i przelicz ją na jednostki zgodne ze skalą.
   • Przykład: Rzeczywista długość pokoju to 6 metrów.
   • Przelicz na centymetry: 6 m * 100 cm/m = 600 cm.
3. Krok 3: Oblicz odległość na planie.
   • Podziel rzeczywistą odległość (w centymetrach) przez drugą liczbę ze skali liczbowej (również w centymetrach).
   • Przykład: 600 cm / 500 = 1,2 cm.
   • Długość pokoju na planie wyniesie 1,2 cm.

Zadanie typ 3: Jak obliczyć skalę mapy, gdy znasz obie odległości?

Ten typ zadania wymaga od nas ustalenia, w jakiej skali została wykonana mapa lub plan.

1. Krok 1: Zapisz obie odległości i przelicz je na tę samą jednostkę.
   • Przykład: Odległość między dwoma punktami na mapie wynosi 4 cm. Rzeczywista odległość to 2 km.
   • Przelicz kilometry na centymetry: 2 km * 100 000 cm/km = 200 000 cm.
2. Krok 2: Ustaw proporcję.
   • Skala to stosunek odległości na mapie do odległości rzeczywistej. Chcemy, aby pierwsza liczba była 1.
   • 4 cm (na mapie) : 200 000 cm (w rzeczywistości)
3. Krok 3: Podziel obie strony proporcji przez odległość na mapie, aby uzyskać 1.
   • 4 cm : 200 000 cm | : 4
   • 1 cm : 50 000 cm
4. Krok 4: Zapisz skalę liczbową.
   • Skala mapy to 1:50 000.

Skale powiększające i pomniejszające: co oznaczają typy 2:1 i 5:1?

Do tej pory omawialiśmy głównie skale pomniejszające, czyli takie, gdzie obiekt w rzeczywistości jest większy niż na rysunku (np. mapa). Istnieją jednak również skale powiększające, które są równie ważne, choć rzadziej spotykane w codziennym życiu.

Kiedy rysunek jest większy od rzeczywistości? Zrozumienie skali powiększającej

Skala powiększająca oznacza, że obiekt na rysunku jest większy niż w rzeczywistości. Zapisujemy ją w formacie, gdzie pierwsza liczba jest większa od drugiej, np. 2:1, 5:1, 10:1. Skala 2:1 oznacza, że 2 cm na rysunku odpowiadają 1 cm w rzeczywistości. Stosuje się ją najczęściej w rysunkach technicznych, aby dokładnie przedstawić bardzo małe elementy, takie jak części zegarków, mikroprocesory czy detale maszyn. Dla uczniów bywa to często mylące, ponieważ intuicyjnie myślimy o skali jako o pomniejszaniu. Warto zapamiętać, że pierwsza liczba zawsze odnosi się do rysunku, a druga do rzeczywistości.

Jak poprawnie stosować skalę powiększającą w zadaniach?

Obliczenia ze skalą powiększającą są analogiczne do tych ze skalą pomniejszającą, ale musimy pamiętać o kierunku. Jeśli skala to 5:1, a rzeczywista długość elementu wynosi 3 mm, to na rysunku będzie on miał 5 razy więcej, czyli 3 mm * 5 = 15 mm (1,5 cm). Jeśli natomiast na rysunku element ma 20 mm, a skala to 4:1, to jego rzeczywista długość to 20 mm / 4 = 5 mm. Zawsze zadaj sobie pytanie: "Czy rysunek ma być większy, czy mniejszy od rzeczywistości?" i odpowiednio mnoż lub dziel.

Najczęstsze pułapki w zadaniach ze skalą: sprawdź, jak ich unikać!

Chciałbym Cię przestrzec przed najczęściej popełnianymi błędami w zadaniach ze skalą. Znając je, będziesz mógł ich świadomie unikać i znacznie poprawisz swoje wyniki.

Błąd nr 1: Chaos w jednostkach jak utrzymać porządek w obliczeniach?

• Problem: Największym i najczęstszym błędem jest mylenie jednostek centymetrów z metrami, metrami z kilometrami. Prowadzi to do całkowicie błędnych wyników.
• Rozwiązanie: Zawsze, ale to zawsze na początku zadania, przeliczaj wszystkie wartości na jedną, wspólną jednostkę. Najczęściej są to centymetry, ponieważ skala liczbowa jest domyślnie w centymetrach (np. 1:100 000 oznacza 1 cm na mapie to 100 000 cm w rzeczywistości). Dopiero po przeliczeniu wszystkich danych na tę samą jednostkę, przystąp do właściwych obliczeń.

Błąd nr 2: Mnożenie zamiast dzielenia (i odwrotnie) prosta metoda na weryfikację wyniku

Często uczniowie mają problem z tym, czy w danym momencie należy pomnożyć, czy podzielić. Jeśli obliczasz rzeczywistą odległość, a masz skalę pomniejszającą (np. 1:100 000), logiczne jest, że rzeczywistość będzie większa niż na mapie, więc musisz pomnożyć. Jeśli obliczasz odległość na mapie, a masz rzeczywistą odległość i skalę pomniejszającą, to na mapie odległość będzie mniejsza, więc musisz podzielić. Zawsze weryfikuj swój wynik: czy ma sens? Czy rzeczywista odległość jest znacznie większa niż ta na mapie (przy skali pomniejszającej)? Jeśli wynik jest mniejszy, a powinien być większy, wiesz, że coś poszło nie tak.

Przeczytaj również: Upraszczanie sum algebraicznych: Krok po kroku do najprostszej postaci

Błąd nr 3: Niezrozumienie zapisu skali jak upewnić się, że dobrze zaczynasz zadanie?

Prawidłowe odczytanie i zrozumienie zapisu skali to podstawa. Skala 1:50 000 nie jest tylko "jedynka do pięćdziesięciu tysięcy". To "jeden centymetr na mapie to pięćdziesiąt tysięcy centymetrów w rzeczywistości". Zawsze staraj się "przetłumaczyć" skalę liczbową na skalę mianowaną (np. 1 cm -> 500 m). To natychmiastowo rozjaśnia sytuację i ułatwia dalsze kroki. Jeśli masz wątpliwości, narysuj sobie malutki odcinek i podpisz, ile to jest w rzeczywistości. To prosta wizualizacja, która bardzo pomaga.