Artykuł to kompleksowy poradnik, który krok po kroku wyjaśnia, jak wyznaczyć równanie prostej w różnych sytuacjach, co jest kluczową umiejętnością na maturze i w zadaniach domowych. Dowiesz się, jak radzić sobie z dwoma punktami, punktem i nachyleniem, oraz prostymi równoległymi i prostopadłymi, by zyskać pewność siebie w rozwiązywaniu zadań.
Opanuj wyznaczanie równania prostej klucz do sukcesu na egzaminie z matematyki
- Równanie prostej występuje w dwóch głównych postaciach: kierunkowej (y = ax + b) i ogólnej (Ax + By + C = 0).
- Współczynnik kierunkowy 'a' określa nachylenie prostej, a wyraz wolny 'b' punkt przecięcia z osią OY.
- Równanie prostej możesz wyznaczyć, mając dwa punkty, lub znając jeden punkt i współczynnik kierunkowy 'a'.
- Dwie proste są równoległe, gdy mają równe współczynniki kierunkowe (a₁ = a₂), a prostopadłe, gdy ich iloczyn wynosi -1 (a₁ * a₂ = -1).
- Umiejętność wyznaczania równania prostej to pewny element zadań maturalnych.
Równanie prostej: co to jest i dlaczego warto je znać?
Równanie prostej to nic innego jak matematyczny opis linii, która rozciąga się w nieskończoność na płaszczyźnie kartezjańskiej. Pozwala ono precyzyjnie określić położenie każdego punktu leżącego na tej prostej. To fundament geometrii analitycznej i jedna z tych umiejętności, które są absolutnie niezbędne w szkole średniej, a szczególnie na egzaminie maturalnym z matematyki.
Z mojego doświadczenia wiem, że opanowanie wyznaczania równania prostej to klucz do sukcesu w wielu zadaniach. Nie tylko tych stricte z geometrii, ale także w kontekście funkcji liniowych czy nawet niektórych zagadnień fizycznych. Dzięki niemu potrafimy nie tylko opisać istniejącą prostą, ale także stworzyć równanie prostej spełniającej określone warunki, co jest często testowane na maturze.
Dwa oblicza tej samej linii: postać kierunkowa kontra ogólna
W matematyce spotkasz się z dwoma głównymi sposobami zapisu równania prostej: postacią kierunkową i ogólną. Chociaż wyglądają inaczej, obie opisują tę samą prostą. To trochę jak mieć dwa różne języki do opisania tego samego obiektu każdy ma swoje zalety i jest użyteczny w innych sytuacjach. Ważne, abyś potrafił swobodnie przechodzić między nimi.
Postać kierunkowa (y = ax + b): co naprawdę mówią Ci litery 'a' i 'b'?
Postać kierunkowa, czyli y = ax + b, jest chyba najbardziej intuicyjna. Litera 'a' to tak zwany współczynnik kierunkowy. Mówi nam on o nachyleniu prostej względem osi OX. Jeśli 'a' jest dodatnie, prosta "idzie w górę", jeśli ujemne "spada". Im większa wartość bezwzględna 'a', tym bardziej stroma jest prosta. Matematycznie rzecz ujmując, 'a' jest równe tangensowi kąta, jaki prosta tworzy z dodatnią półosią OX. Z kolei litera 'b' to wyraz wolny. Oznacza on punkt, w którym prosta przecina oś OY. Jeśli b=0, prosta przechodzi przez początek układu współrzędnych (punkt (0,0)).
Postać ogólna (Ax + By + C = 0): kiedy okazuje się niezastąpiona?
Postać ogólna równania prostej to Ax + By + C = 0, gdzie A, B i C są stałymi, a przynajmniej jedna z nich (A lub B) musi być różna od zera. Ta forma jest szczególnie przydatna, gdy mamy do czynienia z prostymi pionowymi (których nie da się zapisać w postaci kierunkowej, ponieważ współczynnik 'a' byłby nieskończony) lub gdy potrzebujemy obliczyć odległość punktu od prostej. Często też warunki równoległości i prostopadłości łatwiej jest analizować, gdy obie proste są w tej samej postaci ogólnej.
Jak sprawnie żonglować postaciami? Przejście od ogólnej do kierunkowej i z powrotem
Przekształcanie równań między postaciami to podstawowa umiejętność. Aby przejść z postaci ogólnej (Ax + By + C = 0) do kierunkowej (y = ax + b), wystarczy wyznaczyć 'y'. Na przykład, jeśli mamy 2x + 3y - 6 = 0, to przekształcamy: 3y = -2x + 6, a następnie y = (-2/3)x + 2. W ten sposób od razu widzimy, że a = -2/3 i b = 2.
W drugą stronę, z postaci kierunkowej do ogólnej, po prostu przenosimy wszystkie wyrazy na jedną stronę równania, tak aby po drugiej stronie zostało zero. Jeśli mamy y = -2x + 5, to przenosimy wszystko na lewą stronę: 2x + y - 5 = 0. I gotowe! Pamiętaj, że współczynniki A, B, C nie są unikalne można je pomnożyć przez dowolną liczbę różną od zera, a równanie nadal będzie opisywać tę samą prostą (np. 4x + 2y - 10 = 0 to ta sama prosta).
Metoda 1: Wyznaczanie równania prostej z dwóch punktów
Jednym z najczęstszych zadań, z jakim się spotkasz, jest wyznaczenie równania prostej, gdy znasz współrzędne dwóch punktów, przez które ona przechodzi. To klasyka gatunku, która pojawia się w każdym podręczniku i na każdej maturze. Zrozumienie tej metody to podstawa.
Zanim zaczniesz: jak obliczyć współczynnik kierunkowy 'a' ze współrzędnych?
Pierwszym krokiem, niezależnie od tego, którą metodę wybierzesz, jest zazwyczaj obliczenie współczynnika kierunkowego 'a'. Jeśli masz dwa punkty P₁=(x₁, y₁) i P₂=(x₂, y₂), to 'a' obliczysz ze wzoru:
a = (y₂ - y₁) / (x₂ - x₁)
Ten wzór mówi nam, jak bardzo zmienia się 'y' w stosunku do zmiany 'x'. Pamiętaj, że mianownik (x₂ - x₁) nie może być równy zero, bo wtedy mielibyśmy prostą pionową, dla której współczynnik 'a' nie jest zdefiniowany w postaci kierunkowej.
Sposób szybki: gotowy wzór, który oszczędzi Twój czas
Istnieje bezpośredni wzór na równanie prostej przechodzącej przez dwa punkty P₁=(x₁, y₁) i P₂=(x₂, y₂). Ten wzór to:
(y - y₁)(x₂ - x₁) = (y₂ - y₁)(x - x₁)
Jest on niezwykle efektywny, zwłaszcza gdy zależy Ci na czasie na egzaminie. Po prostu podstawiasz współrzędne punktów i przekształcasz do żądanej postaci (najczęściej kierunkowej).
Sposób uniwersalny: jak zbudować i rozwiązać niezawodny układ równań?
Inną, równie skuteczną metodą jest wykorzystanie postaci kierunkowej prostej y = ax + b i zbudowanie układu równań. Jeśli prosta przechodzi przez punkty P₁=(x₁, y₁) i P₂=(x₂, y₂), to współrzędne obu punktów muszą spełniać to równanie. Podstawiasz więc współrzędne każdego punktu do wzoru y = ax + b, otrzymując dwa równania z dwiema niewiadomymi (a i b). Rozwiązanie tego układu równań pozwoli Ci znaleźć wartości 'a' i 'b', a tym samym pełne równanie prostej.
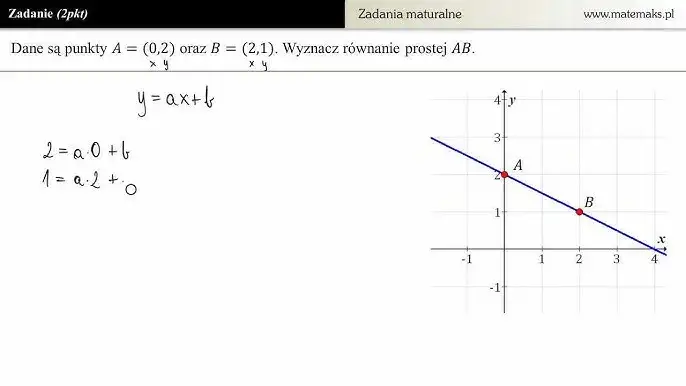
Zobacz to w akcji: rozwiązujemy typowe zadanie maturalne z dwoma punktami
Wyznacz równanie prostej przechodzącej przez punkty A=(1, 2) i B=(3, 8).
Metoda 1: Używając wzoru na współczynnik kierunkowy i podstawienie
-
Oblicz współczynnik kierunkowy 'a':
x₁ = 1, y₁ = 2
x₂ = 3, y₂ = 8
a = (y₂ - y₁) / (x₂ - x₁) = (8 - 2) / (3 - 1) = 6 / 2 = 3 -
Podstaw 'a' i współrzędne jednego punktu do y = ax + b:
Weźmy punkt A=(1, 2) i a = 3:
2 = 3 * 1 + b
2 = 3 + b
b = 2 - 3
b = -1 -
Zapisz równanie prostej:
y = 3x - 1
Metoda 2: Używając układu równań
-
Zbuduj układ równań:
Dla punktu A=(1, 2): 2 = a * 1 + b => a + b = 2
Dla punktu B=(3, 8): 8 = a * 3 + b => 3a + b = 8 -
Rozwiąż układ równań (np. metodą podstawiania lub przeciwnych współczynników):
Z pierwszego równania: b = 2 - a
Podstaw do drugiego: 3a + (2 - a) = 8
2a + 2 = 8
2a = 6
a = 3 -
Oblicz 'b':
b = 2 - a = 2 - 3 = -1 -
Zapisz równanie prostej:
y = 3x - 1
Jak widzisz, obie metody dają ten sam wynik. Wybierz tę, która jest dla Ciebie bardziej zrozumiała i wygodna.
Metoda 2: Jak wyznaczyć równanie prostej, znając punkt i współczynnik kierunkowy?
Innym często spotykanym scenariuszem jest sytuacja, w której znasz jeden punkt, przez który przechodzi prosta, oraz jej współczynnik kierunkowy 'a'. To często bywa łatwiejsze niż praca z dwoma punktami, ponieważ 'a' jest już dane "na tacy".
Kluczowy wzór, który musisz znać: y - y₁ = a(x - x₁)
Do wyznaczenia równania prostej, gdy znasz punkt P₁=(x₁, y₁) i współczynnik kierunkowy 'a', służy wzór:
y - y₁ = a(x - x₁)
Ten wzór jest bardzo intuicyjny. Po prostu podstawiasz do niego znane wartości x₁, y₁ i 'a', a następnie przekształcasz równanie do postaci kierunkowej y = ax + b lub ogólnej, w zależności od wymagań zadania. To naprawdę oszczędza czas!
Od teorii do praktyki: wyznaczamy równanie prostej na konkretnym przykładzie
Wyznacz równanie prostej, która przechodzi przez punkt P=(2, -3) i ma współczynnik kierunkowy a = -2.
-
Podstaw dane do wzoru y - y₁ = a(x - x₁):
x₁ = 2, y₁ = -3, a = -2
y - (-3) = -2(x - 2) -
Uprość i przekształć do postaci kierunkowej:
y + 3 = -2x + 4
y = -2x + 4 - 3
y = -2x + 1
Równanie prostej to y = -2x + 1.
Proste równoległe i prostopadłe: warunki i zastosowanie
Zadania dotyczące prostych równoległych i prostopadłych to niemal pewnik na egzaminach. Wymagają one zrozumienia specyficznych zależności między ich współczynnikami kierunkowymi. Zawsze powtarzam moim uczniom, że to nie jest trudne, wystarczy zapamiętać dwa proste warunki.
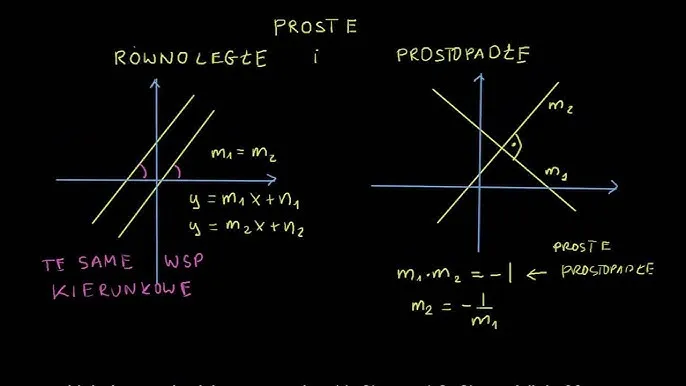
Sekret prostych równoległych: co wspólnego mają ich równania?
Dwie proste są równoległe, jeśli mają to samo nachylenie, czyli ich współczynniki kierunkowe są równe. Jeśli masz dwie proste o równaniach y = a₁x + b₁ i y = a₂x + b₂, to są one równoległe wtedy i tylko wtedy, gdy:
a₁ = a₂
To logiczne skoro mają to samo nachylenie, nigdy się nie przetną (chyba że są tą samą prostą, czyli mają też równe 'b').
Krok po kroku: tworzymy równanie prostej równoległej przechodzącej przez dany punkt
Wyznacz równanie prostej równoległej do prostej y = 3x - 5 i przechodzącej przez punkt P=(1, 4).
-
Odczytaj współczynnik kierunkowy prostej danej:
Dana prosta ma równanie y = 3x - 5, więc jej współczynnik kierunkowy a₁ = 3. -
Wyznacz współczynnik kierunkowy prostej szukanej:
Ponieważ proste mają być równoległe, współczynnik kierunkowy szukanej prostej a₂ musi być równy a₁.
Zatem a₂ = 3. -
Użyj wzoru y - y₁ = a(x - x₁) z punktem P=(1, 4) i a₂ = 3:
y - 4 = 3(x - 1) -
Przekształć do postaci kierunkowej:
y - 4 = 3x - 3
y = 3x - 3 + 4
y = 3x + 1
Równanie szukanej prostej to y = 3x + 1.
Tajemnica kąta prostego: warunek prostopadłości, który musisz zapamiętać
Dwie proste są prostopadłe, jeśli przecinają się pod kątem prostym (90 stopni). Warunek prostopadłości jest nieco bardziej złożony niż równoległości, ale równie łatwy do zapamiętania: iloczyn ich współczynników kierunkowych musi być równy -1. Jeśli masz proste y = a₁x + b₁ i y = a₂x + b₂, to są one prostopadłe, gdy:
a₁ * a₂ = -1
Z tego warunku wynika, że a₂ = -1/a₁. Pamiętaj, że ten warunek nie dotyczy prostych pionowych i poziomych, które są prostopadłe, ale dla których jeden ze współczynników 'a' jest niezdefiniowany, a drugi wynosi 0 (np. x=const i y=const).
Instrukcja krok po kroku: jak znaleźć równanie prostej prostopadłej do innej?
Wyznacz równanie prostej prostopadłej do prostej y = (1/2)x + 3 i przechodzącej przez punkt P=(-2, 5).
-
Odczytaj współczynnik kierunkowy prostej danej:
Dana prosta ma równanie y = (1/2)x + 3, więc jej współczynnik kierunkowy a₁ = 1/2. -
Wyznacz współczynnik kierunkowy prostej szukanej, korzystając z warunku a₁ * a₂ = -1:
(1/2) * a₂ = -1
a₂ = -1 / (1/2)
a₂ = -2 -
Użyj wzoru y - y₁ = a(x - x₁) z punktem P=(-2, 5) i a₂ = -2:
y - 5 = -2(x - (-2))
y - 5 = -2(x + 2) -
Przekształć do postaci kierunkowej:
y - 5 = -2x - 4
y = -2x - 4 + 5
y = -2x + 1
Równanie szukanej prostej to y = -2x + 1.
Unikaj typowych błędów: najczęstsze pułapki przy wyznaczaniu równania prostej
Podczas rozwiązywania zadań z równaniem prostej, łatwo jest wpaść w pewne pułapki. Zwróć uwagę na te najczęstsze, aby ich unikać:
-
Błędy w znakach przy przekształcaniu wzorów
To chyba najczęstszy błąd! Pamiętaj, że przenosząc wyraz na drugą stronę równania, zmieniasz jego znak. Podobnie, bądź bardzo ostrożny przy podstawianiu liczb ujemnych do wzorów, zwłaszcza gdy przed nawiasem jest minus (np. y - (-3) staje się y + 3).
-
Mylenie warunku na równoległość z warunkiem na prostopadłość
Warunki a₁ = a₂ (równoległość) i a₁ * a₂ = -1 (prostopadłość) są do siebie podobne, ale ich skutki są diametralnie różne. Upewnij się, że zawsze stosujesz właściwy warunek do danego problemu.
-
Przeczytaj również: Wzór na obwód trójkąta: Od podstaw do Pitagorasa!
Nieprawidłowe podstawianie współrzędnych (x₁, y₁) do wzoru
Często widzę, jak uczniowie mylą x z y lub podstawiają współrzędne z różnych punktów w niewłaściwe miejsca. Zawsze dokładnie oznaczaj sobie, które współrzędne to x₁, y₁, a które x₂, y₂. Precyzja to podstawa!
Twoja ściągawka: najważniejsze wzory i warunki
Aby ułatwić Ci zapamiętanie kluczowych informacji, przygotowałem małą ściągawkę:
| Nazwa/Opis | Wzór/Warunek |
|---|---|
| Postać kierunkowa prostej | y = ax + b |
| Postać ogólna prostej | Ax + By + C = 0 |
| Współczynnik kierunkowy 'a' (dwa punkty P₁=(x₁, y₁), P₂=(x₂, y₂)) | a = (y₂ - y₁) / (x₂ - x₁) |
| Równanie prostej przez dwa punkty (P₁=(x₁, y₁), P₂=(x₂, y₂)) | (y - y₁)(x₂ - x₁) = (y₂ - y₁)(x - x₁) |
| Równanie prostej przez punkt P₁=(x₁, y₁) i współczynnik 'a' | y - y₁ = a(x - x₁) |
| Warunek równoległości prostych (a₁, a₂ to współczynniki kierunkowe) | a₁ = a₂ |
| Warunek prostopadłości prostych (a₁, a₂ to współczynniki kierunkowe) | a₁ * a₂ = -1 |