Czy rozwiązywanie równań wydaje Ci się skomplikowane? W tym artykule odkryjesz, że matematyka może być prosta i intuicyjna, nawet jeśli dopiero zaczynasz swoją przygodę z równaniami. Pokażemy Ci, jak metoda "zgadywania", czyli prób i błędów, jest potężnym narzędziem, które pomoże Ci zrozumieć podstawy i zbudować pewność siebie w świecie liczb.
Zgadywanie to sprytny start jak metoda prób i błędów pomaga rozwiązywać równania
- Rozwiązywanie równania polega na znalezieniu takiej liczby, która po podstawieniu za niewiadomą (np. x) sprawia, że lewa strona równania jest równa prawej.
- Metoda prób i błędów to intuicyjna strategia, polegająca na podstawianiu kolejnych, logicznie dobranych liczb i sprawdzaniu, czy równanie jest prawdziwe.
- Jest to fundamentalna metoda nauczana w szkole podstawowej, idealna do zrozumienia idei równowagi w równaniach.
- Kluczowym elementem jest także sprawdzenie rozwiązania, aby upewnić się, że znaleziona liczba jest prawidłowa.
- Wizualizacje, takie jak waga szalkowa, znacząco ułatwiają zrozumienie koncepcji równania i znaku równości.
Zgadywanie w matematyce to sprytna metoda na start!
Zgadywanie w matematyce to sprytna metoda na start!
Wielu z nas, słysząc o "zgadywaniu" w kontekście matematyki, może pomyśleć, że to coś niepoważnego, wręcz oszustwo. Nic bardziej mylnego! Jako Alan Szymczak, mogę Cię zapewnić, że metoda prób i błędów, którą potocznie nazywamy zgadywaniem, jest w pełni legalną i niezwykle skuteczną strategią, zwłaszcza dla tych, którzy dopiero stawiają pierwsze kroki w świecie równań. To nie jest unikanie myślenia, lecz świadome i systematyczne poszukiwanie rozwiązania.
W polskim systemie edukacji, szczególnie w szkole podstawowej, metoda ta jest celowo wprowadzana, aby uczniowie mogli w intuicyjny sposób zrozumieć, czym jest równanie i na czym polega jego rozwiązanie. Buduje ona fundamenty pod bardziej zaawansowane techniki, ucząc cierpliwości, logicznego myślenia i weryfikacji. To doskonały sposób, aby oswoić się z abstrakcyjnymi pojęciami i zyskać pewność siebie.
Dlaczego "zgadywanie" jest potężnym narzędziem w rękach początkującego matematyka?
Uważam, że "zgadywanie" jest niczym innym jak matematycznym eksperymentowaniem. Demistyfikuje ono matematykę, sprawiając, że zbiór abstrakcyjnych symboli staje się namacalną zagadką do rozwiązania. Dzięki tej metodzie budujesz intuicję zaczynasz "czuć" liczby i ich relacje. Zamiast mechanicznie stosować wzory, aktywnie myślisz o tym, co dzieje się po obu stronach równania. To naturalny i niezwykle ważny krok, który przygotowuje Cię do zrozumienia bardziej złożonych metod rozwiązywania równań w przyszłości.
Co zyskasz, czytając ten poradnik do końca?
- Zrozumiesz, czym tak naprawdę jest równanie i jak działa jego mechanizm.
- Opanujesz metodę prób i błędów, która pozwoli Ci rozwiązywać proste równania z łatwością.
- Nauczysz się, jak skutecznie sprawdzać swoje rozwiązania, aby mieć pewność co do ich poprawności.
- Zwiększysz swoją pewność siebie w matematyce, postrzegając ją jako logiczną i przyjemną zagadkę, a nie zbiór trudnych do zrozumienia reguł.
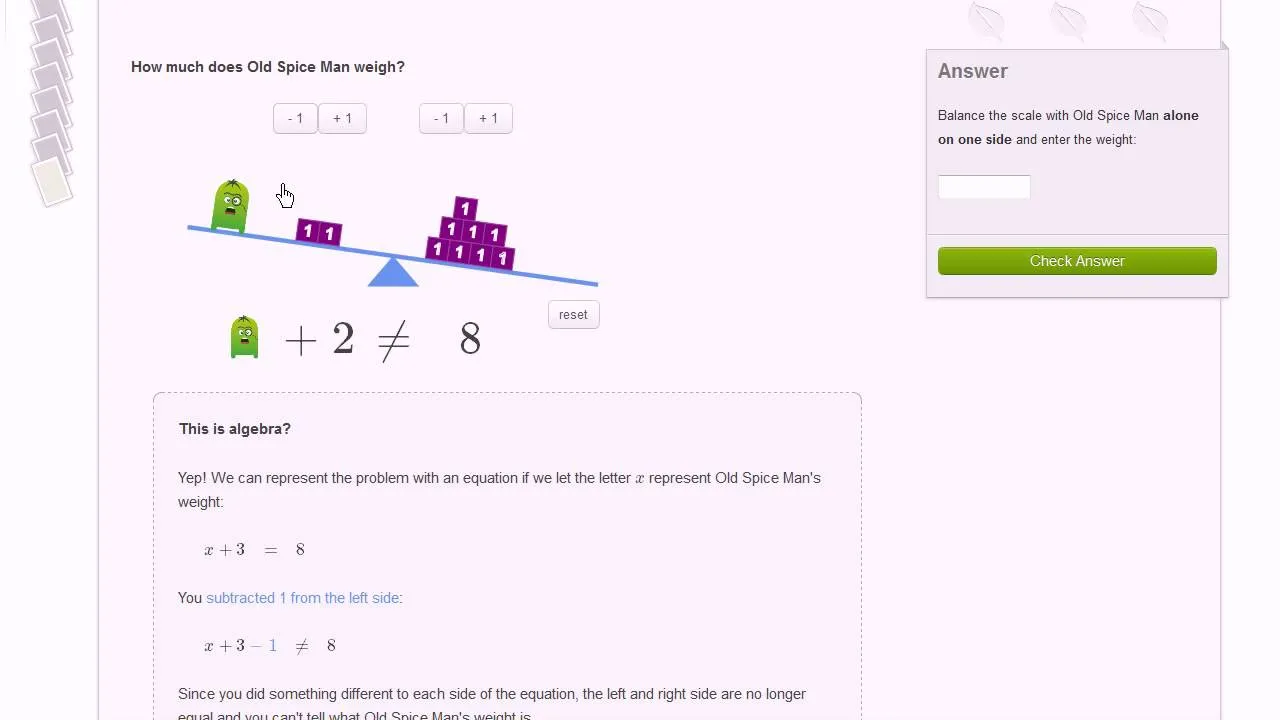
Czym tak naprawdę jest równanie? Wyobraź sobie idealnie wyważoną wagę
Aby zrozumieć równanie, wyobraź sobie starą, klasyczną wagę szalkową. Po jednej stronie kładziesz pewne ciężarki, a po drugiej inne. Aby waga była w równowadze, ciężar po obu stronach musi być identyczny. I dokładnie to samo dzieje się w równaniu! Równanie to nic innego jak matematyczne stwierdzenie, że dwie wartości lub wyrażenia są sobie równe. Naszym zadaniem jest znaleźć to, co sprawi, że ta matematyczna waga będzie idealnie wyważona. To klucz do zrozumienia całej idei.
Tajemnicza niewiadoma czyli kim lub czym jest "x"?
W każdym równaniu pojawia się coś, co nazywamy "niewiadomą". Najczęściej oznaczamy ją literą 'x', ale równie dobrze może to być 'y', 'a' czy jakakolwiek inna litera. Nie ma w niej żadnej tajemnicy! Niewiadoma to po prostu symbol zastępujący konkretną liczbę, której wartości jeszcze nie znamy, ale którą musimy znaleźć. To właśnie ta liczba, po podstawieniu do równania, sprawi, że nasza matematyczna waga będzie w idealnej równowadze. Pomyśl o niej jak o brakującym elemencie układanki.
Znak równości "=" jako serce równania
Znak równości "=" to absolutne serce każdego równania. To on symbolizuje tę idealną równowagę, o której mówiłem. Oznacza, że wartość po lewej stronie tego znaku jest dokładnie taka sama jak wartość po prawej stronie. Jeśli wrócimy do naszej analogii z wagą szalkową, znak równości jest punktem podparcia, który musi pozostać stabilny i prosty, gdy ciężary po obu stronach są identyczne. Bez niego nie byłoby równania, a jedynie wyrażenie matematyczne.
Co to znaczy "rozwiązać równanie" i znaleźć jego pierwiastek?
Kiedy mówimy "rozwiązać równanie", mamy na myśli nic innego, jak znalezienie tej konkretnej liczby (lub liczb), która po podstawieniu w miejsce niewiadomej sprawi, że równanie stanie się prawdziwe czyli lewa strona będzie równa prawej. Tę znalezioną liczbę nazywamy "rozwiązaniem równania" lub "pierwiastkiem równania". To właśnie ten pierwiastek jest kluczem, który otwiera drzwi do równowagi w naszym matematycznym świecie.Metoda prób i błędów jak zostać matematycznym detektywem
Teraz, gdy już wiesz, czym jest równanie i jego elementy, czas na naszą detektywistyczną przygodę! Metoda prób i błędów to nic innego jak systematyczna gra w "ciepło-zimno", w której naszym celem jest odnalezienie tej jednej, jedynej liczby, która pasuje do równania. Przygotuj się na bycie matematycznym detektywem!
Krok 1: Twoje pierwsze podejrzenie jak mądrze wybrać pierwszą liczbę do sprawdzenia?
Zaczynamy od wyboru "podejrzanego" czyli pierwszej liczby, którą podstawimy za niewiadomą. Nie rzucajmy się od razu na losowe, duże liczby. Moja rada? Zacznij od małych, całkowitych liczb, takich jak 0, 1, 2, 3, -1, -2. Często w prostych równaniach rozwiązanie kryje się właśnie wśród nich. Możesz też spróbować oszacować: jeśli masz równanie `x + 5 = 10`, to wiesz, że 'x' musi być mniejsze od 10. Spróbuj więc liczb, które wydają się "bliskie" oczekiwanemu wynikowi. To nie jest strzelanie w ciemno, to przemyślany pierwszy ruch.
Krok 2: Sprawdzenie alibi czyli podstawienie liczby i weryfikacja równości
Kiedy już wybierzesz swoją pierwszą liczbę, czas na "sprawdzenie alibi". Podstaw tę liczbę w miejsce niewiadomej w równaniu i wykonaj wszystkie obliczenia po obu stronach znaku równości. Na przykład, jeśli masz `x + 7 = 15` i wybrałeś `x = 5`, podstawiasz: `5 + 7 = 12`. Następnie porównujesz wynik (12) z liczbą po prawej stronie równania (15). Czy są równe? Jeśli nie, to znaczy, że nasza liczba nie jest rozwiązaniem.
Krok 3: Za ciepło, za zimno jak korygować kolejne próby, by trafić w dziesiątkę?
Teraz wkracza gra w "za ciepło, za zimno". Jeśli w poprzednim kroku lewa strona równania okazała się za mała (np. 12 zamiast 15), to znaczy, że potrzebujemy większej liczby dla 'x'. Spróbuj więc kolejnej, większej liczby. Jeśli natomiast lewa strona była za duża, spróbuj mniejszej liczby. Analizuj wyniki każdej próby. To nie jest bezmyślne zgadywanie, lecz logiczne zawężanie pola poszukiwań. Każda nieudana próba dostarcza cennych informacji, które przybliżają Cię do rozwiązania.
Praktyczny przykład: Rozwiążmy razem równanie `x + 7 = 15`
Rozwiążmy to równanie krok po kroku, stosując metodę prób i błędów:
- Wybierz pierwszą liczbę: Spróbujmy `x = 5`.
- Podstaw i oblicz: `5 + 7 = 12`.
- Porównaj: `12 ≠ 15`. Lewa strona jest za mała. Potrzebujemy większej liczby.
- Skoryguj próbę: Spróbujmy `x = 8`.
- Podstaw i oblicz: `8 + 7 = 15`.
- Porównaj: `15 = 15`. Rozwiązanie znalezione! Liczba 8 jest pierwiastkiem tego równania.
Jak sprawdzić, czy Twoja "zgadnięta" liczba jest poprawna?
Znalezienie rozwiązania metodą prób i błędów to świetny początek, ale prawdziwy matematyczny detektyw zawsze weryfikuje swoje odkrycia. Sprawdzenie rozwiązania to ostatni, ale niezwykle ważny krok, który daje Ci 100% pewności, że Twoja "zgadnięta" liczba jest tą właściwą.
Na czym polega sprawdzanie rozwiązania i dlaczego jest tak ważne?
Sprawdzanie rozwiązania polega na podstawieniu znalezionej wartości niewiadomej z powrotem do oryginalnego równania i wykonaniu wszystkich obliczeń. Jeśli po podstawieniu i obliczeniach lewa strona równania jest równa prawej, to masz pewność, że Twoje rozwiązanie jest poprawne. Dlaczego to takie ważne? Po pierwsze, buduje Twoją pewność siebie wiesz, że nie tylko znalazłeś liczbę, ale i udowodniłeś jej poprawność. Po drugie, pozwala wyłapać ewentualne błędy, które mogły pojawić się podczas "zgadywania". Po trzecie, wzmacnia Twoje zrozumienie idei równowagi w równaniu, utrwalając kluczową koncepcję.
Przykład krok po kroku: Weryfikacja wyniku w równaniu `3 * y = 21`
Załóżmy, że metodą prób i błędów znaleźliśmy rozwiązanie `y = 7`. Sprawdźmy, czy jest ono poprawne:
- Oryginalne równanie: `3 * y = 21`
- Podstawienie znalezionego rozwiązania: W miejsce 'y' wstawiamy 7. Otrzymujemy: `3 * 7 = 21`
- Obliczenia: Wykonujemy mnożenie po lewej stronie: `21 = 21`
- Wniosek: Obie strony równania są sobie równe. Rozwiązanie `y = 7` jest poprawne!
Kiedy zgadywanie to za mało? Pułapki metody prób i błędów
Metoda prób i błędów jest fantastyczna do nauki podstaw i rozwiązywania prostych równań. Jednak, jak każde narzędzie, ma swoje ograniczenia. Ważne jest, abyś wiedział, kiedy "zgadywanie" może okazać się niewystarczające, abyś mógł płynnie przejść do bardziej zaawansowanych technik.
Dlaczego przy większych liczbach lub ułamkach ta metoda staje się niepraktyczna?
Wyobraź sobie, że musisz rozwiązać równanie, w którym wynik to bardzo duża liczba, np. `x + 1234 = 5678`, albo co gorsza, ułamek lub liczba dziesiętna, np. `2 * x = 7.5`. "Zgadywanie" w takich przypadkach staje się nieefektywne i czasochłonne, a czasem wręcz niemożliwe do wykonania w rozsądnym czasie. Szukanie igły w stogu siana to jedno, ale szukanie konkretnego ziarenka piasku na plaży to już zupełnie inna bajka. Dlatego, choć start z tą metodą jest świetny, musimy być świadomi jej ograniczeń.
Co zrobić, gdy rozwiązań jest więcej niż jedno (lub nie ma go wcale)?
Warto również wiedzieć, że nie wszystkie równania mają jedno, unikalne rozwiązanie, które łatwo "zgadnąć". Niektóre, bardziej złożone równania (np. równania kwadratowe) mogą mieć dwa rozwiązania, a nawet więcej! Co więcej, istnieją równania, które nie mają żadnego rozwiązania w zbiorze liczb rzeczywistych. Metoda prób i błędów najlepiej sprawdza się w przypadku prostych równań liniowych z jedną niewiadomą, które mają jedno, konkretne rozwiązanie. W innych przypadkach potrzebne są bardziej zaawansowane metody.
Od zgadywania do pewności co dalej po opanowaniu podstaw?
Gratulacje! Opanowałeś podstawy rozwiązywania równań metodą prób i błędów. To solidny fundament. Teraz czas spojrzeć w przyszłość i zobaczyć, jak możesz rozwijać swoje umiejętności, aby radzić sobie z coraz trudniejszymi wyzwaniami matematycznymi.
Krótkie wprowadzenie do przekształcania równań (idea przenoszenia na drugą stronę)
Gdy już dobrze rozumiesz ideę równowagi w równaniu, kolejnym krokiem jest nauka przekształceń algebraicznych. To bardziej systematyczny sposób rozwiązywania, który polega na wykonywaniu tych samych operacji (dodawanie, odejmowanie, mnożenie, dzielenie) po obu stronach równania, aby zachować równowagę i "wyizolować" niewiadomą. Często mówi się o "przenoszeniu" wyrazów na drugą stronę ze zmianą znaku to nic innego jak skrót myślowy dla tych operacji. Ta metoda jest szybsza i skuteczniejsza, zwłaszcza przy bardziej skomplikowanych równaniach.
Jak narzędzia online i aplikacje mogą pomóc Ci w ćwiczeniach?
W dzisiejszych czasach masz dostęp do mnóstwa fantastycznych narzędzi, które pomogą Ci w dalszej nauce. Platformy takie jak Matlandia, Khan Academy czy różne aplikacje edukacyjne oferują interaktywne ćwiczenia, wizualizacje i gry, które sprawiają, że nauka staje się jeszcze przyjemniejsza. Możesz tam ćwiczyć rozwiązywanie równań, sprawdzać swoje wyniki i uczyć się nowych metod w angażujący sposób. Wykorzystaj je, aby wzmocnić swoje umiejętności!
Twoja nowa supermoc w matematyce podsumowanie i zachęta
Pamiętaj, "zgadywanie" to nie jest słabość, lecz strategia. To Twoja pierwsza supermoc w świecie równań, która pozwoliła Ci zrozumieć ich istotę i zbudować solidne podstawy. Jesteś na dobrej drodze do zostania mistrzem matematyki!
Kluczowe wnioski: Dlaczego warto zacząć od "zgadywania"?
- Buduje intuicję: Pomaga "poczuć" liczby i zrozumieć, jak działają równania, zanim przejdziesz do abstrakcyjnych reguł.
- Demistyfikuje równania: Sprawia, że matematyka staje się bardziej przystępna i mniej przerażająca.
- Stanowi solidną podstawę: Zrozumienie równowagi i celu rozwiązywania równań jest kluczowe dla dalszej nauki.
- Sprawia, że matematyka staje się przyjemna: Proces poszukiwania rozwiązania może być traktowany jak ekscytująca zagadka.
Przeczytaj również: Kwadrat magiczny: Odkryj sekrety i zbuduj swój 3x3!
Jak regularne ćwiczenia zamienią Cię w mistrza równań?
Jak w każdej dziedzinie, kluczem do sukcesu jest regularna praktyka. Nie bój się eksperymentować z liczbami, popełniać błędów i uczyć się na nich. Im więcej równań rozwiążesz, tym szybciej i pewniej będziesz działać. Każde rozwiązane równanie to małe zwycięstwo, które buduje Twoją pewność siebie i biegłość. Wkrótce zobaczysz, że rozwiązywanie równań stanie się dla Ciebie drugą naturą, a matematyka fascynującą przygodą!