Jak obliczać układy równań? Zrozum metody i unikaj pułapek.

Układy równań to fundament matematyki, który pozwala nam rozwiązywać problemy z wieloma niewiadomymi jednocześnie. Zrozumienie ich działania jest kluczowe nie tylko w szkole, ale i w wielu praktycznych zastosowaniach. W tym artykule pokażę Ci krok po kroku, jak opanować najważniejsze metody rozwiązywania układów równań, dzięki czemu zyskasz pewność siebie w obliczeniach.

Czym tak naprawdę jest układ równań i gdzie go spotkasz?

Układ równań to po prostu zbiór dwóch lub więcej równań, które zawierają dwie lub więcej niewiadomych, a my szukamy wartości tych niewiadomych, które spełniają wszystkie równania jednocześnie. To trochę jak detektywistyczna zagadka, gdzie każda wskazówka (równanie) prowadzi nas do rozwiązania. Spotkasz je wszędzie od zadań z matematyki, gdzie obliczasz wiek osób czy wymiary figur geometrycznych, przez fizykę (np. ruch ciał), po ekonomię (np. optymalizacja kosztów) czy nawet codzienne życie, gdy próbujesz ustalić cenę dwóch różnych produktów, znając ich łączny koszt i pewne zależności między nimi. Na przykład, jeśli wiesz, że kupiłeś łącznie 5 jabłek i bananów za 10 zł, a banan jest dwa razy droższy od jabłka, to właśnie masz układ równań do rozwiązania!

Trzy możliwe wyniki, czyli co może wyjść z obliczeń?

Kiedy rozwiązujesz układ równań, możesz otrzymać jeden z trzech typów wyników. To bardzo ważne, aby je rozróżniać:

• Układ oznaczony: Otrzymujesz dokładnie jedno, konkretne rozwiązanie, czyli jedną parę liczb (x, y), która spełnia oba równania. Graficznie oznacza to, że dwie proste, które są interpretacją Twoich równań, przecinają się w jednym punkcie.
• Układ nieoznaczony: W tym przypadku istnieje nieskończenie wiele rozwiązań. Dzieje się tak, gdy jedno równanie jest tak naprawdę przekształceniem drugiego, co oznacza, że masz do czynienia z dwoma identycznymi równaniami. Graficznie proste pokrywają się, mając nieskończenie wiele punktów wspólnych.
• Układ sprzeczny: To sytuacja, w której nie ma żadnego rozwiązania. Oznacza to, że nie istnieje żadna para liczb (x, y), która spełniałaby oba równania jednocześnie. Graficznie proste są równoległe i nigdy się nie przetną.

Metoda podstawiania Twój pierwszy krok do rozwiązania układu

Metoda podstawiania to jedna z najbardziej intuicyjnych technik rozwiązywania układów równań. Polega ona na wyznaczeniu jednej niewiadomej z jednego równania i wstawieniu jej do drugiego. To jak układanie puzzli najpierw identyfikujesz jeden element, a potem dopasowujesz go do reszty.

Instrukcja krok po kroku: jak wyznaczyć i podstawić niewiadomą?

1. Wybierz równanie i wyznacz niewiadomą: Zdecyduj, z którego równania będzie Ci najłatwiej wyznaczyć jedną z niewiadomych (x lub y). Szukaj równania, w którym niewiadoma ma współczynnik 1 lub -1, aby uniknąć ułamków. Przykładowo, jeśli masz równanie x + 2y = 5, łatwo wyznaczysz x = 5 - 2y.
2. Podstaw wyznaczoną niewiadomą do drugiego równania: Teraz, gdy masz wyrażenie na jedną niewiadomą (np. x = 5 - 2y), wstaw je w miejsce tej niewiadomej do drugiego równania układu. Pamiętaj, aby podstawić wyrażenie za każdym razem, gdy ta niewiadoma występuje.
3. Rozwiąż równanie z jedną niewiadomą: Po podstawieniu otrzymasz jedno równanie z tylko jedną niewiadomą. Rozwiąż je, aby znaleźć jej wartość. To jest ten moment, kiedy Twoje równanie upraszcza się do czegoś, co już dobrze znasz.
4. Oblicz wartość drugiej niewiadomej: Gdy masz już wartość jednej niewiadomej (np. y), wróć do wyrażenia, które wyznaczyłeś w kroku pierwszym (np. x = 5 - 2y) i podstaw do niego obliczoną wartość. W ten sposób znajdziesz wartość drugiej niewiadomej (x).

Praktyczny przykład: rozwiązujemy wspólnie pierwszy układ równań

Przyjrzyjmy się temu na konkretnym przykładzie. Rozwiążmy układ:

1. x + 2y = 7

2. 3x - y = 0

Krok 1: Wyznaczam x z pierwszego równania.

x = 7 - 2y

Krok 2: Podstawiam to wyrażenie do drugiego równania.

3 * (7 - 2y) - y = 0

Krok 3: Rozwiązuję równanie z jedną niewiadomą (y).

21 - 6y - y = 0

21 - 7y = 0

-7y = -21

y = 3

Krok 4: Obliczam drugą niewiadomą (x).

x = 7 - 2 * 3

x = 7 - 6

x = 1

Rozwiązaniem układu jest para liczb (1, 3).

Na co uważać? Potencjalne pułapki w tej metodzie

Mimo prostoty, metoda podstawiania ma swoje pułapki, na które warto zwrócić uwagę:

• Błędne wyznaczenie niewiadomej: Upewnij się, że poprawnie przenosisz wyrazy na drugą stronę równania i zmieniasz ich znaki. To najczęstszy błąd na start.
• Pomyłki w znakach podczas podstawiania: Kiedy podstawiasz całe wyrażenie, zwłaszcza gdy przed nim stoi minus lub liczba, użyj nawiasów. Na przykład, jeśli masz - (2y + 1), to po opuszczeniu nawiasu otrzymasz -2y - 1.
• Zapominanie o obliczeniu drugiej niewiadomej: Często zdarza się, że po znalezieniu jednej wartości (np. y) zapominamy wrócić i obliczyć drugą (x). Pamiętaj, że rozwiązaniem układu jest zawsze para liczb!

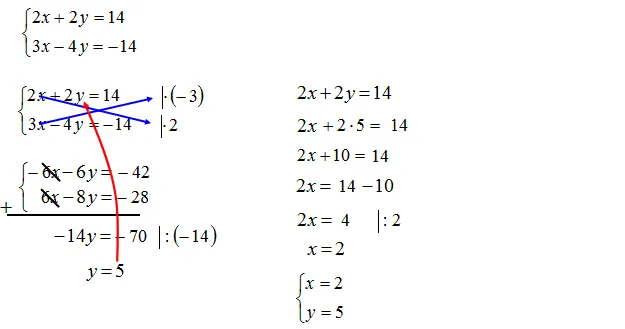
Metoda przeciwnych współczynników sprytny sposób na redukcję

Metoda przeciwnych współczynników, zwana również metodą dodawania stronami, to elegancki sposób na szybkie pozbycie się jednej z niewiadomych. Jej idea polega na takim przekształceniu równań, aby po ich dodaniu stronami jedna z niewiadomych po prostu zniknęła.

Jak stworzyć przeciwne współczynniki? Prosta recepta

Aby zastosować tę metodę, musisz doprowadzić do sytuacji, w której współczynniki przy tej samej niewiadomej w obu równaniach są liczbami przeciwnymi (np. 2x i -2x, 5y i -5y). Często wymaga to pomnożenia jednego lub obu równań przez odpowiednią liczbę. Pamiętaj, że mnożąc równanie, musisz pomnożyć każdy wyraz zarówno po lewej, jak i po prawej stronie znaku równości. To klucz do zachowania równowagi równania. Kiedy już masz przeciwne współczynniki, dodajesz równania stronami: lewą stronę do lewej, prawą do prawej. Jedna niewiadoma się zredukuje, a Ty otrzymasz proste równanie z jedną niewiadomą.

Od mnożenia do rozwiązania: przechodzimy przez cały proces na przykładzie

Rozwiążmy ten sam układ, co poprzednio, ale tym razem metodą przeciwnych współczynników:

1. x + 2y = 7

2. 3x - y = 0

Widzę, że w pierwszym równaniu mam +2y, a w drugim -y. Aby współczynniki przy 'y' były przeciwne, wystarczy pomnożyć drugie równanie przez 2.

Krok 1: Mnożę drugie równanie przez 2.

1. x + 2y = 7

2. 2 * (3x - y) = 2 * 0 => 6x - 2y = 0

Krok 2: Dodaję równania stronami.

(x + 2y) + (6x - 2y) = 7 + 0

x + 6x + 2y - 2y = 7

7x = 7

Krok 3: Rozwiązuję równanie z jedną niewiadomą (x).

x = 1

Krok 4: Podstawiam obliczoną wartość x do jednego z początkowych równań (np. do drugiego, bo jest prostsze).

3 * 1 - y = 0

3 - y = 0

-y = -3

y = 3

Ponownie otrzymaliśmy rozwiązanie (1, 3). Widzisz, że wynik jest ten sam, ale droga do niego nieco inna.

Kiedy ta metoda sprawdza się lepiej niż podstawianie?

Metoda przeciwnych współczynników często okazuje się bardziej efektywna, gdy:

• Współczynniki są już proste lub łatwo je doprowadzić do postaci przeciwnej: Jeśli wystarczy pomnożyć tylko jedno równanie przez małą liczbę, aby uzyskać przeciwne współczynniki, ta metoda będzie szybsza.
• Chcemy uniknąć ułamków: Czasami wyznaczenie niewiadomej w metodzie podstawiania prowadzi do ułamków, co może skomplikować dalsze obliczenia. Metoda przeciwnych współczynników często pozwala ich uniknąć.
• Współczynniki są duże: Jeśli współczynniki są duże, ale łatwo znaleźć ich wspólną wielokrotność, metoda przeciwnych współczynników może uprościć obliczenia.

Metoda graficzna zobacz rozwiązanie na własne oczy

Metoda graficzna to świetny sposób na wizualizację układu równań i zrozumienie, co tak naprawdę oznacza jego rozwiązanie. Polega ona na narysowaniu prostych odpowiadających każdemu równaniu i znalezieniu ich punktu przecięcia.

Jak przekształcić równanie, by narysować prostą?

Aby narysować prostą, musisz przekształcić każde równanie układu do postaci kierunkowej, czyli y = ax + b. W tej postaci 'a' to współczynnik kierunkowy (mówi o nachyleniu prostej), a 'b' to wyraz wolny (punkt przecięcia z osią y). Oto jak to zrobić:

1. Przenieś wszystkie wyrazy z 'x' i stałe na prawą stronę: Pozostaw 'y' (lub wyraz z 'y') po lewej stronie równania.
2. Podziel przez współczynnik przy 'y': Jeśli 'y' ma współczynnik inny niż 1, podziel całe równanie przez ten współczynnik.
3. Znajdź dwa punkty: Aby narysować prostą, wystarczą dwa punkty. Najłatwiej jest podstawić za x=0 (wtedy y=b) i za y=0 (wtedy x=-b/a) lub wybrać inne dwie wygodne wartości x.

Rysujemy i odczytujemy: interpretacja punktu przecięcia

Kiedy już masz przekształcone równania i wyznaczone punkty, narysuj układ współrzędnych i zaznacz te punkty, a następnie poprowadź przez nie proste. Punkt, w którym te dwie proste się przetną, jest rozwiązaniem Twojego układu równań. Współrzędne tego punktu (x, y) to szukane wartości! Pamiętaj, że dokładność rysowania jest tutaj kluczowa im precyzyjniej narysujesz proste, tym dokładniej odczytasz rozwiązanie. Warto używać linijki i papieru w kratkę.

Co oznaczają proste równoległe i pokrywające się?

Interpretacja graficzna pozwala nam również łatwo rozpoznać typ układu:

• Proste równoległe: Jeśli narysujesz dwie proste, które są równoległe i nigdy się nie przecinają, oznacza to, że układ jest sprzeczny i nie ma rozwiązania. Dzieje się tak, gdy współczynniki kierunkowe 'a' obu prostych są takie same, ale wyraz wolny 'b' jest różny.
• Proste pokrywające się: Jeśli obie proste leżą dokładnie na sobie, oznacza to, że układ jest nieoznaczony i ma nieskończenie wiele rozwiązań. Dzieje się tak, gdy oba równania są w rzeczywistości tym samym równaniem, a co za tym idzie, mają identyczne współczynniki 'a' i 'b'.

Jak rozpoznać, z jakim typem układu masz do czynienia?

Rozpoznanie typu układu równań jest kluczowe, bo pozwala przewidzieć, ile rozwiązań powinieneś oczekiwać. Możesz to zrobić zarówno algebraicznie, jak i graficznie, choć w praktyce częściej polegamy na obliczeniach.

Układ oznaczony: jedno konkretne rozwiązanie

Kiedy rozwiązujesz układ równań metodą podstawiania lub przeciwnych współczynników i w końcu otrzymujesz konkretne wartości dla x i y (np. x=2, y=3), to znak, że masz do czynienia z układem oznaczonym. To jest najbardziej typowy i pożądany wynik. Graficznie, jak już wspominałem, oznacza to, że proste reprezentujące Twoje równania przecinają się w jednym, konkretnym punkcie.

Układ nieoznaczony: nieskończenie wiele możliwości

Jeśli podczas rozwiązywania układu równań (metodą algebraiczną) w pewnym momencie wszystkie niewiadome znikają, a Ty otrzymujesz tożsamość, czyli prawdziwe stwierdzenie (np. 0 = 0, 5 = 5, 2x = 2x), to oznacza, że układ jest nieoznaczony. Taki układ ma nieskończenie wiele rozwiązań, ponieważ jedno równanie jest zależne od drugiego są one równoważne. Graficznie proste reprezentujące te równania pokrywają się, tworząc jedną linię.

Układ sprzeczny: czyli sytuacja bez wyjścia

Sytuacja, w której podczas rozwiązywania algebraicznego wszystkie niewiadome znikają, ale otrzymujesz sprzeczność, czyli fałszywe stwierdzenie (np. 0 = 5, 1 = -3), wskazuje na układ sprzeczny. Oznacza to, że nie ma żadnego rozwiązania, które spełniałoby oba równania jednocześnie. Graficznie proste reprezentujące te równania są równoległe i nigdy się nie przetną.

Najczęstsze błędy i jak ich unikać

Nawet doświadczonym matematykom zdarzają się błędy, szczególnie przy długich obliczeniach. W układach równań pewne pułapki pojawiają się nagminnie. Jako Alan Szymczak, widziałem je setki razy i wiem, jak ich unikać.

Uwaga na znaki: pułapka liczb ujemnych

Liczby ujemne to prawdziwy "zabójca" poprawnych wyników. Najczęstsze błędy to:

• Mnożenie przez liczbę ujemną: Zapominamy zmienić znaki wszystkich wyrazów w nawiasie lub w równaniu. Pamiętaj, że minus razy minus daje plus!
• Odejmowanie wyrażeń: Jeśli odejmujesz całe wyrażenie, a przed nim stoi minus, musisz zmienić znaki wszystkich wyrazów w odejmowanym wyrażeniu. Np. -(x - y) to -x + y.
• Przenoszenie wyrazów na drugą stronę: Zawsze, gdy przenosisz wyraz na drugą stronę znaku równości, musisz zmienić jego znak na przeciwny.

Moja rada: zawsze dokładnie sprawdzaj znaki, szczególnie po każdym kroku, w którym występują liczby ujemne.

Błędy przy mnożeniu i przenoszeniu jak zachować porządek w obliczeniach?

• Mnożenie wszystkich wyrazów: Gdy mnożysz równanie przez jakąś liczbę (np. w metodzie przeciwnych współczynników), musisz pomnożyć każdy wyraz w tym równaniu, zarówno po lewej, jak i po prawej stronie znaku równości. Często zapomina się o pomnożeniu wyrazu wolnego.
• Prawidłowe przenoszenie: Zawsze pamiętaj o zmianie znaku przenoszonego wyrazu. Jeśli przenosisz +2x, po drugiej stronie będzie -2x.
• Utrzymywanie porządku: Pisz czytelnie, krok po kroku. Nie próbuj robić zbyt wielu operacji w jednej linii. Im bardziej uporządkowane są Twoje obliczenia, tym łatwiej będzie Ci znaleźć ewentualny błąd. Używaj oddzielnych linii dla każdego kroku.

Sprawdzanie wyniku: Twoja siatka bezpieczeństwa

To jest absolutnie kluczowa wskazówka, którą zawsze daję moim uczniom: zawsze sprawdzaj swoje rozwiązanie! Po znalezieniu pary liczb (x, y), podstaw je do obu początkowych równań układu. Jeśli obie strony każdego równania będą sobie równe, to masz pewność, że Twoje rozwiązanie jest poprawne. Jeśli nie, wiesz, że gdzieś popełniłeś błąd i musisz go znaleźć. To prosta, ale niezwykle skuteczna metoda weryfikacji, która oszczędzi Ci wiele frustracji.

Od teorii do praktyki: rozwiązywanie zadań tekstowych

Układy równań to potężne narzędzie do rozwiązywania zadań tekstowych. Największym wyzwaniem jest często nie samo rozwiązanie układu, ale jego poprawne ułożenie na podstawie treści zadania. Pokażę Ci, jak to zrobić.

Analiza treści: jak "wyciągnąć" równania z zadania?

1. Przeczytaj zadanie ze zrozumieniem: Najpierw dokładnie przeczytaj zadanie, aby zrozumieć, o co w nim chodzi i co masz obliczyć.
2. Zidentyfikuj niewiadome: Zastanów się, jakie wielkości są nieznane i przypisz im zmienne, np. x i y. Zapisz, co oznacza każda zmienna (np. "x - wiek Anny", "y - wiek Piotra").
3. Przetłumacz informacje na równania: Każde zdanie lub fragment tekstu, który zawiera informację o zależnościach między niewiadomymi, spróbuj przetłumaczyć na równanie. Szukaj słów kluczowych, takich jak "suma", "różnica", "iloczyn", "o ile więcej/mniej", "razy więcej/mniej". Pamiętaj, że do ułożenia układu z dwiema niewiadomymi potrzebujesz zazwyczaj dwóch niezależnych informacji, czyli dwóch równań.
4. Typowe zadania tekstowe:
   • Zadania "z wiekiem": "Ania jest o 5 lat starsza od Tomka", "za 3 lata ich wiek będzie sumował się do...".
   • Zadania geometryczne: "Obwód prostokąta wynosi 20 cm, a jeden bok jest o 2 cm dłuższy od drugiego".
   • Zadania o mieszaninach/roztworach: "Mamy dwa roztwory o różnym stężeniu, chcemy uzyskać roztwór o nowym stężeniu".
   • Zadania o prędkości, drodze, czasie: "Samochód jechał z różnymi prędkościami na dwóch odcinkach trasy".

Przeczytaj również: Jak rozwiązać równanie? Spróbuj zgadnąć! Proste metody

Przykład z życia wzięty: rozwiązujemy zadanie tekstowe od A do Z

Wyobraź sobie takie zadanie:

W sklepie zoologicznym są psy i papugi. Wszystkie zwierzęta mają łącznie 10 głów i 28 nóg. Ile jest psów, a ile papug?

Krok 1: Analiza i przypisanie niewiadomych.

Mamy dwa rodzaje zwierząt: psy i papugi. Szukamy ich liczby.

• Niech x oznacza liczbę psów.
• Niech y oznacza liczbę papug.

Krok 2: Ułożenie równań.

1. "Wszystkie zwierzęta mają łącznie 10 głów." Każde zwierzę ma jedną głowę, więc:

x + y = 10

2. "Wszystkie zwierzęta mają łącznie 28 nóg." Pies ma 4 nogi, papuga ma 2 nogi, więc:

4x + 2y = 28

Mamy układ równań:

1. x + y = 10

2. 4x + 2y = 28

Krok 3: Rozwiązanie układu (wybiorę metodę podstawiania).

Z pierwszego równania wyznaczam x: x = 10 - y

Podstawiam do drugiego równania:

4 * (10 - y) + 2y = 28

40 - 4y + 2y = 28

40 - 2y = 28

-2y = 28 - 40

-2y = -12

y = 6

Teraz obliczam x:

x = 10 - 6

x = 4

Krok 4: Sformułowanie odpowiedzi.

W sklepie zoologicznym są 4 psy i 6 papug.