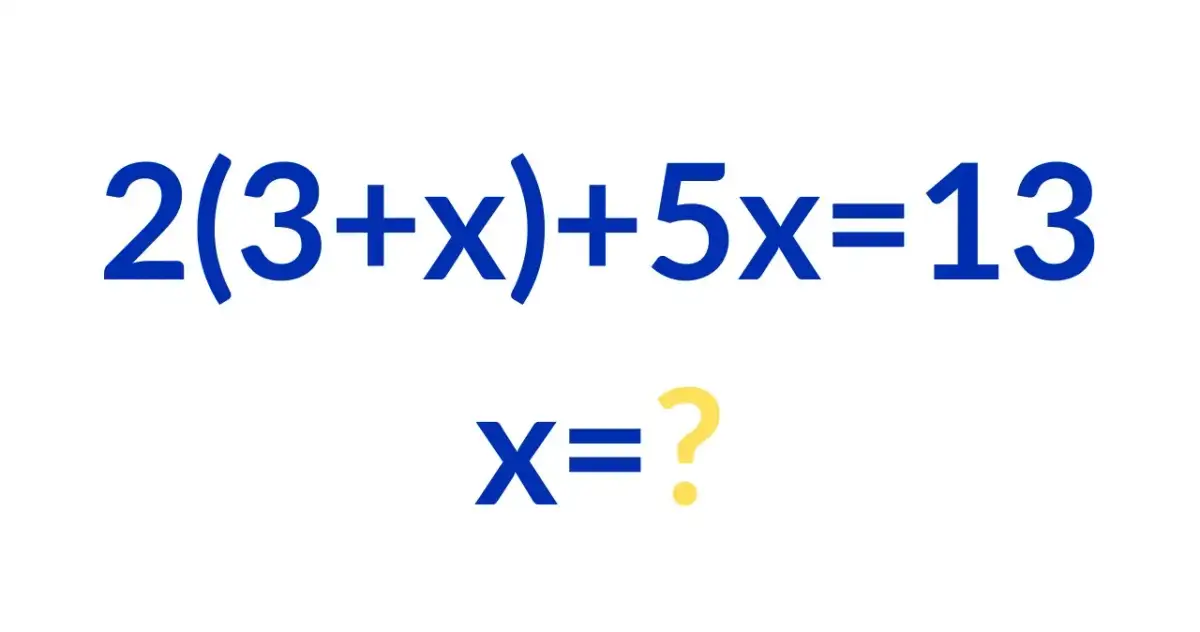Sprawdzenie równania to nic innego jak weryfikacja, czy znalezione przez nas rozwiązanie jest faktycznie poprawne. To kluczowa umiejętność dla każdego ucznia, która nie tylko pomaga uniknąć błędów, ale także buduje pewność siebie w matematyce i pogłębia zrozumienie algebry. Z mojego doświadczenia wiem, że regularne sprawdzanie wyników to najlepsza droga do mistrzostwa.
Sprawdzanie równania klucz do pewności, że Twój wynik jest poprawny
- Na czym polega sprawdzenie? Polega na podstawieniu obliczonej wartości niewiadomej (np. 'x') z powrotem do pierwotnego równania.
- Jaki jest cel sprawdzania? Głównym celem jest weryfikacja poprawności rozwiązania, co pozwala na samodzielne wyłapywanie i korygowanie błędów.
- Kluczowy warunek poprawności: Rozwiązanie jest poprawne, jeśli po podstawieniu i obliczeniach lewa strona równania (L) równa się prawej stronie (P).
- Uniwersalność metody: Metoda sprawdzania jest skuteczna i stosowalna dla różnego rodzaju równań od prostych liniowych, przez te z ułamkami, po równania z nawiasami.
- Korzyści: Regularne sprawdzanie buduje pewność siebie, rozwija logiczne myślenie i pogłębia zrozumienie zasad rządzących algebrą.
Zastanawiasz się, po co w ogóle zawracać sobie głowę sprawdzaniem równania, skoro już je rozwiązałeś? Odpowiedź jest prosta: weryfikacja wyniku jest absolutnie kluczowym elementem procesu rozwiązywania zadań. Pozwala ona nie tylko na uniknięcie prostych błędów rachunkowych czy pomyłek w znakach, ale także buduje Twoją pewność siebie. Kiedy widzisz, że lewa strona równa się prawej, wiesz, że masz rację to bezcenne. Ponadto, regularne sprawdzanie pomaga lepiej zrozumieć koncepcję równości w algebrze, co jest fundamentem dla bardziej zaawansowanych zagadnień. To jak podwójne sprawdzenie, czy dobrze zapakowałeś plecak przed wycieczką daje spokój ducha.

Jak wykonać sprawdzenie równania instrukcja krok po kroku
Aby skutecznie sprawdzić rozwiązanie równania, wystarczy trzymać się kilku prostych zasad. Oto one:
- Zapisz pierwotne równanie: Zawsze zaczynaj od oryginalnej postaci równania, zanim zacząłeś je przekształcać. Dzięki temu masz pewność, że weryfikujesz rozwiązanie dla właściwego problemu.
- Podstaw obliczoną wartość niewiadomej: W miejsce niewiadomej (najczęściej 'x') wstaw wartość, którą obliczyłeś. Pamiętaj, aby być szczególnie ostrożnym, jeśli podstawiasz liczbę ujemną lub ułamek warto wtedy użyć nawiasów, aby uniknąć błędów w kolejności działań lub znakach.
- Oblicz wartość lewej strony równania (L): Wykonaj wszystkie działania po lewej stronie znaku równości, stosując prawidłową kolejność (najpierw nawiasy, potem potęgowanie/pierwiastkowanie, mnożenie/dzielenie, na końcu dodawanie/odejmowanie).
- Oblicz wartość prawej strony równania (P): Analogicznie, wykonaj wszystkie działania po prawej stronie znaku równości, również z zachowaniem prawidłowej kolejności.
- Porównaj wyniki L i P: Jeśli po wszystkich obliczeniach okaże się, że wartość lewej strony (L) jest równa wartości prawej strony (P), oznacza to, że Twoje rozwiązanie jest poprawne. Jeśli wyniki są różne, gdzieś wkradł się błąd.
Przeczytaj również: Czym jest różnica w matematyce? Zrozum odejmowanie bez trudu!
Sprawdzanie na przykładach
Przejdźmy teraz do praktyki. Pokażę Ci, jak zastosować te kroki w różnych typach równań.
Przykład 1: Proste równanie liniowe
Załóżmy, że rozwiązałeś równanie 4x - 5 = 11 i otrzymałeś wynik x = 4. Sprawdźmy to:
- Pierwotne równanie:
4x - 5 = 11 - Podstawiamy
x = 4:4 * 4 - 5 = 11 - Obliczamy lewą stronę (L):
4 * 4 - 5 = 16 - 5 = 11 - Obliczamy prawą stronę (P):
11 - Porównujemy:
L = 11,P = 11. PonieważL = P, rozwiązaniex = 4jest poprawne. Widzisz, jakie to proste?
Przykład 2: Niewiadoma po obu stronach
Rozwiązałeś równanie 3x + 2 = x + 10 i wyszło Ci x = 4. Sprawdźmy, czy to prawda. Podstawiamy x = 4 do obu stron równania: 3 * 4 + 2 = 4 + 10. Teraz obliczamy lewą stronę (L): 12 + 2 = 14. Następnie prawą stronę (P): 4 + 10 = 14. Ponownie, L = P (14 = 14), co oznacza, że rozwiązanie x = 4 jest prawidłowe. W tym przypadku ważne jest, aby podstawić wartość niewiadomej do każdego miejsca, gdzie ona występuje.
Przykład 3: Równanie z ułamkami
Masz równanie ½x + 3 = 5 i obliczyłeś, że x = 4. Sprawdźmy to. Podstawiamy x = 4: ½ * 4 + 3 = 5. Obliczamy lewą stronę (L): ½ * 4 = 2, więc 2 + 3 = 5. Prawa strona (P) to 5. Widzimy, że L = P (5 = 5), więc rozwiązanie jest poprawne. Pamiętaj, aby poprawnie wykonywać działania na ułamkach to częste źródło błędów!
Przykład 4: Równanie z nawiasami
Rozwiązałeś równanie2(x + 3) = 14 i otrzymałeś x = 4. Sprawdźmy. Podstawiamy x = 4: 2(4 + 3) = 14. Teraz kluczowa jest kolejność działań najpierw nawiasy! Obliczamy lewą stronę (L): 2 * (7) = 14. Prawa strona (P) to 14. Ponieważ L = P (14 = 14), rozwiązanie jest poprawne. Zawsze pamiętaj o kolejności działań, szczególnie gdy w grę wchodzą nawiasy.
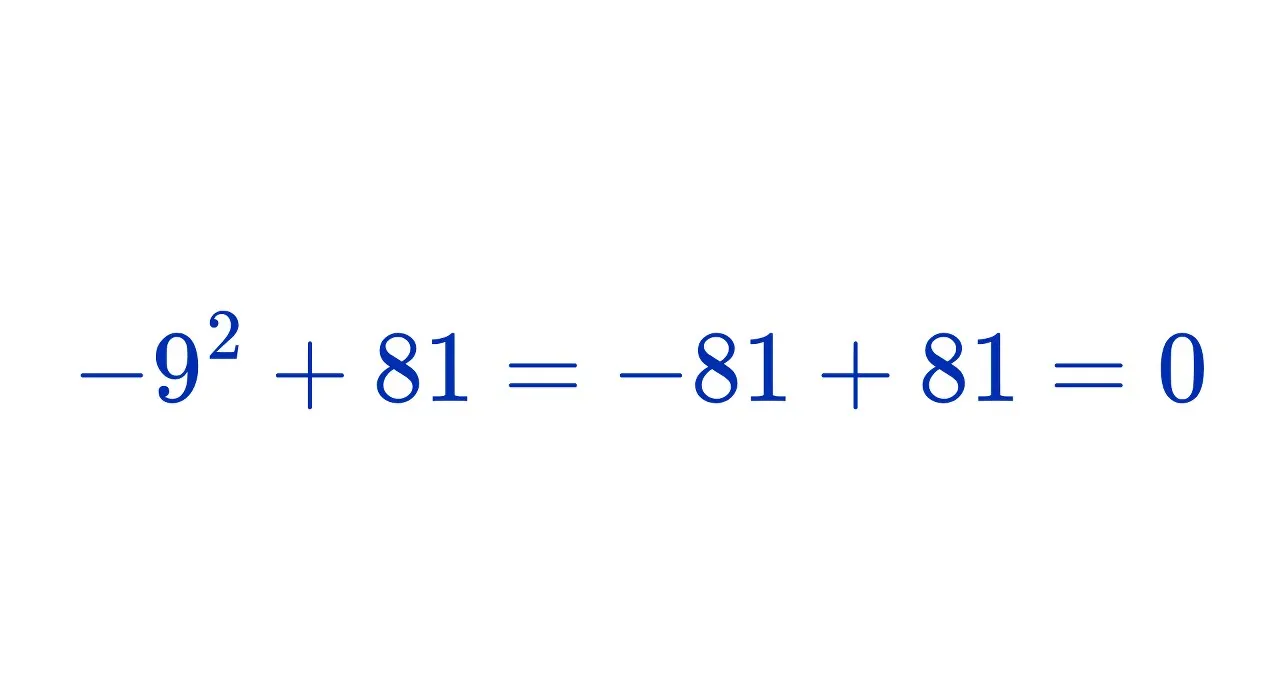
Najczęstsze błędy podczas sprawdzania równań i jak ich unikać
Nawet doświadczeni uczniowie mogą popełniać błędy podczas sprawdzania. Oto lista tych najczęstszych, wraz z moimi radami, jak ich unikać:
-
Gubienie minusów przy podstawianiu liczb ujemnych: To klasyczny błąd. Kiedy podstawiasz liczbę ujemną, np.
x = -2, zawsze używaj nawiasów:2*(-2), a nie2*-2. To pomoże uniknąć pomyłek w znakach. - Zła kolejność wykonywania działań: Pamiętaj o zasadzie "kolejności działań" (nawiasy, potęgi, mnożenie/dzielenie, dodawanie/odejmowanie). Często widzę, jak uczniowie dodają przed mnożeniem, co prowadzi do błędnych wyników.
- Podstawianie wyniku do uproszczonej wersji równania zamiast do oryginalnej: Zawsze, ale to zawsze, podstawiaj wynik do pierwotnego równania. Jeśli podstawisz do wersji, którą już przekształciłeś, możesz nie wykryć błędu popełnionego na wcześniejszym etapie rozwiązywania.
- Pomyłki w obliczeniach na ułamkach: Działania na ułamkach wymagają precyzji. Upewnij się, że poprawnie sprowadzasz do wspólnego mianownika, skracasz czy rozszerzasz. Mały błąd tutaj może zrujnować całe sprawdzenie.
- Niesprawdzenie wszystkich rozwiązań w przypadku równań wielopierwiastkowych: W równaniach kwadratowych czy innych, które mogą mieć więcej niż jedno rozwiązanie, musisz sprawdzić każde z nich osobno. Pamiętaj, że jedno poprawne rozwiązanie nie oznacza, że wszystkie są poprawne.
Co zrobić, jeśli po sprawdzeniu lewa strona nie równa się prawej? To wcale nie jest powód do frustracji, wręcz przeciwnie to cenna informacja! Oznacza to, że gdzieś jest błąd, a Ty masz szansę go znaleźć i poprawić. Najpierw wróć do swojego pierwotnego rozwiązania równania i sprawdź, czy nie popełniono błędu na etapie rozwiązywania może źle przeniosłeś wyraz, pomyliłeś znak, albo źle wykonałeś jakieś działanie. Jeśli tam wszystko wydaje się w porządku, wtedy dokładnie przelicz jeszcze raz samo sprawdzenie, krok po kroku, upewniając się, że nie ma błędów rachunkowych lub pomyłek w kolejności działań. Czasem to właśnie w pośpiechu podczas sprawdzania popełniamy drobne, ale decydujące błędy.
Regularne wykonywanie sprawdzeń to nawyk, który zaprocentuje w przyszłości. Buduje to nie tylko Twoją pewność siebie w obliczu zadań matematycznych, ale także pozwala na samodzielne korygowanie błędów, co jest kluczowe w nauce. Pogłębia to również zrozumienie matematyki, ucząc Cię logicznego myślenia i precyzji. Warto poświęcić te kilka dodatkowych chwil, aby mieć pewność co do swojego wyniku.