W tym praktycznym przewodniku krok po kroku pokażę Ci, jak sprawnie przekształcić równanie prostej z postaci kierunkowej na ogólną. Znajdziesz tu nie tylko niezbędne definicje i wzory, ale także szczegółowo rozwiązane przykłady, w tym te z ułamkami czy liczbami ujemnymi, co czyni go wartościowym narzędziem dla każdego ucznia czy studenta.
Konwersja równania prostej z postaci kierunkowej na ogólną proste kroki i praktyczne przykłady
- Postać kierunkowa to `y = ax + b`, gdzie `a` to współczynnik kierunkowy, a `b` to wyraz wolny.
- Postać ogólna to `Ax + By + C = 0`, która jest uniwersalna i opisuje wszystkie proste, w tym pionowe.
- Główna zasada przekształcania polega na przeniesieniu wszystkich wyrazów równania na jedną stronę, tak aby po drugiej stronie zostało zero.
- Po przeniesieniu wyrazów z `y = ax + b` do `ax - y + b = 0`, współczynniki postaci ogólnej to `A = a`, `B = -1` i `C = b`.
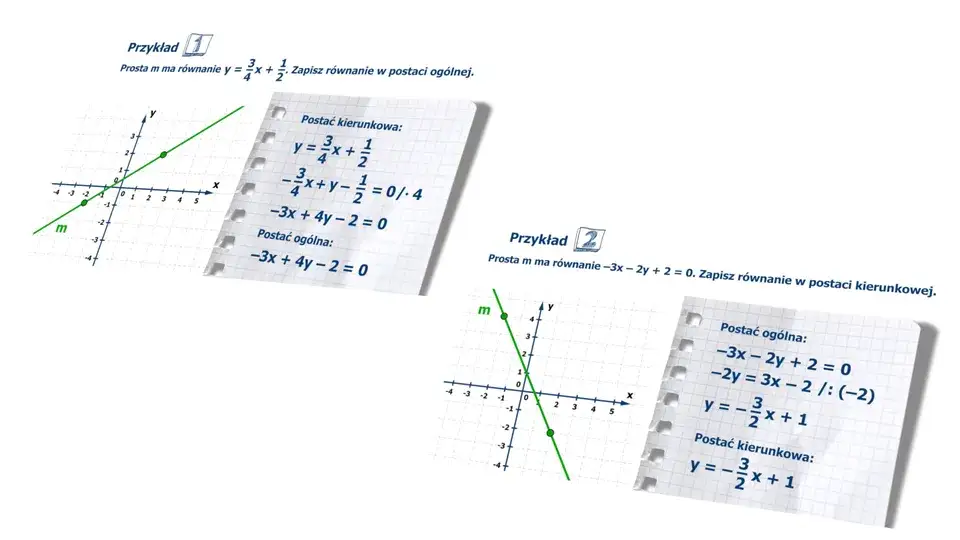
- W przypadku ułamków w równaniu kierunkowym, po przeniesieniu wyrazów, należy pomnożyć całe równanie przez wspólny mianownik, aby uzyskać współczynniki całkowite.
- Postać ogólna jest szczególnie przydatna, ponieważ pozwala opisać proste pionowe (`x = c`), których nie da się przedstawić w postaci kierunkowej.
Dwie twarze równania prostej: postać kierunkowa i ogólna
Zastanawiałeś się kiedyś, dlaczego prostą można opisać na kilka sposobów? To nie przypadek! Różne formy równania prostej służą różnym celom i mają swoje unikalne zalety. Zrozumienie różnic między postacią kierunkową a ogólną jest absolutnie kluczowe dla pełnego opanowania geometrii analitycznej i swobodnego poruszania się po świecie funkcji liniowych.
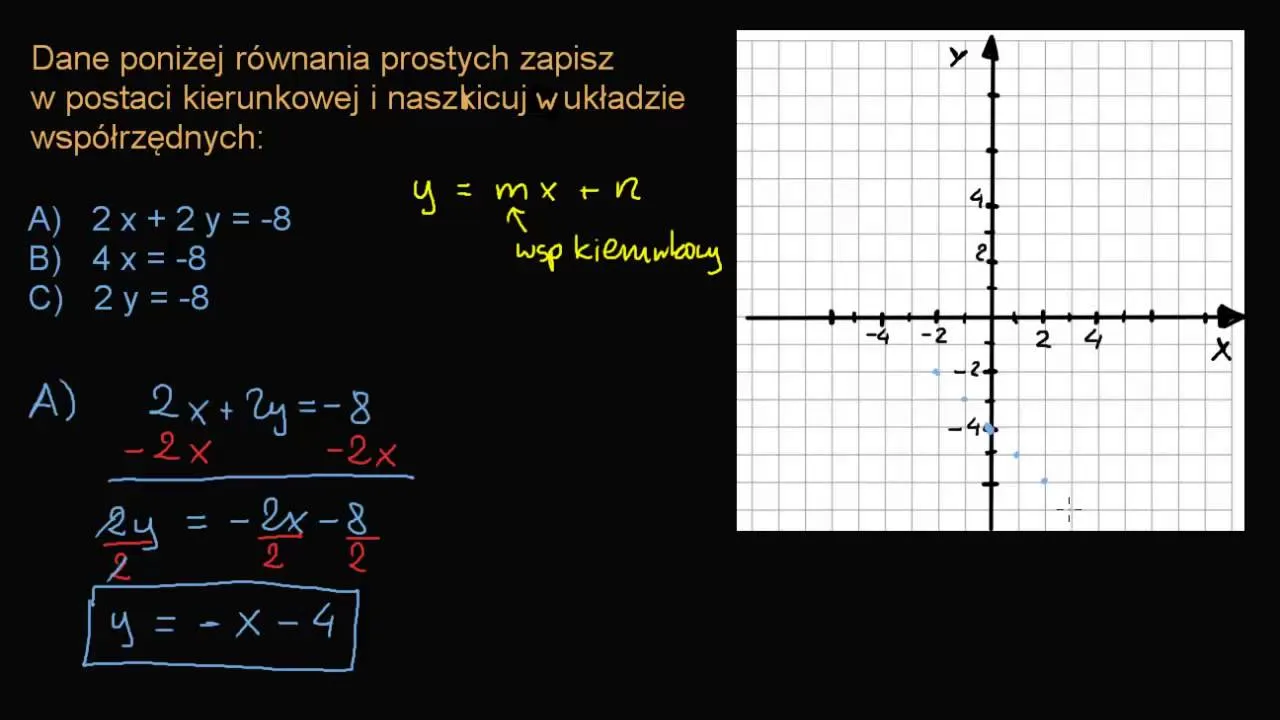
Czym jest postać kierunkowa (y = ax + b)? Szybkie przypomnienie
Postać kierunkowa równania prostej, czyli `y = ax + b`, jest prawdopodobnie tą, którą spotykasz najczęściej. Jest bardzo intuicyjna i łatwa do interpretacji. Współczynnik `a` to nic innego jak współczynnik kierunkowy, który mówi nam o nachyleniu prostej do osi OX. Im większa jego wartość (dodatnia), tym prosta jest "stromsza" i rośnie szybciej. Jeśli `a` jest ujemne, prosta maleje. Z kolei `b` to wyraz wolny, który wskazuje punkt przecięcia prostej z osią OY. To proste jeśli `x = 0`, to `y = b`.
Czym jest postać ogólna (Ax + By + C = 0) i dlaczego jest bardziej uniwersalna?
Postać ogólna równania prostej `Ax + By + C = 0` jest nieco mniej intuicyjna na pierwszy rzut oka, ale za to znacznie bardziej uniwersalna. Kluczowym warunkiem jest to, że współczynniki `A` i `B` nie mogą być jednocześnie równe zeru. Dlaczego jest uniwersalna? Otóż postać kierunkowa ma pewne ograniczenie nie jest w stanie opisać prostych pionowych (równoległych do osi OY), ponieważ ich współczynnik kierunkowy byłby nieskończony. Postać ogólna radzi sobie z tym bez problemu, co czyni ją niezastąpioną w wielu sytuacjach.
Kiedy jedna forma jest lepsza od drugiej? Praktyczne zastosowania
Jako Alan Szymczak, zawsze podkreślam, że wybór odpowiedniej formy równania zależy od kontekstu zadania. Obie mają swoje mocne strony:
-
Postać kierunkowa (`y = ax + b`):
- Jest idealna do szybkiego rysowania wykresu prostej, ponieważ od razu widzimy punkt przecięcia z osią OY (`b`) i nachylenie (`a`).
- Ułatwia analizę, czy prosta jest rosnąca, malejąca czy stała.
- Jest często wykorzystywana w funkcjach liniowych i ich zastosowaniach.
-
Postać ogólna (`Ax + By + C = 0`):
- Jej główna przewaga to uniwersalność pozwala opisać wszystkie proste, w tym te pionowe, które są niemożliwe do przedstawienia w postaci kierunkowej.
- Jest często używana w bardziej zaawansowanych obliczeniach geometrii analitycznej, np. do wyznaczania odległości punktu od prostej czy kąta między prostymi.
- Upraszcza pewne operacje, gdy nie musimy martwić się o nieskończone nachylenia.
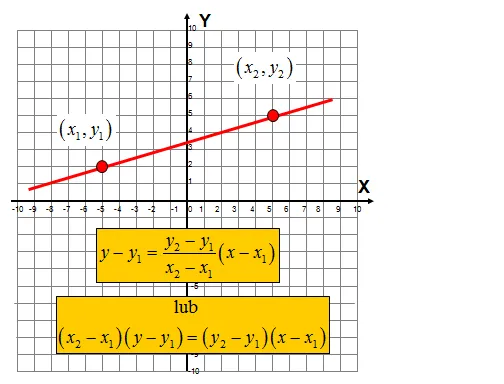
Przekształcanie krok po kroku: od postaci kierunkowej do ogólnej
Przekształcanie równania prostej z postaci kierunkowej na ogólną to naprawdę prosty proces, który wymaga jedynie kilku podstawowych kroków. Nie ma tu żadnej magii, tylko konsekwentne stosowanie zasad algebry. Zaraz Ci pokażę, jak to zrobić.
Główna zasada: przenieś wszystko na jedną stronę, by uzyskać zero
Kluczem do sukcesu jest przeniesienie wszystkich wyrazów z równania kierunkowego `y = ax + b` na jedną stronę, tak aby po drugiej stronie zostało zero. Standardowo, dążymy do tego, aby współczynnik przy `x` był dodatni, ale nie jest to bezwzględnie konieczne. Zobaczmy na przykładzie ogólnym:
Zaczynamy od: `y = ax + b`
Przenosimy `y` na prawą stronę (lub `ax` i `b` na lewą), pamiętając o zmianie znaku:
`0 = ax - y + b`
Następnie, dla czytelności i zgodności z konwencją, zapisujemy to w kolejności `Ax + By + C = 0`:
`ax - y + b = 0`
I to już jest postać ogólna! Proste, prawda?
Jak zidentyfikować współczynniki A, B i C w nowym równaniu?
Gdy już przekształcimy równanie do formy `ax - y + b = 0`, odczytanie współczynników `A`, `B` i `C` dla postaci ogólnej `Ax + By + C = 0` jest banalnie proste. Wystarczy porównać oba równania:
- `A` to współczynnik przy `x`, więc `A = a`.
- `B` to współczynnik przy `y`. Ponieważ `y` zostało przeniesione ze zmienionym znakiem, mamy `-y`, co oznacza, że `B = -1`.
- `C` to wyraz wolny, czyli `C = b`.
Widzisz, to jest naprawdę bezpośrednie przełożenie.
Wzór, który upraszcza wszystko: jak `a` i `b` zamieniają się w `A`, `B` i `C`
Podsumowując, możemy zapamiętać proste zależności między współczynnikami postaci kierunkowej (`a`, `b`) a ogólnej (`A`, `B`, `C`) dla standardowego przekształcenia:
Jeśli masz `y = ax + b`, to po przekształceniu do `ax - y + b = 0` otrzymujesz:
- `A = a`
- `B = -1`
- `C = b`
Warto pamiętać, że równanie w postaci ogólnej nie jest unikalne. Oznacza to, że możesz pomnożyć całe równanie przez dowolną liczbę różną od zera, a nadal będzie ono opisywać tę samą prostą. Na przykład, `2x - y + 5 = 0` opisuje tę samą prostą co `-2x + y - 5 = 0`. Jednak forma `ax - y + b = 0` jest standardowym i najprostszym punktem wyjścia.
Praktyka czyni mistrza: rozwiązujemy typowe przykłady
Teoria to jedno, ale prawdziwe zrozumienie przychodzi z praktyką. Dlatego przygotowałem dla Ciebie kilka szczegółowo rozwiązanych przykładów. Przejdziemy przez klasyczne równania, te z ułamkami, a także z liczbami ujemnymi, abyś poczuł się pewnie w każdej sytuacji.
Przykład 1: Klasyczne równanie z liczbami całkowitymi
Zacznijmy od prostego przykładu z liczbami całkowitymi: `y = 2x + 3`.
-
Krok 1: Przenosimy wyrazy z prawej strony na lewą
Naszym celem jest, aby po prawej stronie równania zostało zero. Przenosimy `2x` i `3` na lewą stronę, pamiętając o zmianie znaków:
`y - 2x - 3 = 0`
-
Krok 2: Porządkujemy zapis do formy Ax + By + C = 0
Dla czytelności i zgodności z konwencją, zmieniamy kolejność wyrazów na `x`, `y`, `liczba stała`:
`-2x + y - 3 = 0`
Opcjonalnie, możemy pomnożyć całe równanie przez -1, aby współczynnik `A` był dodatni (co jest często preferowane):
`2x - y + 3 = 0`
-
Krok 3: Odczytujemy finalne współczynniki
Z równania `2x - y + 3 = 0` łatwo odczytujemy:
- `A = 2`
- `B = -1`
- `C = 3`
Przykład 2: Jak poradzić sobie z ułamkami w równaniu?
Ułamki często sprawiają kłopoty, ale z moimi wskazówkami poradzisz sobie z nimi bez problemu. Weźmy równanie: `y = (2/3)x + 1/2`.
-
Krok 1: Standardowe przeniesienie wyrazów
Jak poprzednio, przenosimy wszystkie wyrazy na jedną stronę, zmieniając ich znaki:
`(2/3)x - y + 1/2 = 0`
-
Krok 2: Kluczowy ruch mnożenie przez wspólny mianownik
Aby pozbyć się ułamków i uzyskać współczynniki całkowite (co jest standardową i zalecaną praktyką w postaci ogólnej), musimy pomnożyć całe równanie przez wspólny mianownik wszystkich ułamków. W tym przypadku mianowniki to 3 i 2, więc wspólnym mianownikiem jest 6.
Mnożymy każdy wyraz przez 6:
`6 * (2/3)x - 6 * y + 6 * (1/2) = 6 * 0`
`4x - 6y + 3 = 0`
-
Krok 3: Prezentacja ostatecznego równania z liczbami całkowitymi
Z równania `4x - 6y + 3 = 0` odczytujemy:
- `A = 4`
- `B = -6`
- `C = 3`
Przykład 3: Co zrobić, gdy współczynniki są ujemne?
Liczby ujemne nie powinny Cię zaskoczyć. Proces jest identyczny. Rozważmy: `y = -3x - 5`.
-
Krok 1: Przenosimy wyrazy z prawej strony na lewą
Przenosimy `-3x` i `-5` na lewą stronę, zmieniając ich znaki:
`y + 3x + 5 = 0`
-
Krok 2: Porządkujemy zapis do formy Ax + By + C = 0
Uporządkujmy wyrazy w standardowej kolejności:
`3x + y + 5 = 0`
W tym przypadku współczynnik `A` jest już dodatni, więc nie ma potrzeby mnożenia przez -1. Gdybyśmy mieli np. `-3x - y - 5 = 0`, moglibyśmy pomnożyć przez -1, aby uzyskać `3x + y + 5 = 0`. Obie formy są poprawne i opisują tę samą prostą.
-
Krok 3: Odczytujemy finalne współczynniki
Z równania `3x + y + 5 = 0` odczytujemy:
- `A = 3`
- `B = 1`
- `C = 5`
Nietypowe przypadki: proste poziome i pionowe
W geometrii analitycznej istnieją szczególne typy prostych, które wymagają nieco innej uwagi podczas przekształcania. Zrozumienie ich jest kluczowe dla pełnego obrazu i uniknięcia nieporozumień.
Jak przekształcić równanie prostej poziomej (y = c)?
Prosta pozioma to taka, która jest równoległa do osi OX. Jej równanie w postaci kierunkowej to po prostu `y = b`, gdzie `b` jest stałą (współczynnik kierunkowy `a` wynosi 0). Przekształcenie jej do postaci ogólnej jest bardzo proste:
Zaczynamy od: `y = b`
Przenosimy `b` na lewą stronę:
`y - b = 0`
W tej formie, porównując z `Ax + By + C = 0`, widzimy, że:
- `A = 0` (nie ma wyrazu z `x`)
- `B = 1` (współczynnik przy `y`)
- `C = -b`
Dlaczego prostej pionowej (x = c) nie da się zapisać w postaci kierunkowej?
Prosta pionowa to prosta równoległa do osi OY. Jej równanie ma postać `x = c`, gdzie `c` jest stałą. Taka prosta ma nieskończone nachylenie, co oznacza, że nie da się jej przedstawić w postaci kierunkowej `y = ax + b`. To właśnie tutaj postać ogólna pokazuje swoją prawdziwą uniwersalność.
Przekształcenie `x = c` do postaci ogólnej jest równie proste:
Zaczynamy od: `x = c`
Przenosimy `c` na lewą stronę:
`x - c = 0`
Porównując z `Ax + By + C = 0`, odczytujemy współczynniki:
- `A = 1` (współczynnik przy `x`)
- `B = 0` (nie ma wyrazu z `y`)
- `C = -c`
Zrozumienie tego ograniczenia postaci kierunkowej jest bardzo ważne dla pełnego kontekstu i świadomego wyboru odpowiedniej formy równania.
Unikaj najczęstszych błędów: sprawdź, zanim oddasz zadanie
Nawet najlepsi popełniają błędy, ale jako Alan Szymczak, zawsze powtarzam, że świadomość typowych pułapek pozwala ich unikać. Sprawdź te punkty, zanim oddasz swoje zadanie, a zminimalizujesz ryzyko pomyłek.
Pomyłki w znakach przy przenoszeniu wyrazów
To chyba najczęstszy błąd, jaki widzę u moich uczniów. Zapominanie o zmianie znaku wyrazu przenoszonego na drugą stronę równania to klasyka gatunku. Pamiętaj: jeśli przenosisz wyraz z jednej strony równania na drugą, zawsze musisz zmienić jego znak na przeciwny. To podstawowa zasada algebry, ale w pośpiechu łatwo o niej zapomnieć.
Zapominanie o uporządkowaniu równania do standardowej kolejności (x, y, liczba)
Choć matematycznie kolejność wyrazów w równaniu ogólnym nie wpływa na jego poprawność, to dla jasności, łatwego odczytywania współczynników i zgodności z matematycznymi konwencjami, zawsze dążymy do formy `Ax + By + C = 0`. Upewnij się, że Twoje równanie ma najpierw wyraz z `x`, potem z `y`, a na końcu wyraz stały.
Przeczytaj również: Dzielna i dzielnik: Jak je odróżnić? Proste triki i przykłady!
Pozostawianie ułamków w ostatecznej postaci ogólnej
Jak już wspomniałem przy przykładzie z ułamkami, standardową i zalecaną praktyką jest pozbywanie się ułamków z równania w postaci ogólnej. Osiągamy to poprzez pomnożenie całego równania przez wspólny mianownik. Dzięki temu współczynniki `A`, `B` i `C` są liczbami całkowitymi, co jest bardziej estetyczne i często ułatwia dalsze obliczenia.